
- •Глава 8 ряды фурье
- •§1. Ортонормированные системы и общие ряды фурье
- •§2. Замкнутые и полные ортонормированные системы
- •§3. Замкнутость тригонометрической системы и следствия из нее
- •3. Следствия замкнутости тригонометрической системы.
- •§4. Простейшие условия равномерной сходимости и почленного дифференцирования тригонометрического ряда фурье
- •2. Простейшие условия абсолютной и равномерной сходимости тригонометрического ряда Фурье.
- •§5. Более точные условия равномерной сходимости и условия сходимости в данной точке
- •3. Вспомогательные предложения.
3. Вспомогательные предложения.
Лемма.
Пусть
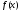 кусочно
непрерывная на сегменте
кусочно
непрерывная на сегменте
 и
периодически с периодом
и
периодически с периодом
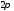 продолжена
на всю бесконечную прямую. Тогда для
любого
продолжена
на всю бесконечную прямую. Тогда для
любого
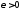 найдется
такое
найдется
такое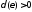 ,
что при всех
,
что при всех ,
удовлетворяющих условию
,
удовлетворяющих условию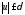 ,
справедливо неравенство
,
справедливо неравенство
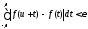 .
.
Доказательство.
Фиксируем произвольное
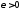 .
Согласно теореме 8.8 (о замкнутости
тригонометрической системы) для функции
.
Согласно теореме 8.8 (о замкнутости
тригонометрической системы) для функции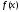 найдется
тригонометрический многочлен
найдется
тригонометрический многочлен
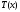 такой,
что
такой,
что
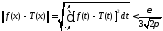 ,
,
и
потому на основании неравенства
Коши-Буняковского20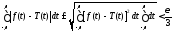 .
(8.56)
.
(8.56)
Из
неравенства (8.56), из леммы п. 2 и из того,
что
 и
и являются
периодическими функциями периода
являются
периодическими функциями периода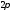 ,
заключаем, что для любого числа
,
заключаем, что для любого числа
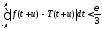 .
(8.57)
.
(8.57)
Поскольку
модуль суммы трех величин не превосходит
сумму модулей этих величин, то для любого
числа
 справедливо неравенство
справедливо неравенство
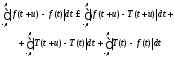 .
(8.58)
.
(8.58)
Теперь
остается заметить, что в силу непрерывности
тригонометрического многочлена и
теоремы Кантора (см. теорему 4.16 ч.1) для
фиксированного нами
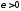 найдется
найдется
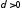 такое,
что при
такое,
что при
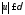 и
и
 при
всех из
при
всех из
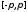
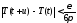
и потому
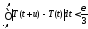 .
(8.59)
.
(8.59)
Сопоставляя неравенство (8.58) с неравенствами (8.56), (8.57) и (8.59), получим
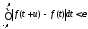 (8.60)
(8.60)
для
всех
 ,
для которых
,
для которых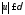 .
Лемма доказана.
.
Лемма доказана.
Извлечем теперь из этой леммы ряд важных для дальнейшего следствий.
Следствие
1. Если функция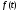 кусочно непрерывна на сегменте
кусочно непрерывна на сегменте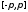 и периодически (с периодом
и периодически (с периодом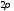 )
продолжена на всю бесконечную прямую,
а
)
продолжена на всю бесконечную прямую,
а - любая фиксированная точка сегмента
- любая фиксированная точка сегмента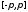 ,
то для любого
,
то для любого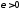 найдется
найдется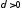 такое,
что
такое,
что
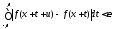 (8.61)
(8.61)
при
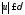 .
.
Доказательство.
Сделаем в интеграле, стоящем в левой
части (8.61), замену переменной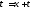 :
:
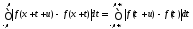 .
.
В силу равенства (8.49)
 .
.
Следовательно, неравенство (8.61) является следствием (8.60).
Следствие
2. Если каждая из функций
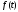 и
и
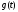 кусочно
непрерывна на сегменте
кусочно
непрерывна на сегменте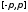 и
периодически (с периодом
и
периодически (с периодом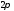 )
продолжена на всю прямую, то функция
)
продолжена на всю прямую, то функция
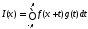
является
непрерывной функцией
 на
сегменте
на
сегменте
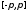 .
.
Доказательство.
Пусть
 - любая точка сегмента
- любая точка сегмента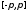 .
Тогда
.
Тогда
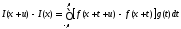 ,
,
и
поскольку кусочно непрерывная на
сегменте
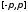 функция
функция
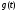 удовлетворяет
на этом сегменте условию ограниченности
удовлетворяет
на этом сегменте условию ограниченности
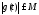 ,
то
,
то
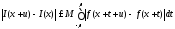 ,
,
и
потому в силу (8.61) для любого
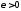
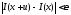 при
при
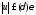 .
.
Непрерывность
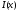 в
точке
в
точке
 доказана.
доказана.
Следствие
3.
Если
каждая из функций
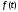 и
и
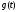 кусочно
непрерывна на сегменте
кусочно
непрерывна на сегменте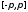 и
периодически (с периодом
и
периодически (с периодом
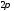 )
продолжена на всю прямую, то
тригонометрические коэффициенты Фурье
функции
)
продолжена на всю прямую, то
тригонометрические коэффициенты Фурье
функции при разложении ее по переменной
при разложении ее по переменной
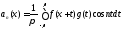 ,
(8.62)
,
(8.62)
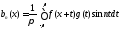 (8.63)
(8.63)
при
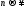 сходятся к нулю равномерно относительно
сходятся к нулю равномерно относительно на
сегменте
на
сегменте
 (а, следовательно, и на всей прямой).
(а, следовательно, и на всей прямой).
Доказательство.
Для любой фиксированной точки
 сегмента
сегмента
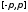 функция
функция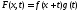 является кусочно непрерывной функцией
аргумента
является кусочно непрерывной функцией
аргумента на
сегменте
на
сегменте
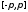 ,
поэтому для нее справедливо равенство
Парсеваля21
,
поэтому для нее справедливо равенство
Парсеваля21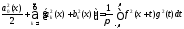 .
(8.64)
.
(8.64)
Из
равенства (8.64) вытекает сходимость ряда,
стоящего в левой его части, в каждой
фиксированной точке
 сегмента
сегмента
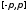 .
Так как указанный ряд состоит изнеотрицательных
членов, то в силу теоремы Дини22для доказательства равномерной на
сегменте
.
Так как указанный ряд состоит изнеотрицательных
членов, то в силу теоремы Дини22для доказательства равномерной на
сегменте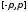 сходимости
указанного ряда достаточно доказать,
что как функции
сходимости
указанного ряда достаточно доказать,
что как функции
 и
и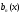 ,
так и сумма ряда (8.64)
,
так и сумма ряда (8.64)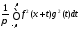 -
непрерывная функция
-
непрерывная функция на
сегменте
на
сегменте
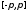 ,
а это сразу вытекает из предыдущего
следствия (достаточно учесть, что квадрат
кусочно непрерывной функции является
кусочно непрерывной функцией и что
,
а это сразу вытекает из предыдущего
следствия (достаточно учесть, что квадрат
кусочно непрерывной функции является
кусочно непрерывной функцией и что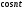 и
и
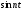 при
каждом фиксированном номере n
являются непрерывными функциями).
Следствие 4. Если каждая из функций
при
каждом фиксированном номере n
являются непрерывными функциями).
Следствие 4. Если каждая из функций
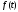 и
и
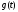 кусочно
непрерывна на сегменте
кусочно
непрерывна на сегменте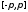 и
периодически с периодом
и
периодически с периодом
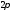 продолжена на всю прямую, то
последовательность
продолжена на всю прямую, то
последовательность
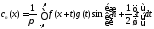 (8.65)
(8.65)
сходится
к нулю равномерно относительно
 на
сегменте
на
сегменте
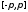 (а следовательно, и на всей прямой).
(а следовательно, и на всей прямой).
Доказательство. Достаточно учесть, что
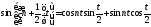
и
применить предыдущее следствие, беря
в (8.62) вместо
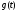 функцию
функцию
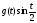 ,
а в (8.63) вместо
,
а в (8.63) вместо функцию
функцию
 .
.
4.
Принцип локализации.
В этом пункте мы докажем, что вопрос о
том, сходится или расходится
тригонометрический ряд Фурье кусочно
непрерывной на сегменте
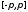 и
периодической (с периодом
и
периодической (с периодом
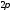 )
функции
)
функции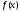 в
данной точке
в
данной точке
 ,
решается лишь на основании поведения
функции
,
решается лишь на основании поведения
функции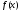 в
как угодно малой окрестности точки
в
как угодно малой окрестности точки
 .
Это замечательное свойство
тригонометрического ряда Фурье принято
называтьпринципом
локализации.
.
Это замечательное свойство
тригонометрического ряда Фурье принято
называтьпринципом
локализации.
Начнем с доказательства важной леммы.
Лемма
(лемма Римана). Если функция
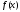 кусочно
непрерывна на сегменте
кусочно
непрерывна на сегменте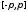 и периодически (с периодом
и периодически (с периодом
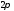 )
продолжена на всю прямую и если эта
функция обращается в нуль на некотором
сегменте
)
продолжена на всю прямую и если эта
функция обращается в нуль на некотором
сегменте 23,
то для любого положительного числа
23,
то для любого положительного числа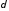 ,
меньшего
,
меньшего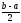 ,
тригонометрический ряд Фурье функции
,
тригонометрический ряд Фурье функции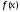 равномерно
на сегменте
равномерно
на сегменте
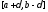 сходится к нулю.Доказательство.
Пусть
сходится к нулю.Доказательство.
Пусть
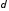 - произвольное положительное число,
меньшее
- произвольное положительное число,
меньшее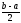 .
Частичная сумма тригонометрического
ряда Фурье функции
.
Частичная сумма тригонометрического
ряда Фурье функции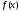 в
произвольной точке
в
произвольной точке
 числовой
прямой определяется равенством (8.54).
Полагая
числовой
прямой определяется равенством (8.54).
Полагая
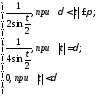 (8.65)
(8.65)
и
учитывая, что
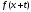 равняется
нулю при условии, что
равняется
нулю при условии, что
 принадлежит
сегменту
принадлежит
сегменту
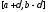 ,
а
,
а принадлежит
сегменту
принадлежит
сегменту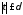 24,
можно следующим образом переписать
равенство (8.54) для каждой точки
24,
можно следующим образом переписать
равенство (8.54) для каждой точки сегмента
сегмента
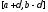 :
: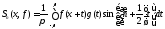 .
.
Остается принять во внимание, что последовательность, стоящая в правой части последнего равенства, в силу следствия 4 п. 3 сходится к нулю равномерно
относительно на всей числовой прямой. Лемма доказана.
на всей числовой прямой. Лемма доказана.
Непосредственными следствиями доказанной леммы являются следующие две теоремы.
Теорема
8.11. Пусть функция
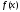 кусочно
непрерывна на сегменте
кусочно
непрерывна на сегменте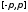 и периодически (с периодом
и периодически (с периодом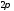 )
продолжена на всю прямую, и пусть
)
продолжена на всю прямую, и пусть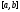 - некоторый сегмент. Для того, чтобы
тригонометрический ряд Фурье функции
- некоторый сегмент. Для того, чтобы
тригонометрический ряд Фурье функции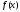 при любом положительном
при любом положительном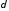 , меньшем
, меньшем , сходился (к этой функции) равномерно
на сегменте
, сходился (к этой функции) равномерно
на сегменте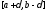 ,
достаточно чтобы существовала кусочно
непрерывная на сегменте
,
достаточно чтобы существовала кусочно
непрерывная на сегменте и периодическая (с периодом
и периодическая (с периодом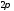 )функция
)функция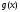 ,
обладающая равномерно сходящимся на
сегменте
,
обладающая равномерно сходящимся на
сегменте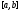 тригонометрическим рядом Фурье и
совпадающая на сегменте
тригонометрическим рядом Фурье и
совпадающая на сегменте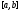 с
функцией
с
функцией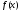 .
.
Доказательство.
Применяя лемму Римана к разности
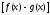 ,
получим, что тригонометрический ряд
Фурье разности
,
получим, что тригонометрический ряд
Фурье разности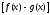 при
любом
при
любом
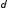 из
интервала
из
интервала
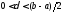 сходится
к нулю равномерно на сегменте
сходится
к нулю равномерно на сегменте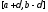 ,
а отсюда и из равномерной на сегменте
,
а отсюда и из равномерной на сегменте сходимости тригонометрического ряда
Фурье функции
сходимости тригонометрического ряда
Фурье функции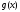 вытекает
равномерная на сегменте
вытекает
равномерная на сегменте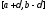 сходимость тригонометрического ряда
Фурье функции
сходимость тригонометрического ряда
Фурье функции
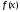 .
Тот факт, что последний ряд сходится на
сегменте
.
Тот факт, что последний ряд сходится на
сегменте именно
к функции
именно
к функции
 ,
непосредственно вытекает из следствия
5 п. 3 § 3. Теорема доказана.
,
непосредственно вытекает из следствия
5 п. 3 § 3. Теорема доказана.
Теорема
8.12.
Пусть
функция
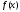 кусочно
непрерывна на сегменте
кусочно
непрерывна на сегменте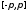 и периодически (с периодом
и периодически (с периодом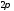 )
продолжена на всю прямую, и пусть
)
продолжена на всю прямую, и пусть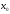 некоторая точка прямой. Для того, чтобы
тригонометрический ряд Фурье функции
некоторая точка прямой. Для того, чтобы
тригонометрический ряд Фурье функции
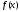 сходился
в точке
сходился
в точке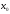 ,достаточно, чтобы существовала кусочно
непрерывная на сегменте
,достаточно, чтобы существовала кусочно
непрерывная на сегменте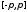 и
периодическая (с периодом
и
периодическая (с периодом
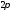 )
функция
)
функция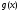 ,
обладающая сходящимся в точке
,
обладающая сходящимся в точке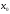 тригонометрическим
рядом Фурье и совпадающая с
тригонометрическим
рядом Фурье и совпадающая с
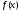 в
как угодной малой
в
как угодной малой
 –
окрестности точки
–
окрестности точки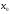 .
.
Доказательство.
Достаточно применить лемму Римана к
разности
 по
сегменту
по
сегменту
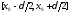 и
учесть что из сходимости в точке
и
учесть что из сходимости в точке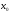 тригонометрических
рядов функций
тригонометрических
рядов функций
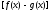 и
и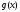 вытекает
сходимость в этой точке и тригонометрического
ряда Фурье функции
вытекает
сходимость в этой точке и тригонометрического
ряда Фурье функции .
Теорема доказана.
.
Теорема доказана.
Теорема
8.12 не устанавливает конкретного вида
условий, обеспечивающих сходимость
тригонометрического ряда Фурье функции
 в
точке
в
точке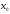 .
Она лишь доказывает, что эти условия
определяются только поведением
.
Она лишь доказывает, что эти условия
определяются только поведением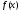 в
как угодно малой окрестности точки
в
как угодно малой окрестности точки
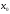 (т.е. имеютлокальный
характер).
(т.е. имеютлокальный
характер).
5.
Равномерная сходимость тригонометрического
ряда Фурье для функции из класса Гёльдера.
В этом и следующем пункте мы уточним
условия, обеспечивающие равномерную
сходимость и сходимость в данной точке
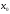 тригонометрического
ряда Фурье.
тригонометрического
ряда Фурье.
Теорема
8.13. Если функция
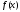 принадлежит на сегменте
принадлежит на сегменте классу
Гёльдера
классу
Гёльдера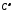 с
каким угодно положительным показателем
с
каким угодно положительным показателем
 (
(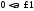 )
и если, кроме того,
)
и если, кроме того, ,
то тригонометрический ряд Фурье функции
,
то тригонометрический ряд Фурье функции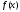 сходится
(к этой функции) равномерно на сегменте
сходится
(к этой функции) равномерно на сегменте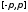 .
.
11 Т.е. в каждой точке разрыва у функции существует конечный левый и конечный правый пределы.
2 Для доказательства неравенства (8.3) заметим, что для любого вещественного в силу аксиомы 40 скалярного произведения справедливо неравенство , которое в силу аксиом 10 – 40 эквивалентно неравенству . Необходимым и достаточным условием неотрицательности квадратного трехчлена, стоящего в левой части последнего неравенства, является неположительность его дискриминанта, т.е. неравенство, которое эквивалентно неравенству (8.3).
3 Фридрих Вильгельм Бессель – немецкий астроном и математик (1784-1846).
4 М.А.Парсеваль – французский математик (1755-1836).
5 Под тригонометрическими функциями в данном случае понимаются косинус и синус.
6 Так как эта функция удовлетворяет тем же условиям, что и полученная после продолжения функция .
7 А следовательно (в силу теоремы 8.5), и полной
8 Первый пример такой функции был построен французским математиком Дю Буа Раймоном в 1876г.
9При этом функция может оказаться неопределенной в конечном числе точек сегмента. В этих точках мы доопределим ее произвольным образом (например, положим равной полусумме правого и левого предельных значений).
10Например, можно положить функцию в указанных точках равной полусумме правого и левого предельных значений.
11При интегрировании по частям следует разбить сегмент на конечное число не имеющих общих вну
12
13
14
15
16
17
18
19
20
21
22
23
24
