
- •Глава 8 ряды фурье
- •§1. Ортонормированные системы и общие ряды фурье
- •§2. Замкнутые и полные ортонормированные системы
- •§3. Замкнутость тригонометрической системы и следствия из нее
- •3. Следствия замкнутости тригонометрической системы.
- •§4. Простейшие условия равномерной сходимости и почленного дифференцирования тригонометрического ряда фурье
- •2. Простейшие условия абсолютной и равномерной сходимости тригонометрического ряда Фурье.
- •§5. Более точные условия равномерной сходимости и условия сходимости в данной точке
- •3. Вспомогательные предложения.
§3. Замкнутость тригонометрической системы и следствия из нее
1.
Равномерное приближение непрерывной
функции тригонометрическими многочленами.
В этом параграфе будет установлена
замкнутость (а следовательно, и полнота)
тригонометрической системы (8.10) в
пространстве всех кусочно непрерывных
на сегменте
 функций.
Но прежде чем приступить к доказательству
замкнутости тригонометрической системы,
установим важную теорему о равномерном
приближении непрерывной функции так
называемыми тригонометрическими
многочленами.
функций.
Но прежде чем приступить к доказательству
замкнутости тригонометрической системы,
установим важную теорему о равномерном
приближении непрерывной функции так
называемыми тригонометрическими
многочленами.
Будем называть тригонометрическим многочленом произвольную линейную комбинацию любого конечного числа элементов тригонометрической системы (8.10), т.е. выражение вида
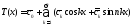 ,
,
где
n
– любой номер, а
 ,
, и
и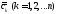 - произвольные постоянные вещественные
числа.
- произвольные постоянные вещественные
числа.
Отметим два совершенно элементарных утверждения:
10.
Если
 - какой угодно алгебраический многочлен
произвольной степениn,
то
- какой угодно алгебраический многочлен
произвольной степениn,
то
 и
и
 -
тригонометрические многочлены.
-
тригонометрические многочлены.
20.
Если
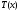 -
тригонометрический многочлен, то каждое
из выражений
-
тригонометрический многочлен, то каждое
из выражений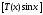 и
и также
представляет собой тригонометрический
многочлен.
также
представляет собой тригонометрический
многочлен.
Оба
утверждения вытекают из того, что
произведение двух (а поэтому и любого
конечного числа) тригонометрических
функций5от аргумента приводится к
приводится к
линейной
комбинации конечного числа тригонометрических
функций от аргументов типа
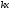 (убедитесь в этом сами).
(убедитесь в этом сами).
В теории тригонометрических рядов Фурье важную роль играет понятие периодической функции.
Определение.
Функция
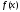 ,
определенная для всех вещественных
,
определенная для всех вещественных называется
периодической с периодом Т, если для
любого вещественного
называется
периодической с периодом Т, если для
любого вещественного
 справедливо
равенство
справедливо
равенство
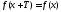 .
.
Это равенство обычно называется условием периодичности. К рассмотрению периодических функций приводит изучение различных колебательных процессов.
Заметим,
что все элементы тригонометрической
системы (8.10) являются периодическими
функциями с периодом
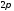 .
.
Теорема
8.7 (теорема Вейерштрасса). Если функция
 непрерывна
на сегменте
непрерывна
на сегменте
 и
удовлетворяет условию
и
удовлетворяет условию
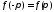 ,
то эту функцию можно равномерно на
указанном сегменте приблизить
тригонометрическими многочленами, т.е.
для этой функции
,
то эту функцию можно равномерно на
указанном сегменте приблизить
тригонометрическими многочленами, т.е.
для этой функции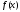 и
для любого положительного числа
и
для любого положительного числа
 найдется
тригонометрический многочлен
найдется
тригонометрический многочлен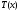 такой,
что сразу для всех
такой,
что сразу для всех
 из
сегмента
из
сегмента
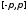 справедливо
неравенство
справедливо
неравенство
 .
(8.26)
.
(8.26)
Доказательство. Для удобства разобьем доказательство на два этапа.
1)
Сначала дополнительно предположим, что
функция
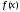 является
четной,
т.е. для любого
является
четной,
т.е. для любого
 из
сегмента
из
сегмента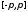 удовлетворяет условию
удовлетворяет условию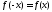 .
.
В
силу теоремы о непрерывности сложной
функции
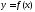 ,
где
,
где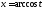 (см. §1 гл. 4 ч. 1) функция
(см. §1 гл. 4 ч. 1) функция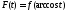 является
непрерывной функцией аргумента
является
непрерывной функцией аргумента
 на
сегменте
на
сегменте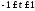 .
Следовательно, по теореме Вейерштрасса
для алгебраических многочленов (см.
теорему 2.18) для любого
.
Следовательно, по теореме Вейерштрасса
для алгебраических многочленов (см.
теорему 2.18) для любого найдется
алгебраический многочлен
найдется
алгебраический многочлен такой,
что
такой,
что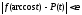 сразу
для всех
сразу
для всех
 из
сегмента
из
сегмента
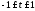 .
.
Положив
 ,
мы получим
,
мы получим
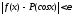 (8.27)
(8.27)
сразу
для всех
 из
сегмента
из
сегмента
 .
.
Так
как обе функции
 и
и
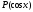 являются
четными, то неравенство (8.27) справедливо
и для всех
являются
четными, то неравенство (8.27) справедливо
и для всех
 из
сегмента
из
сегмента
 .
Таким образом, неравенство (8.27) справедливо
для всех
.
Таким образом, неравенство (8.27) справедливо
для всех из
сегмента
из
сегмента
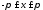 ,
и поскольку (в силу указанного выше
утверждения 10)
,
и поскольку (в силу указанного выше
утверждения 10)
 является
тригонометрическим многочленом, то для
четной функции
является
тригонометрическим многочленом, то для
четной функции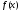 теорема
доказана.
теорема
доказана.
Заметим
теперь, что функцию
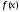 ,
удовлетворяющую условиям доказываемой
теоремы, можно периодически с периодом
,
удовлетворяющую условиям доказываемой
теоремы, можно периодически с периодом продолжить на всю бесконечную прямую
продолжить на всю бесконечную прямую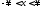 ,
так что продолженная функция будет
непрерывной в каждой точке
,
так что продолженная функция будет
непрерывной в каждой точке бесконечной
прямой. Кроме того, если функция
бесконечной
прямой. Кроме того, если функция
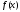 продолжена таким
продолжена таким
образом,
то (поскольку
 также
является периодической функцией периода
также
является периодической функцией периода
 )
длячетной
функции
)
длячетной
функции
 неравенство
(8.27)справедливо
всюду на прямой
неравенство
(8.27)справедливо
всюду на прямой
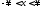 .
.
2)
Пусть теперь
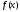 - произвольная функция, удовлетворяющая
условиям доказанной теоремы. Эту функцию
мы периодически с периодом
- произвольная функция, удовлетворяющая
условиям доказанной теоремы. Эту функцию
мы периодически с периодом продолжим
на всю прямую и составим с помощью этой
функции следующие четные функции:
продолжим
на всю прямую и составим с помощью этой
функции следующие четные функции:
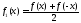 ;
(8.28)
;
(8.28)
 .
(8.29)
.
(8.29)
По
доказанному в 1) для любого
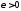 найдутся
тригонометрические многочлены
найдутся
тригонометрические многочлены
 и
и такие,
что всюду на числовой прямой
такие,
что всюду на числовой прямой
 ,
,
и поэтому
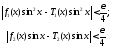 .
.
Складывая эти неравенства и учитывая, что модуль суммы двух величин не превосходит сумму их модулей, а также принимая во внимание равенства (8.28) и (8.29), получим, что всюду на числовой прямой справедливо неравенство
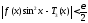 ,
(8.30)
,
(8.30)
в
котором через
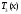 обозначен
тригонометрический многочлен, равный
обозначен
тригонометрический многочлен, равный .
.
В
проведенных нами рассуждениях вместо
функции
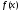 можно
взять функцию
можно
взять функцию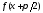 6.
В полной аналогии с (8.31) получим, что
для функции
6.
В полной аналогии с (8.31) получим, что
для функции найдется
тригонометрический многочлен
найдется
тригонометрический многочлен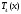 такой, что всюду на числовой прямой
такой, что всюду на числовой прямой
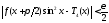 .
(8.31)
.
(8.31)
Заменяя
в (8.32)
 на
на и
обозначая через
и
обозначая через
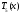 тригонометрический
многочлен вида
тригонометрический
многочлен вида
 ,
получим, что всюду на числовой прямой
справедливо неравенство
,
получим, что всюду на числовой прямой
справедливо неравенство
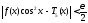 .
(8.32)
.
(8.32)
Наконец,
складывая неравенства (8.30) и (8.32) и
обозначая через
 тригонометрический
многочлен вида
тригонометрический
многочлен вида ,
получим, что всюду на числовой прямой
справедливо неравенство (8.26). Теорема
доказана.
,
получим, что всюду на числовой прямой
справедливо неравенство (8.26). Теорема
доказана.
Замечание.
Каждое из условий 1) непрерывности
 на
сегменте
на
сегменте
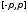 и 2) равенства значений
и 2) равенства значений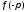 и
и
 являетсянеобходимым
условием для равномерного на сегменте
являетсянеобходимым
условием для равномерного на сегменте
 приближения функции
приближения функции тригонометрическими многочленами.
тригонометрическими многочленами.
Иными словами, теорему Вейерштрасса можно переформулировать следующим образом:
Теорема
8.7*.
Для того, чтобы функцию
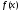 можно
было равномерно на сегменте
можно
было равномерно на сегменте
 приблизить
тригонометрическими многочленами,
необходимо и достаточно, чтобы функция
приблизить
тригонометрическими многочленами,
необходимо и достаточно, чтобы функция была непрерывной на сегменте
была непрерывной на сегменте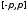 и удовлетворяла условию
и удовлетворяла условию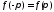 .
.
Достаточность составляет содержание теоремы 8.7.
Остановимся
на доказательстве необходимости.
Пусть существует последовательность
тригонометрических многочленов
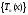 ,
равномерно на сегменте
,
равномерно на сегменте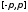 сходящихся
к функции
сходящихся
к функции
 .
Так как каждая функция
.
Так как каждая функция непрерывна
на сегменте
непрерывна
на сегменте ,
то по следствию 2 из теоремы 2.7 функция
,
то по следствию 2 из теоремы 2.7 функция непрерывна
на сегменте
непрерывна
на сегменте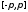 .
Для любого
.
Для любого найдется
многочлен
найдется
многочлен
 такой,
что
такой,
что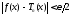 для
всех
для
всех из сегмента
из сегмента .
Следовательно,
.
Следовательно,
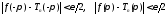 .
.
Из
последних двух неравенств и из вытекающего
из условия периодичности (с периодом
 )
равенства
)
равенства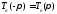 заключаем, что
заключаем, что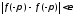 ,
откуда
,
откуда (в силу произвольности
(в силу произвольности ).
).
2. Доказательство замкнутости тригонометрической системы. Опираясь на теорему Вейерштрасса, докажем следующую основную теорему.
Теорема
8.8. Тригонометрическая система (8.10)
является замкнутой7,
т.е.
для любой кусочно непрерывной на сегменте
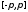 функции
функции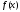 и
любого положительного числа
и
любого положительного числа найдется
тригонометрический многочлен
найдется
тригонометрический многочлен
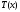 такой, что
такой, что
 .
(8.33)
.
(8.33)
Доказательство.
Прежде всего заметим, что для любой
кусочно непрерывной на сегменте
 функции
и для любого найдется непрерывная на
этом сегменте функция
функции
и для любого найдется непрерывная на
этом сегменте функция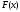 ,
удовлетворяющая условию
,
удовлетворяющая условию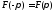 и такая, что
и такая, что
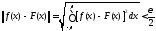 .
(8.34)
.
(8.34)
В
самом деле, достаточно взять функцию совпадающей с
совпадающей с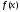 всюду, кроме достаточно малых
окрестностей точек разрыва функции
всюду, кроме достаточно малых
окрестностей точек разрыва функции и
точки
и
точки
 ,
а в
,
а в
указанных
окрестностях взять
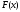 линейной
функцией так, чтобы
линейной
функцией так, чтобы являлась
непрерывной на всем сегменте
являлась
непрерывной на всем сегменте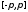 и
удовлетворяла условию
и
удовлетворяла условию
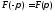 .
.
Так
как кусочно непрерывная функция и
срезающая ее линейная функция являются
ограниченными, то, выбирая указанные
окрестности точек разрыва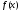 и точки
и точки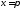 достаточно
малыми, мы обеспечим выполнение
неравенства (8.34).
достаточно
малыми, мы обеспечим выполнение
неравенства (8.34).
По
теореме Вейерштрасса 8.7 для функции
 найдется
тригонометрический многочлен
найдется
тригонометрический многочлен такой,
что для всех
такой,
что для всех из
сегмента
из
сегмента
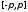 справедливо
неравенство
справедливо
неравенство
 .
(8.35)
.
(8.35)
Из (8.35) заключаем, что
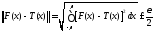 .
(8.36)
.
(8.36)
Из (8.34) и (8.36) и из неравенства треугольника для норм вытекает неравенство (8.33). Теорема доказано.
Замечание.
Из теорем 8.8 и 8.5 сразу же вытекает, что
тригонометрическая
система
(8.10) является
полной.
Отсюда в свою очередь вытекает, что
система
 является
полной на множестве всех функций, кусочно
непрерывных на сегменте
является
полной на множестве всех функций, кусочно
непрерывных на сегменте
 (или соответственно на сегменте
(или соответственно на сегменте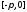 ).В
самом деле, всякая кусочно непрерывная
на сегменте
).В
самом деле, всякая кусочно непрерывная
на сегменте
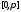 функция
функция ,
ортогональная на этом сегменте всем
элементам системы
,
ортогональная на этом сегменте всем
элементам системы ,
после нечетного продолжения на сегмент
,
после нечетного продолжения на сегмент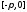 оказывается
ортогональной на сегменте
оказывается
ортогональной на сегменте
 всем
элементам тригонометрической системы
(8.10). В силу полноты системы (8.10) эта
функция равна нулю на
всем
элементам тригонометрической системы
(8.10). В силу полноты системы (8.10) эта
функция равна нулю на
 ,
а следовательно, на
,
а следовательно, на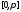 .
Совершенно аналогично доказывается,
что система
.
Совершенно аналогично доказывается,
что система ,
,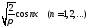 является полной на множестве всех
функций, кусочно непрерывных на сегменте
является полной на множестве всех
функций, кусочно непрерывных на сегменте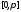 (или соответственно на сегменте
(или соответственно на сегменте ).
).
