3. Следствия замкнутости тригонометрической системы.

Следствие 1. Для любой кусочно непрерывной на сегменте функциисправедливо равенство Парсеваля

(8.37)

(вытекает из теоремы 8.3).

Следствие 2. Тригонометрический ряд Фурье любой кусочно непрерывной на сегментефункциисходится к этой функции на указанном сегменте в среднем (вытекает из теоремы 8.4 и замечания к ней).

Следствие 3. Тригонометрический ряд Фурье любой кусочно непрерывной на сегментефункции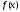можно почленно интегрировать на этом сегменте(вытекает из предыдущего следствия и из теоремы 2.11).

Следствие 4. Если две кусочно непрерывные на сегменте функциии имеют одинаковые тригонометрические ряды Фурье, то эти функции совпадают всюду на этом сегменте (вытекает из теоремы 8.6).

Следствие 5. Если тригонометрический ряд Фурье кусочно непрерывной на сегменте 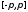функциисходится равномерно на некотором содержащемся в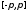 сегменте , то он сходится на сегментеименно к функции.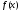

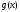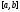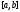Доказательство. Пусть - та функция, к которой сходится равномерно на тригонометрический ряд Фурье функции . Докажем, чтовсюду на сегменте . Так как из равномерной сходимости на сегменте вытекает сходимость в среднем на этом сегменте (см. п.3 § 4. гл.2), то тригонометрический ряд Фурье функции сходится к функции на сегментев среднем. Это означает, что для произвольного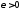найдется номер, начиная с которогоn-я частичная сумма тригонометрического ряда Фурье удовлетворяет неравенству

. (8.38)

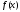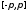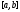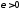С другой стороны, в силу следствия 2 последовательность сходится к в среднем на всем сегменте , а следовательно, и на сегменте, т.е. для фиксированного нами произвольногонайдется номер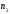, начиная с которого

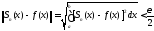. (8.39)

Из (8.38) и (8.39) и из неравенства треугольника

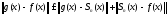
вытекает, что 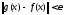. Из этого неравенства и из произвольностиследует, что 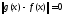, а отсюда на основании первого свойства нормы заключаем, что- нулевой элемент пространства кусочно непрерывных на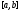 функций, т.е. функция тождественно равная нулю на сегменте 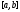. Следствие 5 доказано.

Замечание. Конечно, в следствии 5 сегмент 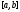может совпадать со всем сегментом, т.е. из равномерной сходимости ряда Фурье функции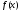на всем сегменте 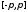следует, что этот ряд сходится на указанном сегменте именно к функции .

§4. Простейшие условия равномерной сходимости и почленного дифференцирования тригонометрического ряда фурье

1. Вводные замечания. В математической физике и в ряде других разделов математики существенную роль играет вопрос об условиях, при выполнении которых тригонометрический ряд Фурье функции 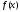сходится (к этой функции) в данной точкесегмента .

Еще в конце прошлого века было известно, что существуют непрерывные на сегменте функции, удовлетворяющие условию, тригонометрические ряды Фурье которых расходятся в наперед заданной точке сегмента(или даже расходятся на бесконечном множестве точек сегмента, всюду плотном на этом сегменте)⁸.

Таким образом, одна непрерывность функции на сегментебез дополнительных условий не обеспечивает не только равномерную сходимость тригонометрического ряда Фурье этой функции, но даже сходимость этого ряда в наперед заданной точке указанного сегмента.

В этом и следующем параграфах мы выясним, какие требования следует добавить к непрерывности функции(или ввести взамен непрерывности) для обеспечения сходимости тригонометрического ряда Фурье этой функции в заданной точке, а также для обеспечения равномерной сходимости этого ряда на всем сегменте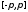 или на какой-либо его части.

При изучении сходимости тригонометрического ряда Фурье возникает и другой вопрос: должен ли тригонометрический ряд Фурье любой кусочно непрерывной (или даже строго непрерывной) на сегменте 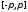функции 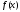сходится хотя бы в одной точке этого сегмента?

Положительный ответ на этот вопрос был получен только в 1966г.