
- •Глава 8 ряды фурье
- •§1. Ортонормированные системы и общие ряды фурье
- •§2. Замкнутые и полные ортонормированные системы
- •§3. Замкнутость тригонометрической системы и следствия из нее
- •3. Следствия замкнутости тригонометрической системы.
- •§4. Простейшие условия равномерной сходимости и почленного дифференцирования тригонометрического ряда фурье
- •2. Простейшие условия абсолютной и равномерной сходимости тригонометрического ряда Фурье.
- •§5. Более точные условия равномерной сходимости и условия сходимости в данной точке
- •3. Вспомогательные предложения.
§5. Более точные условия равномерной сходимости и условия сходимости в данной точке
1. Модуль непрерывности функции. Классы Гёльдера. Введем понятия, характеризующие гладкость изучаемых функций, и определим классы функций, в терминах которых будут сформулированы условия сходимости тригонометрического ряда Фурье.
Пусть
функция
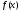 определена
и непрерывна на сегменте
определена
и непрерывна на сегменте
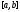 .
.
Определение
1. Для каждого
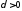 назовем модулем непрерывности функции
назовем модулем непрерывности функции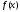 на
сегменте
на
сегменте
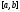 точную
верхнюю грань модуля
точную
верхнюю грань модуля
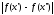 на
на
множестве
всех
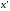 и
и
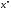 ,принадлежащих
сегменту
,принадлежащих
сегменту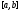 и
удовлетворяющих условию
и
удовлетворяющих условию
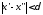 .
.
Будем
обозначать модуль непрерывности функции
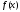 на
сегменте
на
сегменте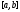 символом
символом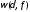 .
Итак,
по
определению
.
Итак,
по
определению
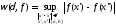 .
.
Непосредственно
из теоремы Кантора (см. теорему 4.16 ч. 1)
вытекает, что модуль
непрерывности
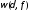 любой
непрерывной на сегменте
любой
непрерывной на сегменте
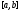 функции
функции
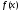 стремится
к нулю при
стремится
к нулю при
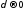 14.
Однако для произвольной только
непрерывной на сегменте
14.
Однако для произвольной только
непрерывной на сегменте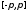 функции
функции
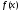 нельзя,
вообще говоря, ничего сказать о порядке
ее модуля непрерывности
нельзя,
вообще говоря, ничего сказать о порядке
ее модуля непрерывности
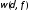 относительно
малого
относительно
малого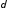 .
Рассмотрим дифференцируемые на сегменте
функции.
.
Рассмотрим дифференцируемые на сегменте
функции.
Утверждение.
Если функция
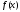 дифференцируема
на сегменте
дифференцируема
на сегменте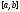 и
ее производная
и
ее производная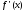 ограничена на этом сегменте, то модуль
непрерывности функции
ограничена на этом сегменте, то модуль
непрерывности функции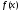 на
указанном сегменте
на
указанном сегменте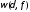 имеет
порядок
имеет
порядок
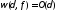 15.
В самом деле, из теоремы Лагранжа16вытекает, что для любых точек
15.
В самом деле, из теоремы Лагранжа16вытекает, что для любых точек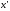 и
и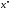 сегмента
сегмента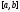 найдется точка
найдется точка
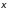 ,
заключенная между
,
заключенная между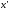 и
и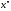 и такая, что
и такая, что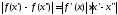 .
(8.48)
.
(8.48)
Так
как производная
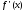 ограниченна
на сегменте
ограниченна
на сегменте
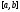 ,
то найдется постоянная
,
то найдется постоянная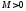 такая,
что для всех
такая,
что для всех из
этого сегмента
из
этого сегмента
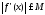 и,
следовательно,
и,
следовательно,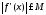 .Из
последнего неравенства и из (8.48) заключаем,
что
.Из
последнего неравенства и из (8.48) заключаем,
что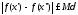 для
всех
для
всех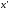 и
и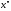 из
из
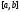 ,
удовлетворяющих условию
,
удовлетворяющих условию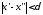 .
Но это и означает, что
.
Но это и означает, что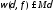 ,
т.е.
,
т.е.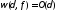 .
.
Пусть
 - любое вещественное число из полусегмента
- любое вещественное число из полусегмента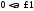 .
.
Определение
2. Будем говорить, что функция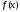 принадлежит на сегменте
принадлежит на сегменте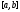 классу Гёльдера
классу Гёльдера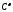 с
показателем
с
показателем
 (
(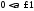 ),
если модуль непрерывности
),
если модуль непрерывности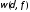 функции
функции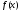 на
сегменте
на
сегменте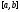 имеет
порядок
имеет
порядок
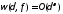 .
.
Для
обозначения того, что функция
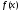 принадлежит
на сегменте
принадлежит
на сегменте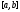 классу
Гёльдера
классу
Гёльдера
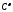 ,
обычно употребляют символику
,
обычно употребляют символику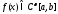 .
.
Сразу
же отметим, что если на сегменте
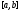 функция
функция
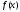 дифференцируема
и ее производная ограничена, то эта
функция заведомо принадлежит на этом
сегменте классу Гёльдера
дифференцируема
и ее производная ограничена, то эта
функция заведомо принадлежит на этом
сегменте классу Гёльдера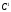 (это
утверждение непосредственно вытекает
из
(это
утверждение непосредственно вытекает
из
доказанного
выше соотношения
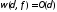 )17.Замечание.
Пусть
)17.Замечание.
Пусть
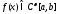 .Точную
верхнюю грань дроби
.Точную
верхнюю грань дроби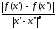 на
множестве всех
на
множестве всех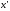 и
и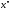 ,принадлежащих
сегменту
,принадлежащих
сегменту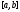 и
не равных друг другу, называют константой
Гёльдера
(или коэффициентом
Гёльдера)
функции
и
не равных друг другу, называют константой
Гёльдера
(или коэффициентом
Гёльдера)
функции
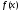 (на сегменте
(на сегменте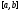 ).
Сумму константы Гёльдера функции
).
Сумму константы Гёльдера функции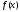 на
сегменте
на
сегменте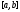 и
точной верхней грани
и
точной верхней грани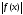 на
этом сегменте называютгёльдеровой
нормой функции
на
этом сегменте называютгёльдеровой
нормой функции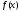 на
сегменте
на
сегменте
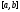 и
обозначают символом
и
обозначают символом
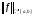 .
.
Пример.
Функция
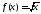 принадлежит
на сегменте
принадлежит
на сегменте
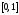 классу
классу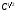 ,
так как для любых
,
так как для любых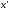 и
и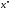 из
из
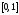 ,
связанных условием
,
связанных условием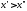 ,
справедливо равенство
,
справедливо равенство
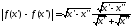
(при
этом константа Гёльдера, являющаяся
точной верхней гранью на
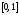 дроби
дроби
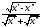 ,
равна единице, а гёльдерова норма равна
двум).
,
равна единице, а гёльдерова норма равна
двум).
2.
Выражение для частичной суммы
тригонометрического ряда Фурье.
Пусть
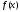 -
произвольная функция, определенная и
кусочно непрерывная на сегменте
-
произвольная функция, определенная и
кусочно непрерывная на сегменте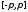 .
.
Мы
будем называть периодическим
продолжением
этой функции на всю прямую такую
определенную на всей прямой функцию
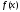 18,которая
удовлетворяет трем требованиям: 1)
совпадает с первоначально заданной
функцией на интервале
18,которая
удовлетворяет трем требованиям: 1)
совпадает с первоначально заданной
функцией на интервале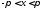 ,
,
2)
имеет на концах сегмента
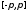 значения
значения
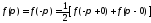 ,
,
3)
удовлетворяет условию периодичности
с периодом
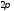 ,
т.е. удовлетворяет для любого
,
т.е. удовлетворяет для любого соотношению
соотношению
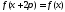 .
.
Лемма.
Если функция
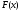 является
периодическим продолжением на всю
числовую прямую функции
является
периодическим продолжением на всю
числовую прямую функции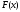 ,
первоначально определенной и кусочно
непрерывной на сегменте
,
первоначально определенной и кусочно
непрерывной на сегменте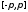 ,
то все интегралы этой функции по любому
отрезку длины
,
то все интегралы этой функции по любому
отрезку длины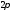 равны
друг другу, т.е. для любого
равны
друг другу, т.е. для любого
 справедливо равенство
справедливо равенство
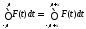 .
(8.49)
.
(8.49)
Доказательство. В силу свойства аддитивности интеграла имеем
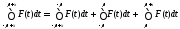 .
(8.50)
.
(8.50)
Используя
условие периодичности
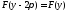 ,
с помощью замены
,
с помощью замены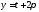 получим
получим
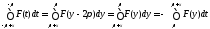 .
(8.51)
.
(8.51)
Из (8.50) и (8.51) вытекает соотношение (8.49). Лемма доказана.
Пусть
теперь функция
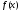 является
периодическим продолжением на всю
прямую функции
является
периодическим продолжением на всю
прямую функции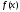 ,
первоначально определенной и кусочно
непрерывной на сегменте
,
первоначально определенной и кусочно
непрерывной на сегменте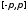 .
.
Вычислим
для этой функции в любой точке
 частичную сумму ее тригонометрического
ряда Фурье
частичную сумму ее тригонометрического
ряда Фурье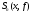 ,
имеющую вид
,
имеющую вид
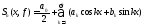 .
.
Используя выражение для коэффициентов Фурье
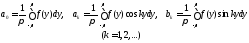
и
свойство линейности интеграла, выражение
для
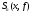 можно
переписать в следующем виде:
можно
переписать в следующем виде:
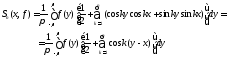 .
.
Сделаем
в последнем интеграле замену переменной
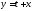 :
:
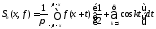 .
.
Наконец,
используя лемму 1 и замечая, что
подынтегральная функция в последнем
интеграле является периодической
функцией аргумента
 с
периодом
с
периодом
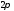 ,
получим
,
получим
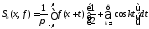 .
(8.52)
.
(8.52)
Вычислим
сумму, стоящую в (8.52) в квадратных скобках.
Для этого заметим, что для любого номера
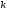 и
любого значения
и
любого значения справедливо
равенство
справедливо
равенство
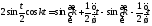 .
.
Просуммируем
это равенство по всем номерам
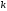 ,
равным
,
равным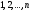 :
:
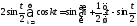 .
.
Отсюда
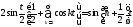
и, следовательно,
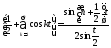 .
(8.53)
.
(8.53)
Подставляя (8.53) в (8.52),окончательно получим следующее выражение для n - й частичной суммы тригонометрического ряда Фурье:
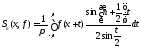 ,
(8.54)
,
(8.54)
справедливое
в любой точке
 числовой
прямой.
числовой
прямой.
Замечание.
Из формулы (8.54) и из того, что все частичные
суммы
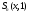 функции
функции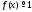 равны единице19,
вытекает следующее равенство:
равны единице19,
вытекает следующее равенство: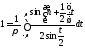 .
(8.55)
.
(8.55)
