
- •Глава 8 ряды фурье
- •§1. Ортонормированные системы и общие ряды фурье
- •§2. Замкнутые и полные ортонормированные системы
- •§3. Замкнутость тригонометрической системы и следствия из нее
- •3. Следствия замкнутости тригонометрической системы.
- •§4. Простейшие условия равномерной сходимости и почленного дифференцирования тригонометрического ряда фурье
- •2. Простейшие условия абсолютной и равномерной сходимости тригонометрического ряда Фурье.
- •§5. Более точные условия равномерной сходимости и условия сходимости в данной точке
- •3. Вспомогательные предложения.
2. Простейшие условия абсолютной и равномерной сходимости тригонометрического ряда Фурье.
Определение
1. Будем говорить, что функция
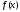 имеет на сегменте
имеет на сегменте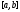 кусочно непрерывную производную, если
производная
кусочно непрерывную производную, если
производная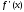 существует и непрерывна всюду на
сегменте
существует и непрерывна всюду на
сегменте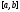 ,
за исключением, быть может, конечного
числа точек, в каждой из которых функция
,
за исключением, быть может, конечного
числа точек, в каждой из которых функция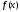 имеет конечные правое и левое предельные
значения9.
имеет конечные правое и левое предельные
значения9.
Определение
2. Будем говорить, что функция
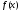 имеет на сегменте
имеет на сегменте кусочно
непрерывную производную порядка n
кусочно
непрерывную производную порядка n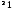 ,
если функция
,
если функция
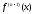 имеет на этом сегменте кусочно непрерывную
производную в смысле определения 1.
имеет на этом сегменте кусочно непрерывную
производную в смысле определения 1.
Теорема
8.9. Если функция
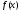 непрерывна
на сегменте
непрерывна
на сегменте
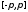 ,
имеет на этом сегменте кусочно непрерывную
производную и удовлетворяет условию
,
имеет на этом сегменте кусочно непрерывную
производную и удовлетворяет условию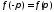 ,
то тригонометрический ряд Фурье
функции
,
то тригонометрический ряд Фурье
функции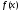 сходится к этой функции
сходится к этой функции
равномерно
на сегменте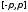 .
Более того, ряд составленный из модулей
членов тригонометрического ряда Фурье
функции
.
Более того, ряд составленный из модулей
членов тригонометрического ряда Фурье
функции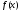 ,сходится
равномерно на сегменте
,сходится
равномерно на сегменте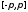 .
.
Доказательство.
Достаточно доказать, что ряд, составленный
из модулей членов тригонометрического
ряда Фурье функции
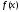 :
:
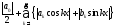 ,
(8.40)
,
(8.40)
сходится
равномерно на сегменте
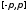 ,
так как отсюда будет вытекать как
равномерная на сегменте
,
так как отсюда будет вытекать как
равномерная на сегменте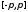 сходимость самого тригонометрического
ряда Фурье функции
сходимость самого тригонометрического
ряда Фурье функции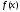 ,
так и сходимость этого ряда (в силу
следствия 5 из п. 3 § 3) именно к функции
,
так и сходимость этого ряда (в силу
следствия 5 из п. 3 § 3) именно к функции .
.
В
силу признака Вейерштрасса (см. теорему
2.3) для доказательства равномерной на
сегменте
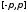 сходимости
ряда (8.40) достаточно доказать сходимость
мажорирующего его числового ряда
сходимости
ряда (8.40) достаточно доказать сходимость
мажорирующего его числового ряда
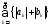 .
(8.41)
.
(8.41)
Обозначим
через
 и
и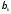 тригонометрические
коэффициенты Фурье функции
тригонометрические
коэффициенты Фурье функции
 ,
доопределив эту функцию произвольным
образом в конечном числе точек, в которых
не существует производная функции
,
доопределив эту функцию произвольным
образом в конечном числе точек, в которых
не существует производная функции 10.
10.
Производя
интегрирование по частям и учитывая,
что функция
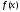 непрерывна на всем сегменте
непрерывна на всем сегменте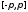 и
удовлетворяет соотношениям
и
удовлетворяет соотношениям
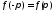 ,
получим следующие соотношения:
,
получим следующие соотношения:
 ,
,
которые
связывают между собой тригонометрические
коэффициенты Фурье функции
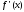 и
самой функции
и
самой функции
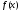 11.
Таким образом,
11.
Таким образом,
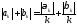 ,
,
и для доказательства сходимости ряда (8.41) достаточно доказать сходимость ряда
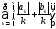 .
(8.42)
.
(8.42)
Сходимость
ряда (8.42) вытекает из элементарных
неравенств12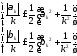 ;
(8.43)
;
(8.43)
и из сходимости рядов
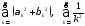 ,
(8.44)
,
(8.44)
первый
из которых сходится в силу равенства
Парсеваля для кусочно непрерывной
функции
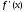 ,
а второй – в силу интегрального признака
Коши-Маклорена (см. п. 4 § 2 гл. 1). Теорема
доказана.
,
а второй – в силу интегрального признака
Коши-Маклорена (см. п. 4 § 2 гл. 1). Теорема
доказана.
Замечание.
Если функцию
 ,
удовлетворяющую условиям теоремы 8.9,
периодически (с периодом
,
удовлетворяющую условиям теоремы 8.9,
периодически (с периодом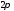 )
продолжить на всю бесконечную прямую,
то теорема 8.9 будет утверждать сходимость
тригонометрического ряда Фурье к так
продолженной функции,равномерную
на всей бесконечной прямой.
)
продолжить на всю бесконечную прямую,
то теорема 8.9 будет утверждать сходимость
тригонометрического ряда Фурье к так
продолженной функции,равномерную
на всей бесконечной прямой.
3. Простейшие условия почленного дифференцирования тригонометрического ряда Фурье. Прежде всего докажем следующую лемму о порядке тригонометрических коэффициентов Фурье.
Лемма.
Пусть функция
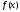 и
все ее производные до некоторого порядка
m
(m
– целое неотрицательное число) непрерывны
на сегменте
и
все ее производные до некоторого порядка
m
(m
– целое неотрицательное число) непрерывны
на сегменте
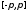 и удовлетворяют условиям
и удовлетворяют условиям
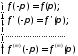 .
(8.45)
.
(8.45)
Пусть,
кроме того, функция
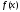 имеет
на сегменте
имеет
на сегменте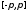 кусочно
непрерывную производную порядкаm+1.
Тогда сходится следующий ряд:
кусочно
непрерывную производную порядкаm+1.
Тогда сходится следующий ряд:
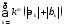 ,
(8.46)
,
(8.46)
в
котором
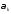 и
и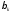 –
тригонометрические коэффициенты Фурье
функции
–
тригонометрические коэффициенты Фурье
функции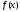 .
.
Доказательство.
Обозначим через
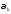 и
и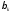 тригонометрические
коэффициенты Фурье функции
тригонометрические
коэффициенты Фурье функции
 ,
доопределив эту функцию произвольным
образом в конечном числе точек, в которых
не существует производной порядкаm+1
функции
,
доопределив эту функцию произвольным
образом в конечном числе точек, в которых
не существует производной порядкаm+1
функции
 .
Интегрируя выражения для
.
Интегрируя выражения для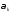 и
и
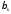 m+1-
раз по частям и учитывая непрерывность
на всем сегменте
m+1-
раз по частям и учитывая непрерывность
на всем сегменте
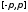 самой
функции
самой
функции
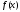 и
всех ее производных до порядка m,
а также используя соотношения (8.45),
установим следующую связь между
тригонометрическими коэффициентами
Фурье функции
и
всех ее производных до порядка m,
а также используя соотношения (8.45),
установим следующую связь между
тригонометрическими коэффициентами
Фурье функции
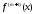 и
самой
и
самой
функции
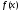 13:
13: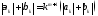 .
.
Таким образом,
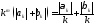 ,
,
и
сходимость ряда (8.46) вытекает из
элементарных неравенств (8.43) и из
сходимости рядов (8.44), первый из которых
сходится в силу равенства Парсеваля
для кусочно непрерывной функции
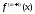 ,
а второй – в силу признака Коши-Маклорена.
Лемма доказана.
,
а второй – в силу признака Коши-Маклорена.
Лемма доказана.
Непосредственным следствием леммы 1 является следующая теорема.
Теорема
8.10. Пусть функция
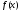 удовлетворяет
тем же условиям, что и в лемме 1, причем
m
удовлетворяет
тем же условиям, что и в лемме 1, причем
m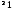 .
Тогда тригонометрический ряд Фурье
функции
.
Тогда тригонометрический ряд Фурье
функции
 можно
m
раз можно почленно дифференцировать
на сегменте
можно
m
раз можно почленно дифференцировать
на сегменте
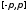 .
.
Доказательство.
Пусть s
- любое из чисел
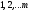 .
В результатеs
– кратного почленного дифференцирования
тригонометрического ряда Фурье функции
.
В результатеs
– кратного почленного дифференцирования
тригонометрического ряда Фурье функции
 получается
ряд
получается
ряд
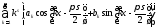 .
(8.47)
.
(8.47)
Заметим,
что для всех
 из
сегмента
из
сегмента
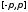 как
исходный тригонометрический ряд Фурье,
так и ряд (8.47) (с любым
как
исходный тригонометрический ряд Фурье,
так и ряд (8.47) (с любым
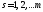 )
мажорируются сходящимся числовым рядом
(8.46). По признаку Вейерштрасса (см.
теорему 2.3) как исходный тригонометрический
ряд Фурье, так и каждый из рядов (8.47) (при
)
мажорируются сходящимся числовым рядом
(8.46). По признаку Вейерштрасса (см.
теорему 2.3) как исходный тригонометрический
ряд Фурье, так и каждый из рядов (8.47) (при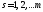 )
сходятся равномерно на сегменте
)
сходятся равномерно на сегменте ,
а это (в силу теоремы 2.9) обеспечивает
возможностьm
– кратного почленного дифференцирования
исходного ряда Фурье. Теорема доказана.
,
а это (в силу теоремы 2.9) обеспечивает
возможностьm
– кратного почленного дифференцирования
исходного ряда Фурье. Теорема доказана.
