§ 10. Формула Грина.

Выведем формулу Грина, связывающую криволинейный интеграл 2-го рода по замкнутой кривой с двойным интегралом по области, ограниченной этой кривой.

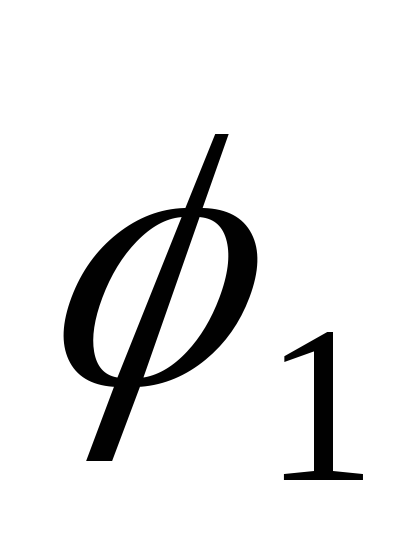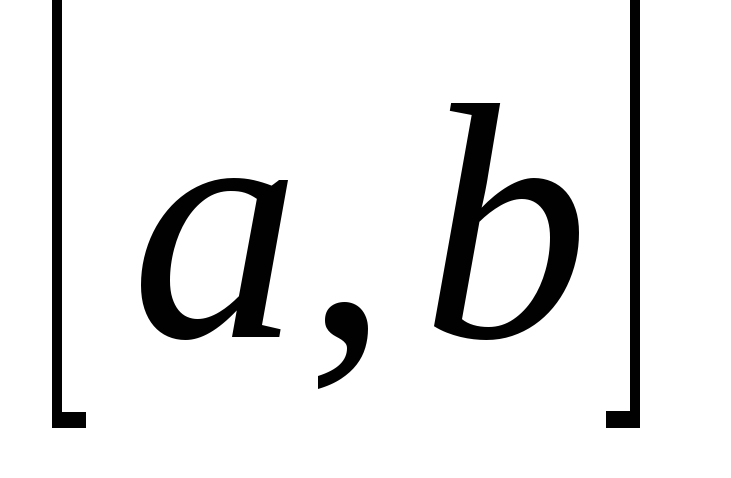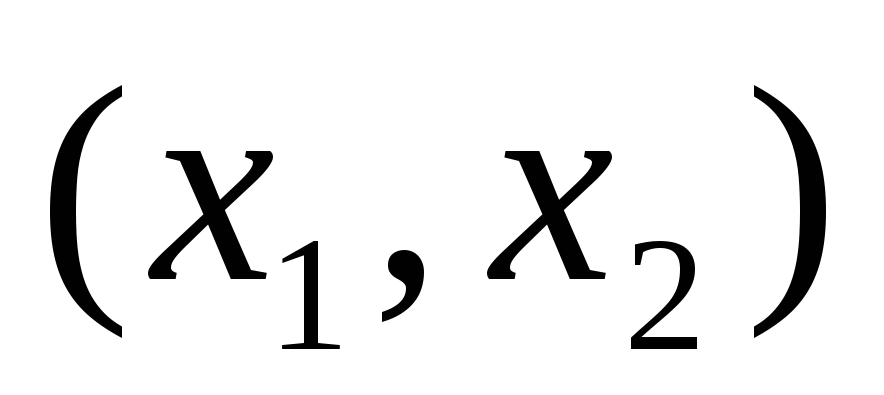Пусть и-непрерывные функции на отрезке. Множество точекплоскостиназывается криволинейной трапецией по отношению к первой оси координат, есл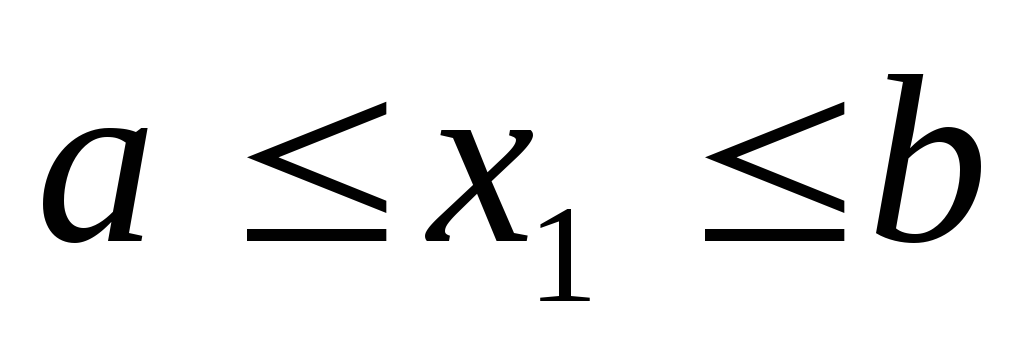ии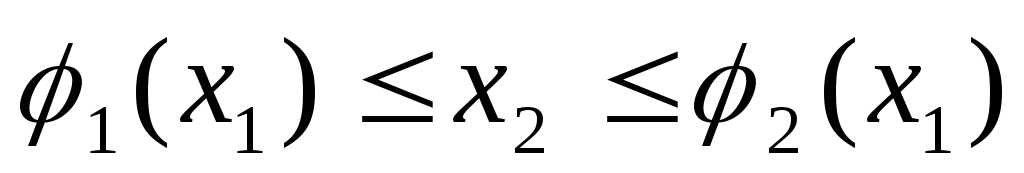(рис. 3.) Аналогично, меняя ролям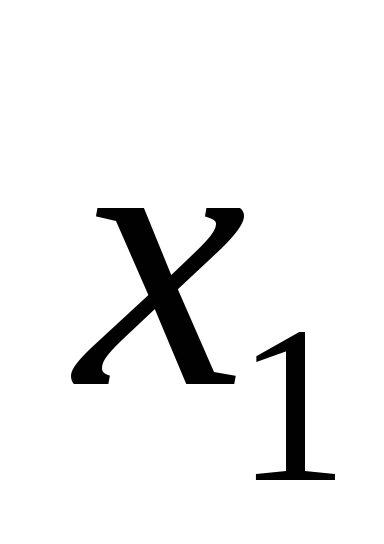ии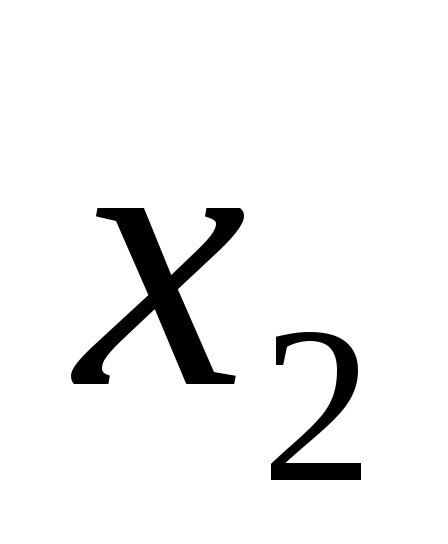, определяется криволинейная трапеция по отношению ко второй оси координат. Множествоточек плоскостиназывается элементарной областью, если его можно разбить на конечное число криволинейных трапеций по отношению к каждой оси системы координат. Черезбудем обозначать границу областис направлением, соответствующим направлению кратчайшего поворота от первой оси ко второй оси системы координат.

Теорема 1. Пусть область элементарна, а функции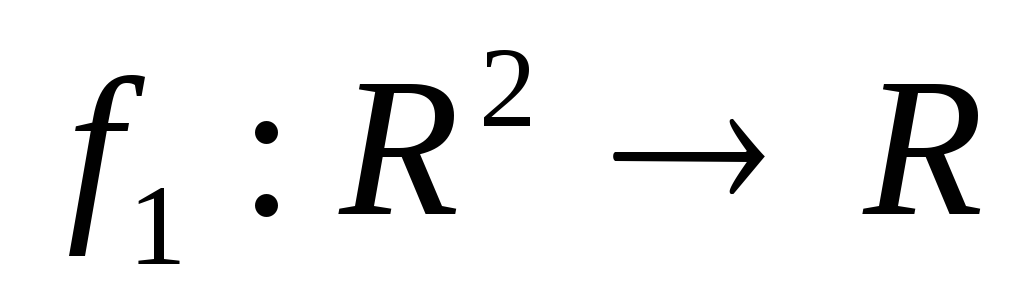,,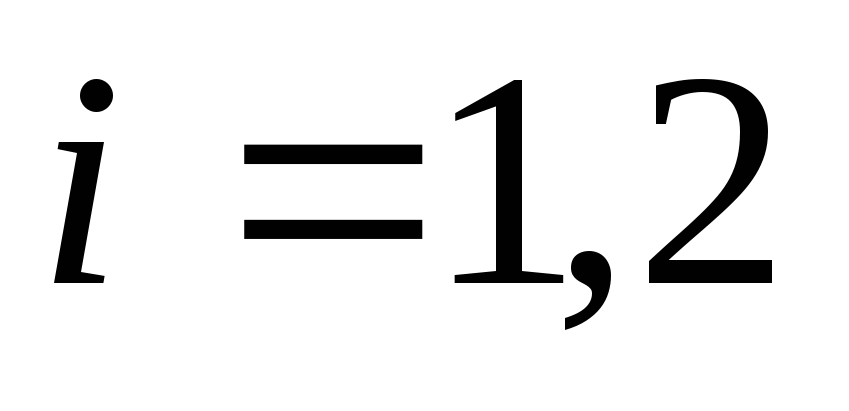 имеют непрерывную производную в некоторой открытой области, содержащей областьвместе с её границей. Тогда справедлива формула Грина

.

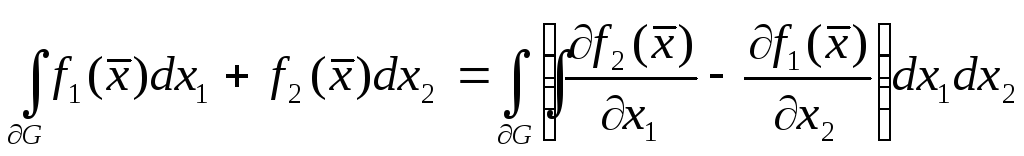Доказательство. Достаточно доказать формулы

,

.

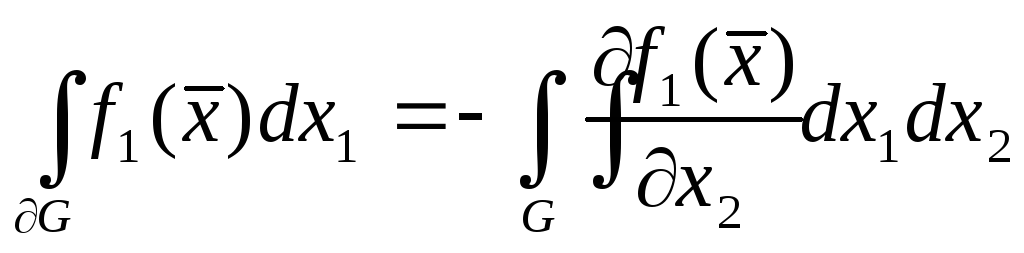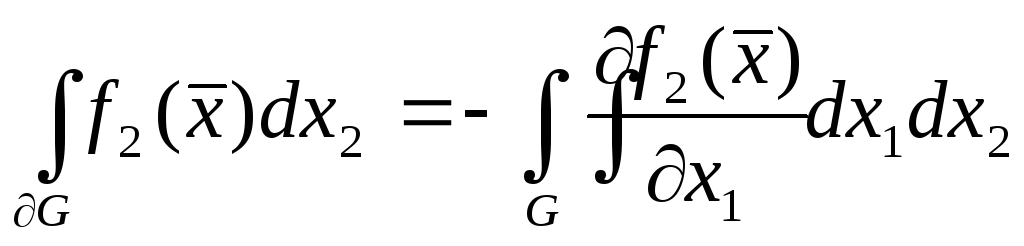Так как они доказываются одинаково, то ограничимся доказательством только первой из них. Более того, ввиду элементарности области достаточно доказать эту формулу только для одной криволинейной трапеции по отношению, например, к первой оси координат. Применяя теорему Фубини и формулу Ньютона-Лейбница, получим

.

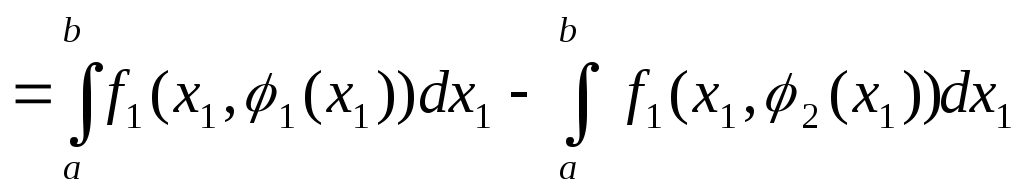Разобьем границу 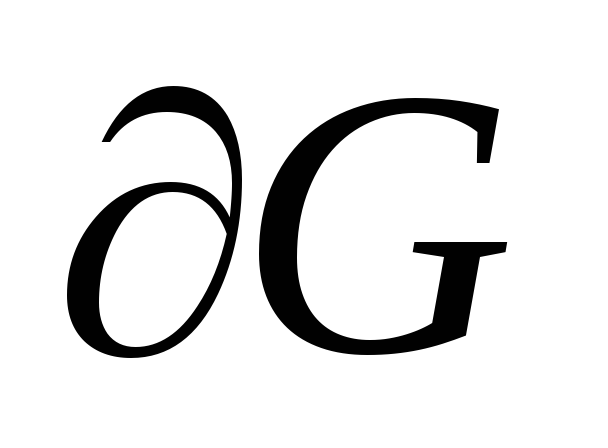областина 4 части: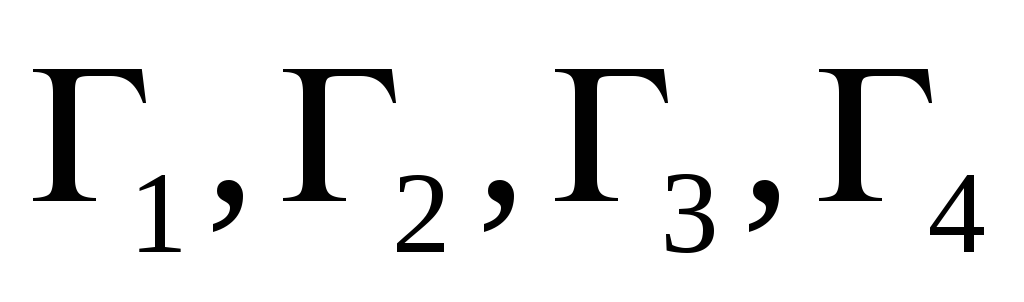

,

,

,

.

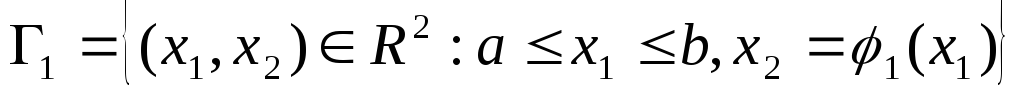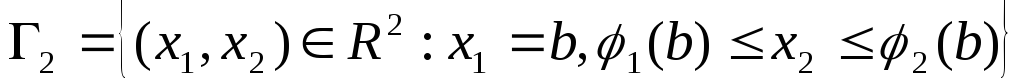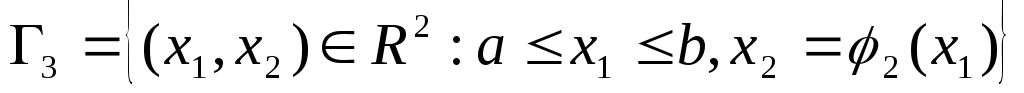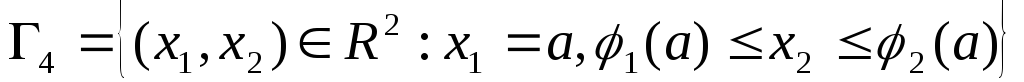Так как

,

.

=,

,

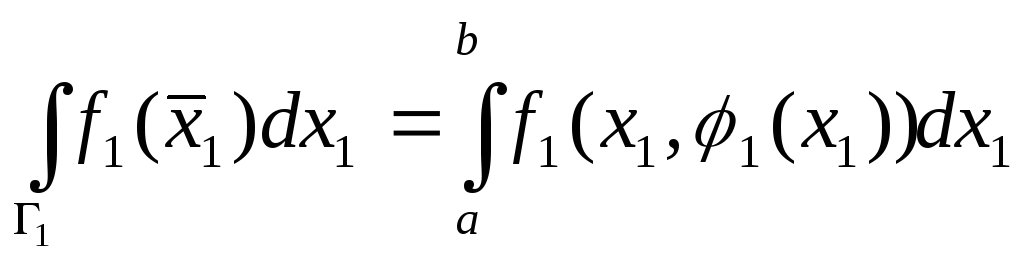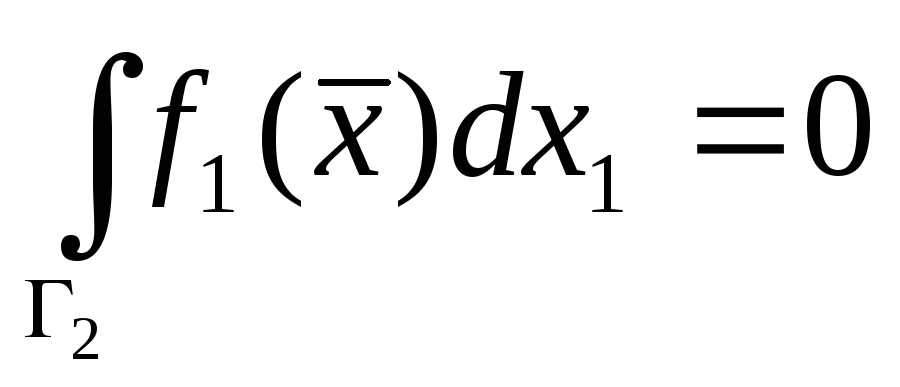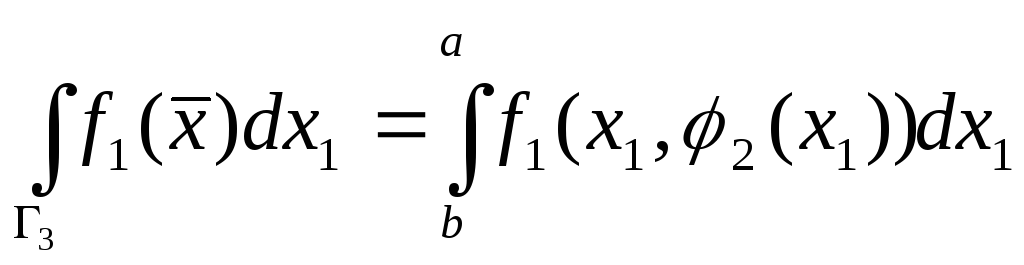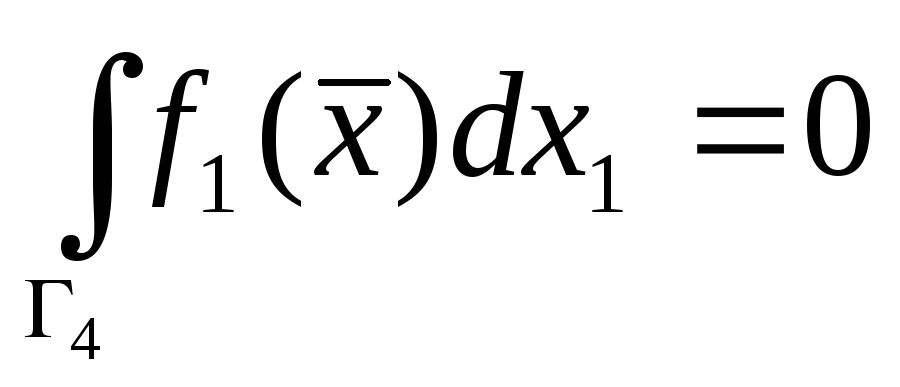то

.

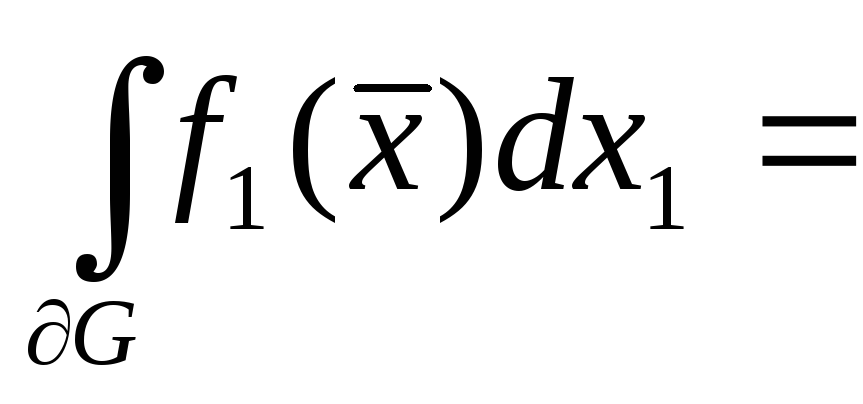
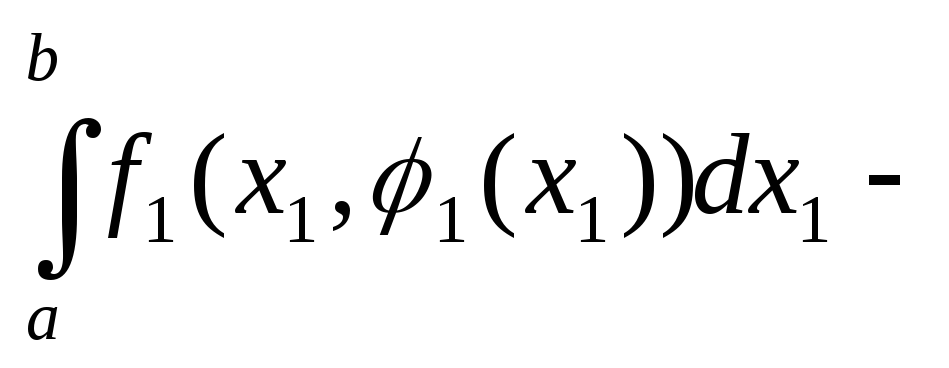
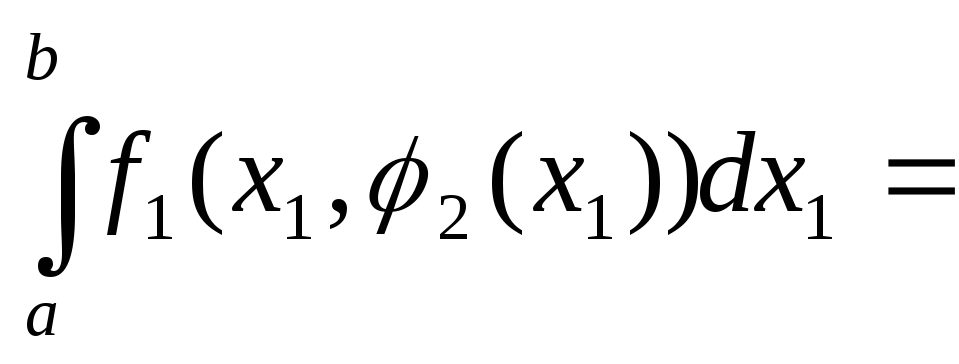
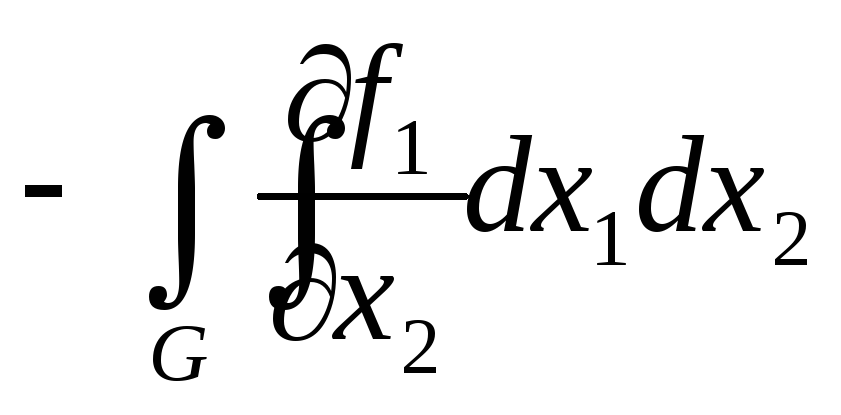Теорема доказана.

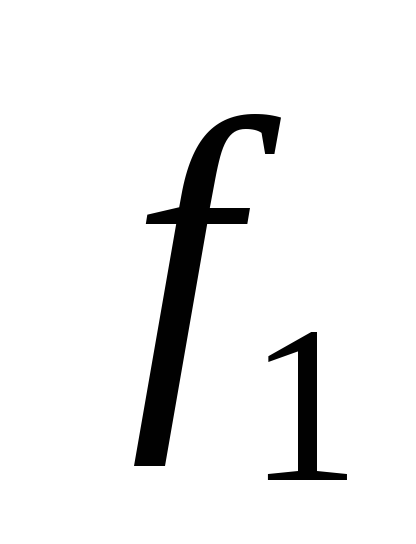Следствие 1. Если в элементарной области для непрерывно дифференцируемых функцийи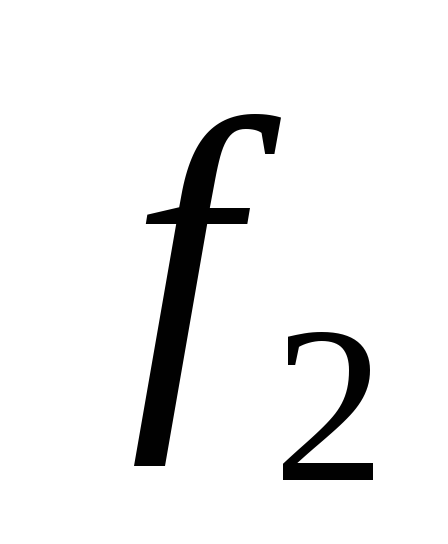выполняется равенство

,

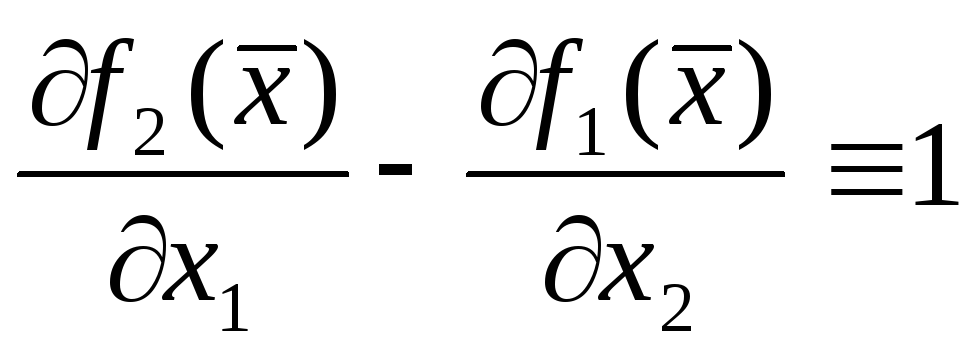то

.

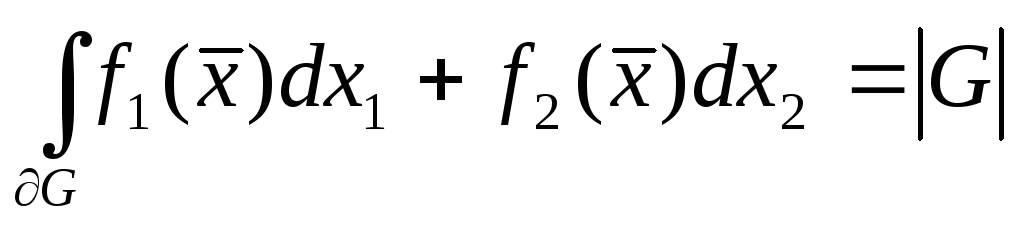В частности

, .

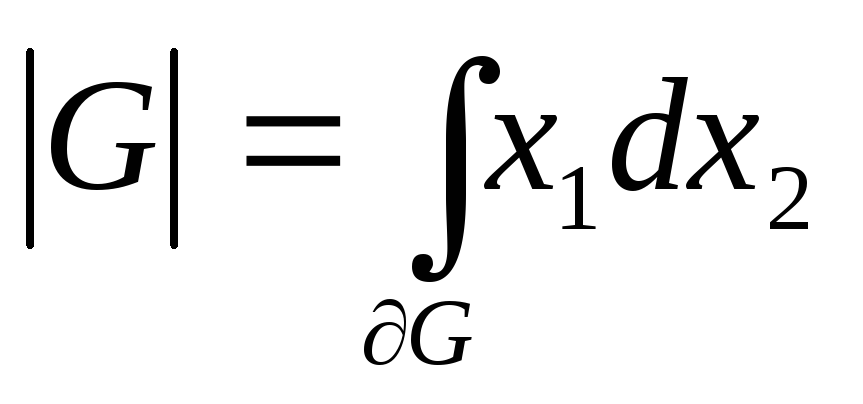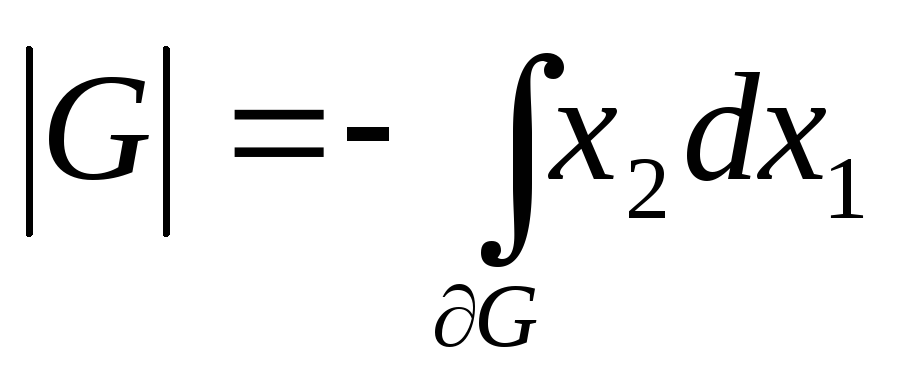Доказательство следует из формулы Грина с учетом того, что

.

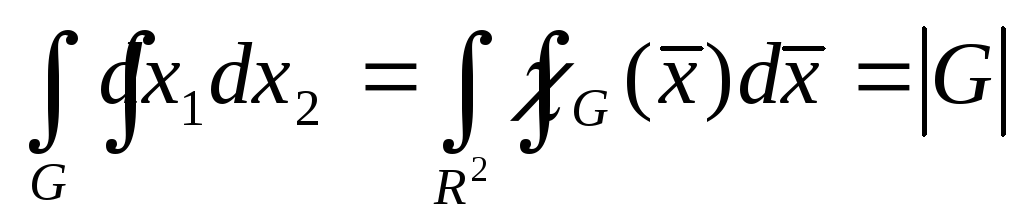Таким образом меру области , или площадь области, можно вычислять с помощью криволинейных интегралов 2-го рода по границе этой области.

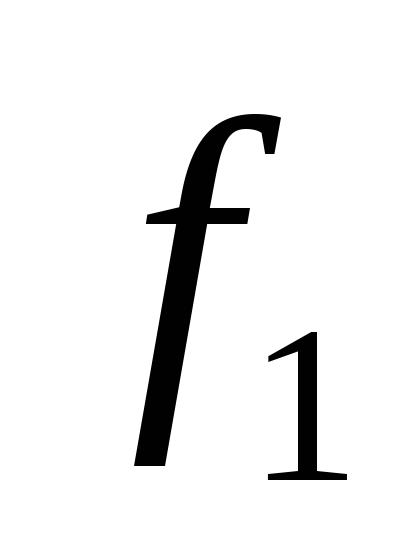Следствие 2. Если в элементарной области для непрерывно дифференцируемых функцийи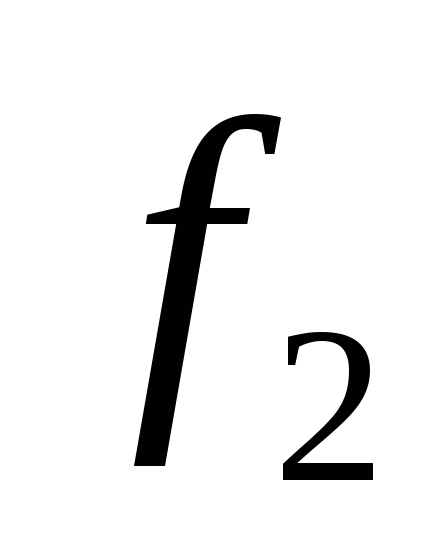выполняется равенство

,

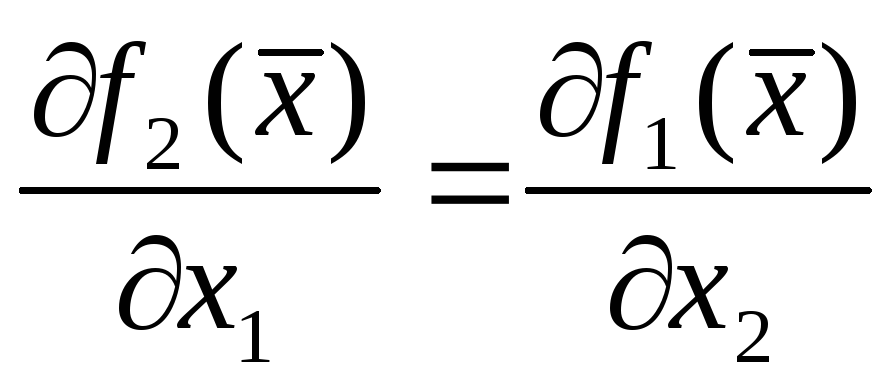то

.

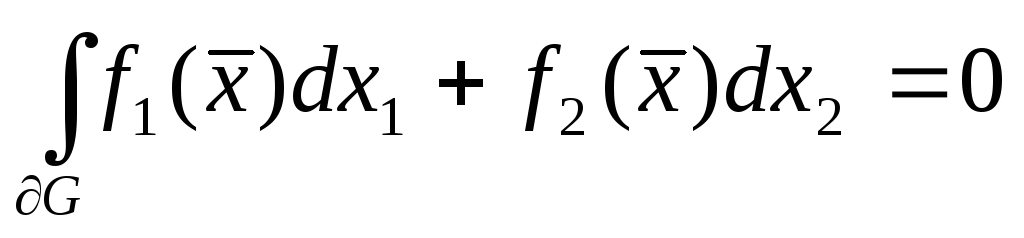Доказательство сразу следует из формулы Грина.
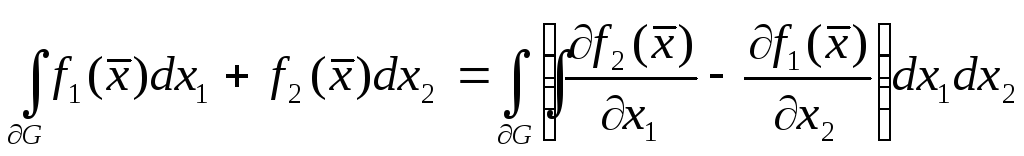
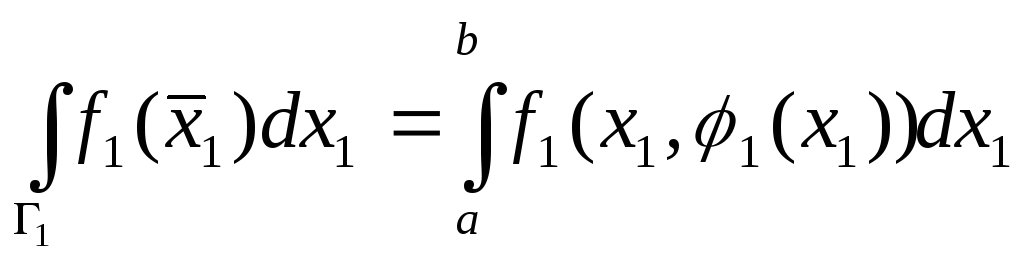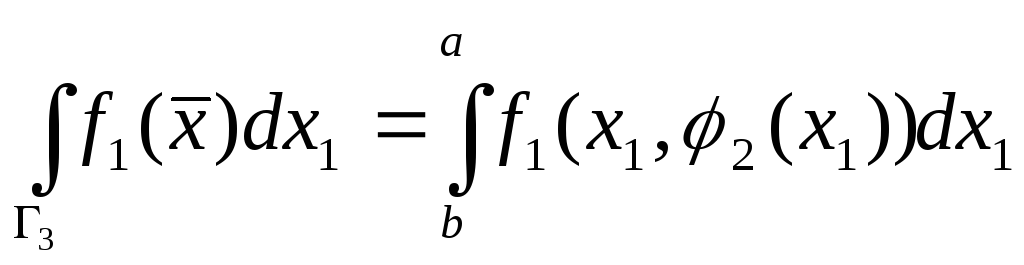