§ 7. Тройные интегралы.

Изложенная теория двойного интеграла без каких-либо осложнений и новых идей переносится на случай тройного интеграла. Остановимся лишь на формуле повторного интегрирования для тройного интеграла.

Пусть – плоская область, ограниченная кусочно-гладкой кривой и–цилиндрический брус, ограниченный снизу - поверхностью,сверху -поверхностью,, с боку - цилиндрической поверхностью с образующей, параллельной осии направляющей-границей области.

Если функция непрерывна в, то справедливо равенство

.

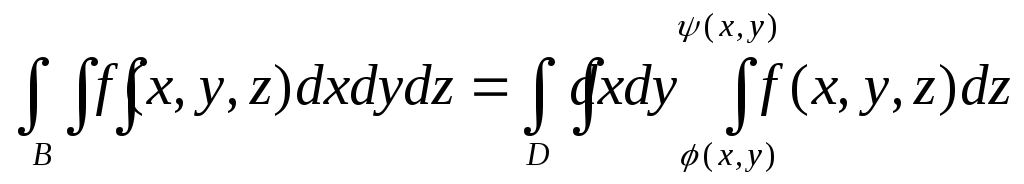§ 8. Замена переменных в двойном и тройном интегралах.

Формула замены переменных является одним из важнейших средств вычисления кратных интегралов.

1) Замена переменных в двойном интеграле.

Предположим, что функция интегрируема в области. Предположим далее, что от переменныхмы переходим к переменным, то есть совершаем преобразование

; (*)

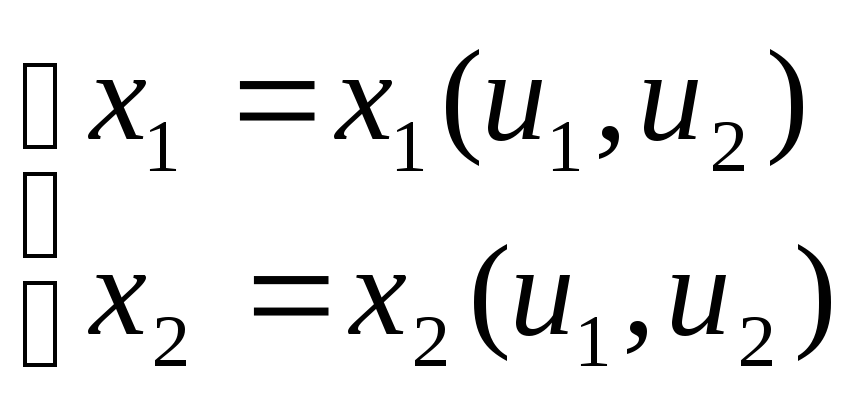Обозначим через ту область в, которая при преобразовании (*) переводится в.

Теорема 1.

Если преобразование (*) переводит область ви является взаимно однозначным и если функции (*) имеют внепрерывные частные производные первого порядка по всем переменным и отличный от нуля якобиан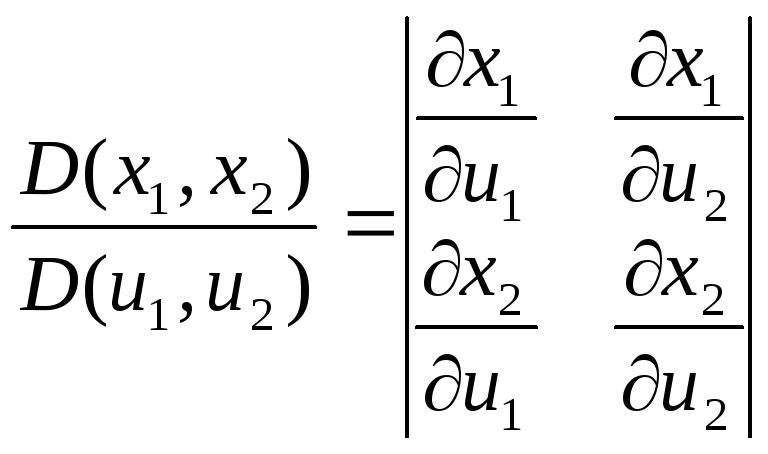, то для каждой интегрируемой вфункциисправедлива формула замены переменных:

.

Замечание 1. В условиях теоремы можно допустить обращение в нуль якобиана на некотором принадлежащем множестве точек, имеющем площадь нуль, а также допустить неоднозначность отображения на таком же множестве.

Наиболее часто при вычислении двойных интегралов переходят от декартовых к полярным координатам.

, ,,.

.

2) Замена переменных в тройном интеграле.

В случае тройных интегралов справедлива аналогичная теорема. Отметим две наиболе важных замены переменных.

1. Сферические координаты.

, ,,

.

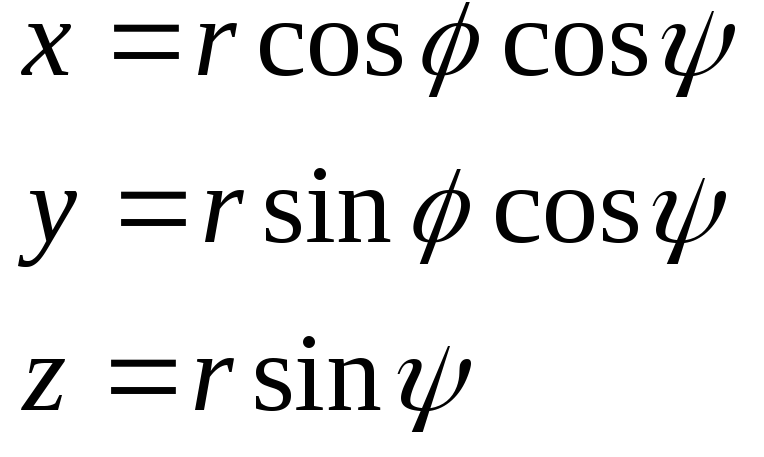2. Цилиндрические координаты.

, ,,

.

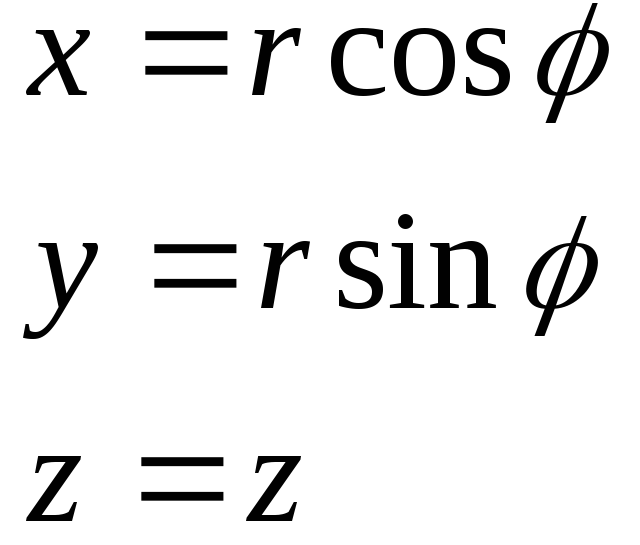§ 9. Криволинейные интегралы.

Физический смысл производной дает возможность определить понятие «длины траектории», заданной уравнением . Назовем траекторией Г множество значений вектор-функциина отрезке, а черезобозначим дугу траектории Г, соответствующей отрезку времени. Допустим, что вектор-функциянепрерывна на отрезкеи обозначим черезфункцию, обладающую свойствами:и, для всех. С физической точки зренияесть величина (модуль скорости движения точки и поэтому значения функцииестественно считать длиной пройденного пути за отрезок времени, то есть длиной дуги. Функциюможно задать равенством:

, .

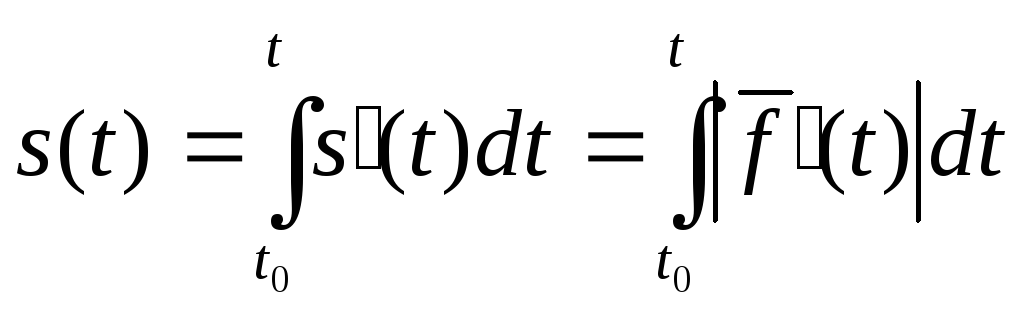Поэтому число

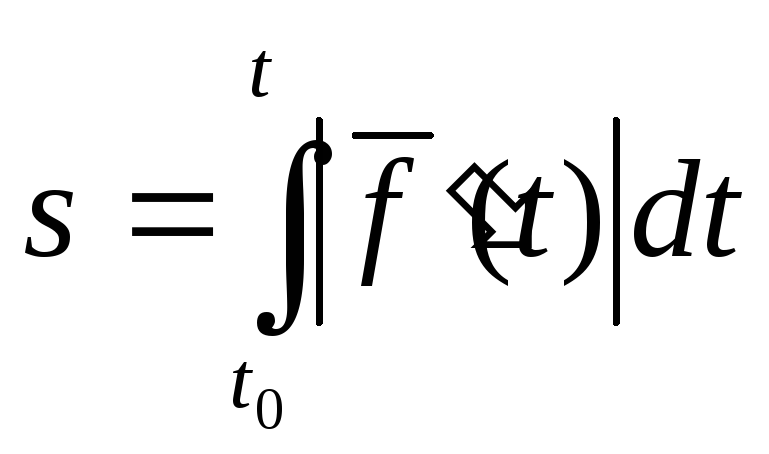
Называют длиной траектории Г, или длиной годографа вектор-функции . С этим понятием связано понятие криволинейного интеграла 1-го типа.

Определение. Пусть вектор-функция имеет на отрезкенепрерывную производную. Пусть функцияопределена на множестве Г. Тогда интеграл

,

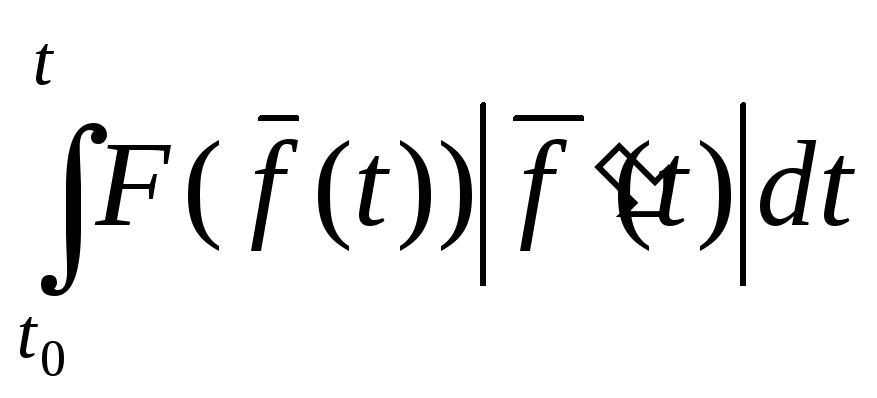если он существует, называется интегралом от функции по длине дуги траектории Г и обозначается. Этот интеграл называют также криволинейным интегралом 1-го типа.

Криволинейному интегралу 1-го типа можно дать физическое истолкование. Прежде всего, напомним, что если материальная точка единичной массы перемещается из точки в точкупод действием постоянной силы. Если действующая сила не является постоянной, а зависит от положения точки, то производимую работу естественно считать по формуле

.

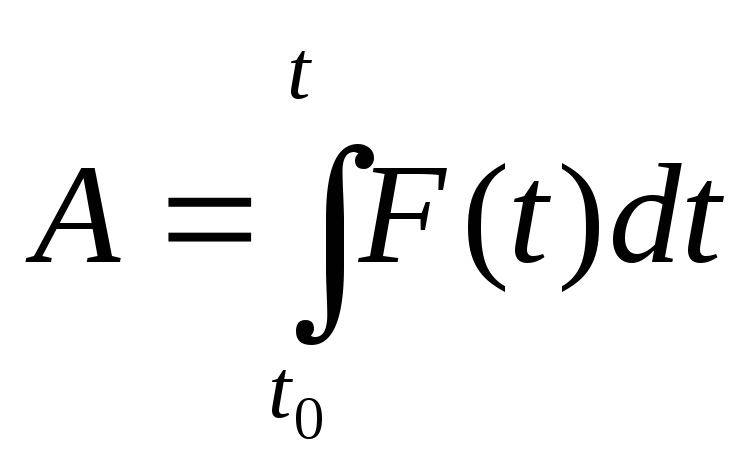В обоих этих примерах мы считали, что действующая сила направлена в сторону движения точки. Пусть теперь материальная точка единичной массы перемещается вдоль траектории Г, заданной уравнением ,, под действием силы, зависящей от положения точки и направленной вдоль Г, то есть в направлении вектора. Тогда эта материальная точка производит работу, которую можно вычислить по формуле

.

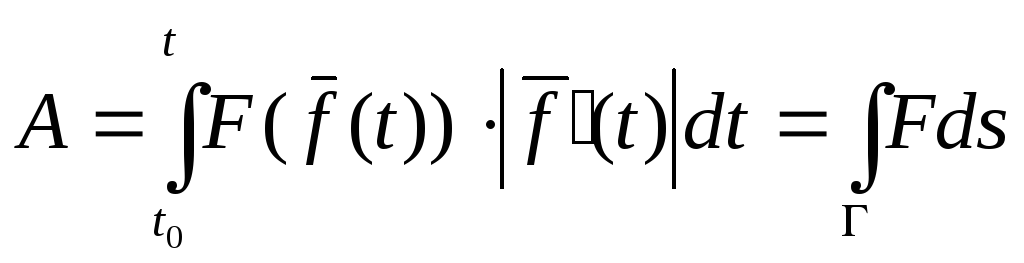Таким образом, криволинейный интеграл 1-го типа можно истолковать как работу, производимую при перемещении точки вдоль траектории Г под действием силы , направленной по касательной к Г.

Ту же задачу вычисления работы, которую производит перемещающаяся точка, можно решать с векторной точки зрения. Пусть материальная точка единичной массы под действием постоянного вектора силы перемещается вдоль вектора, то есть перемещается, например, из начала координат в точку с координатами. Как известно, при этом будет произведена работа. Пусть теперь вектор силы зависит от положения точки на векторе. Обозначим координаты векторадля удобства через. Тогда можно считать, что. Работу, которую производит перемещающаяся точка, естественно вычислять по формуле

Здесь через обозначен векторПусть, наконец, материальная точка единичной массы перемещается вдоль траектории Г, заданной уравнением,, под действием силы, зависящей от положения точки. Тогда эта материальная точка производит работу, которую можно вычислить по формуле

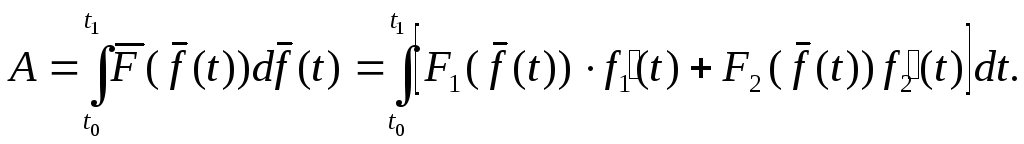
С этим понятием работы связано понятие криволинейного интеграла 2-го типа.

Определение. Пусть вектор-функция имеет на отрезкенепрерывную производную и пусть Г есть годограф вектор-функцииили, другими словами, траектория, заданная уравнением,. Пусть вектор-функцияопределена на множестве Г.

Тогда интеграл

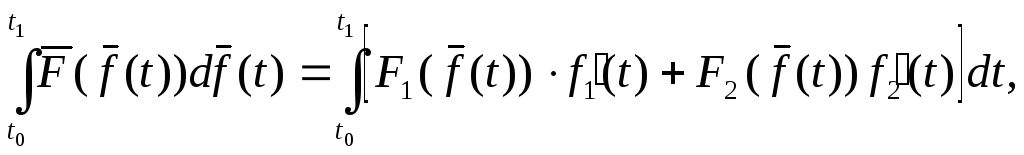
Если он существует, называется криволинейным интегралом 2-го типа от вектор-функции по траектории Г и обозначается

, или .

Как видим физическое истолкование криволинейных интегралов 1-го и 2-го типов отличается лишь тем, что в первом случае работа вычисляется при условии, что действующая сила направлена по касательной к траектории Г, а во втором случае вектор силы имеет произвольное направление. Разумеется, нетрудно свести один случай к другому. В самом деле, если вектор силы, а траектория Г имеет касательную, составляющую с осями координат углыи, то в направлении этой касательной будет действовать сила величиной. Это дает повод установить связь между криволинейными интегралами 1-го и 2-го типа.

Теорема. Пусть вектор-функция имеет на отрезкенепрерывную производнуюи пусть Г есть траектория, заданная уравнением,. Пусть вектор-функциянепрерывна на можестве Г. Тогда имеет место равенство

,

где и- это углы, образуемые касательной к траектории Г с координатными осямии, причем направление касательной соответствует возрастанию дуг траектории от точкидо точки.

Доказательство. Прежде всего заметим, что в силу непрерывности вектор-функции оба криволинейных интеграла, указанных в теореме существуют. Далее, еслии- это углы, указанные в теореме, то они вычисляются из соотношений

, ,

где - единичные векторы, соответствующие координатным осями. Отсюда следует, что

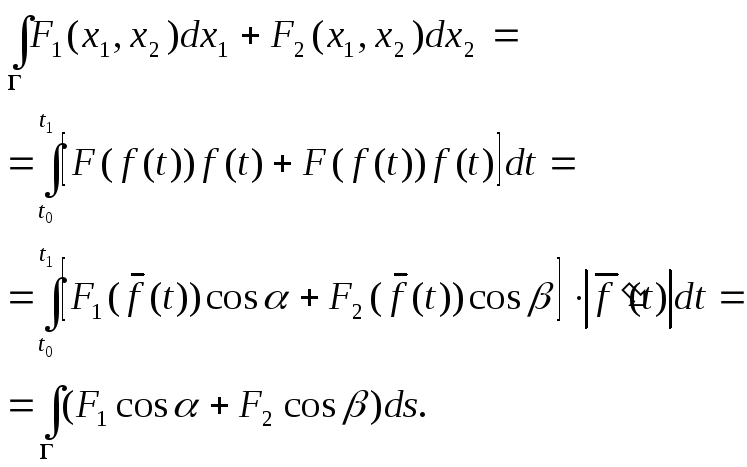
Теорема доказана.