§ 4. Интеграл Римана от ограниченной финитной функции.

В этом параграфе так же, как для случая функций одного переменного, определим понятие интегрируемости в смысле Римана-Дарбу функции, введем интеграл Римана и рассмотрим его свойства.

Определение. Ограниченная финитная функция называется интегрируемой в смысле Римана-Дарбу на плоскости, если.

Отметим, что число называется нижним интегралом функциии обозначается символом. Нижний интеграл мог быть определен иначе:

.

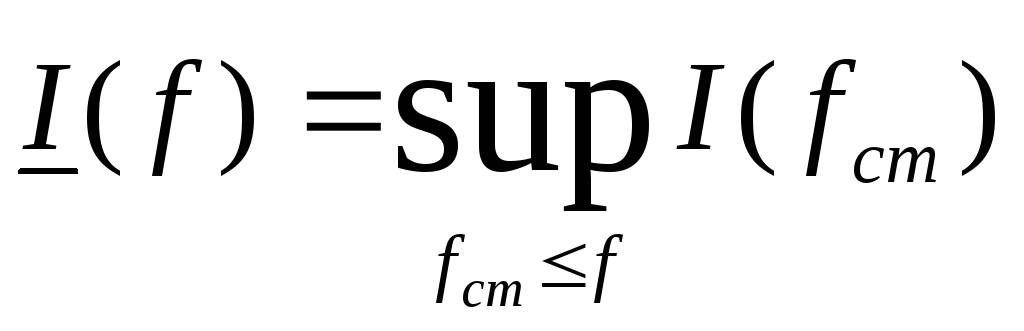Если бы удалось определить интеграл , продолжая интеграл с класса ступенчатых функций и сохраняя свойства интеграла, то числовсегда было бы оценкой сверху для, а числобыло бы оценкой снизу для. Интегрируемость функциив смысле Римана-Дарбу представляет собой такое свойство функции, которое обеспечивает равенство оценок снизу и сверху для интеграла функции, если бы он был определен. Поэтому естественно звучит следующее определение интеграла.

Определение 2. Пусть -ограниченная финитная функция, интегрируемая в смысле Римана-Дарбу. Тогда числоназывается интегралом, или интегралом Римана от функциии обозначается одним из символов:

, ,,,.

Приведем критерий интегрируемости функции в смысле Римана-Дарбу.

Теорема 1. Ограниченная финитная функция интегрируема в смысле Римана-Дарбу тогда и только тогда, когда для любогонайдутся ступенчатые функцииитакие, что

и .

Доказательство. Докажем сначала достаточность условий теоремы. Пользуясь свойством выпуклости верхнего интеграла, свойством линейности интеграла от ступенчатых функций и условиями теоремы, запишем:

,

То есть . В силу ипроизвольностииз последнего неравенства следует, что, и, значит, функцияинтегрируема в смысле Римана-Дарбу.

Докажем теперь необходимость условий теоремы. Пусть функция интегрируема в смысле Римана-Дарбу. По определению верхнего интеграладля всякогонайдется ступенчатая функциятакая, чтои. Так как, то из приведенных неравенств следует, что, где. Теорема доказана.

Пусть дана ограниченая финитная функция . При каждом фиксированном значении переменногообозначим черезверхний интеграл от значений функциипо переменному(по прямой), а через-верхний интеграл от значений функциипо второму переменномупри фиксированном значении первого переменного. Сравнительно просто решается задача о сведении двойного интеграла Римана к повторным интегралам.

Теорема 2. Если ограниченная финитная функция интегрируема на плоскостив смысле Римана-Дарбу, то функциииинтегрируемы на прямойи справедливы равенства:

.

Доказательство. Для всякого найдутся ступенчатые функции функцииитакие, чтои. Зафиксируем. Тогда для всех, за исключением, быть может, конечного числа точек, справедливы неравенства. Воспользовавшись монотонностью верхнего интеграла по переменному, получим

.

Легко видеть, что крайние части неравенств представляют собой значения ступенчатых функций, зависящих от одного переменного . Кроме того,

.

Следовательно, значения функции интегрируемы по переменномуна прямойи справедливы неравенства:

.

Отсюда и из неравенства

заключаем, что

.

В силу произвольности это означает, что

.

Совершенно аналогично доказывается равенство

.

Теорема доказана.

Следствие 1. Если ограниченная финитная функция интегрируема в смысле Римана-Дарбу на плоскости, а при всех, за исключением, быть может, конечного числа значений, интегрируема в смысле Римана-Дарбу по переменномуна прямой, то повторный интеграл

существует и равен двойному интегралу от функции .

Следствие 2. Если ограниченная финитная функция интегрируема в смысле Римана-Дарбу на плоскости, а при всех, за исключением, быть может, конечного числа значений, интегрируема в смысле Римана-Дарбу по переменномуна прямой, то повторный интеграл

существует и равен двойному интегралу от функции .

Следствие 3. Если одновременно выполнены условия следствий 1 и 2, то оба повторных интеграла существуют и равны двойному интегралу от функции , то есть

.

Доказательства следствий 1-3 получаются, если в теореме 2 верхний интеграл заменить на интеграл(следствие 1), а верхний интегралзаменить на интеграл(следствие 2). Следствие 3 объединяет следствия 1 и 2.

Определение 1. Назовем элементарной фигурой множество точек, представляющих собой объединение конечного числа прямоугольников со сторонами, параллельными осям координат.

Определение 2. Будем говорить, что ограниченная финитная функция обладаетI-свойством, если для любого найдется элементарная фигура площади, меньшей, содержащая все точки и линии разрыва функции.

Замечание. Множество точек плоскости назовем множеством площади нуль, если оно содержится в элементарной фигуре (или многоугольной фигуре) сколь угодно малой площади.

Теорема 1. Если ограниченная финитная функция обладаетI-свойством, то она интегрируема на плоскости в смысле Римана-Дарбу.

Доказательство . Пусть и-верхняя и нижняя грани функциии. Покроем точки линиями разрыва функцииконечным числом прямоугольников, сумма площадей которых меньше. Возьмем замкнутый прямоугольник, содержащий эту элементарную фигуру и носитель функции. Точки прямоугольника, не принадлежащие указанной элементарной фигуре, образуют множество, состоящее из конечного числа непересекающихся прямоугольников. Назовем их дополнительными. На каждом таком замкнутом прямоугольнике функци енпрерывна, а следовательно, и равномерна непрерывна. Значит существуют такие числа, что если, тодля всех, принадлежащихi-му дополнительному прямоугольнику.

Пусть . Тогда если взять разбиение дополнительных прямоугольников на частичные прямоугольники так, чтобы длина диагонали каждого из них не превосходила, то разность между верхней граньюи нижней граньюфункциинаk-ом прямоугольнике будет не больше .

Объединяя все разбиения дополнительных прямоугольников и прямоугольников построенной элементарной фигуры, определим

и

.

Тогда ,

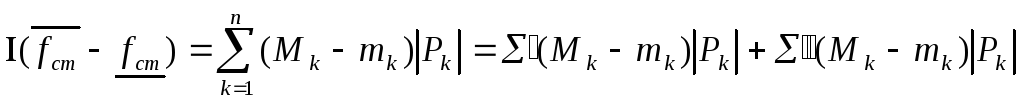где в сумму отнесены слагаемые, отвечающие прямоугольникам, покрывающим точки разрыва, а в сумму-все остальные.

Поскольку для любогоk, то

.

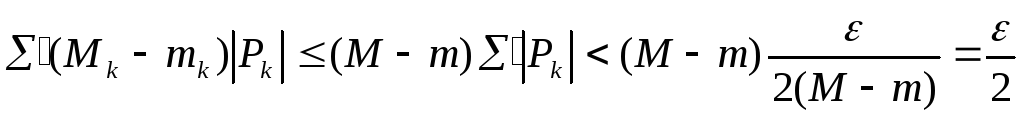Далее,

.

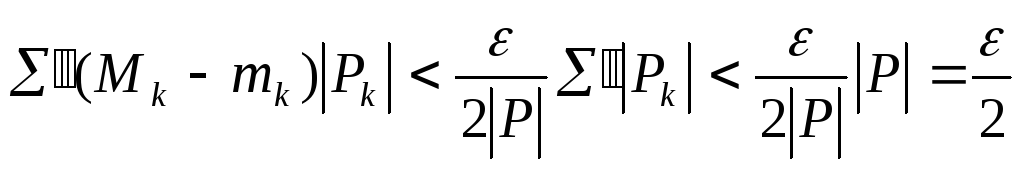Таким образом,

.

Согласно критерию интегрируемости, функция f интегрируема.