3.Бінарні відношення. Основні операції над бінарними відношеннями.
Бінарне відношення (бінарне відношення на множині) — в математиці окремий випадок відношення на множині, яке встановлюється між двома елементами множини.Кажуть також, що елементи a,b ∈ M знаходяться у бінарному відношенні R (часто записують у вигляді aRb), якщовпорядкована пара (a,b) ∈ R. Отже, R є підмножиною декартового квадрата: R⊆ M×M.Іноді розрізняють поняття бінарного відношення на множині та бінарного відношення між множинами, яке в цій енциклопедії називається відповідністю між множинами.
Види відношень
Рефлексивне транзитивне відношення називається відношенням квазіпорядка .
Рефлексивне симетричне транзитивне відношення називається відношенням еквівалентності .
Рефлексивне антисиметричне транзитивне відношення називається відношенням ( часткового ) порядку .
Антирефлексивне антисиметричне транзитивне відношення називається відношенням строгого порядку .
Повне антисиметричне ( для будь-яких x , y виконується xRy або yRx ) транзитивне відношення називається відношенням лінійного порядку .
Антирефлексивне антисиметричне відношення називається відношенням домінування.
Операції з відношеннями
Оскільки відношення на M є також множинами, то над ними дозволені теоретико-множинні операції. Наприклад:
перетином бінарних відношень "більше або дорівнює" і "менше або дорівнює" є відношення "дорівнює",
об’єднанням відношень "менше" і "більше" є відношення "не дорівнює",
доповненням відношення "ділиться на" є відношення "не ділиться на" тощо.
5. Властивості бінарних відношень.
Нехай R — деяке відношення на множині M. Відношення R називається
Обернене відношення (відношення , зворотне до R ) - це бінарне відношення , що складається з пар елементів ( у, х ) , отриманих перестановкою пар елементів ( х , у) даного відношення R. Позначається: R−1. Для даного відношення і зворотного йому вірно рівність : (R−1)−1 = R.
Взаємообернене відношення - відносини, що є зворотними один по відношенню до одного. Область значень одного з них служить областю визначення іншого , а область визначення першого - областю значень іншого.
рефлексивним, якщо для всіх a∈M має місце aRa.
Бінарне відношення R , визначене на деякій множині і відрізняється тим , що для будь-якого х цієї множини елемент х знаходиться у відношенні R до самого себе , тобто для будь-якого елемента х цієї множини має місце xRx . Приклади рефлексивних відносин : рівність , одночасність , подібність.
антирефлексивним (іррефлексивним), якщо для жодного a∈M не виконується aRa. Іррефлексивне ставлення , відзначимо , що так само , як антисиметричність не збігається з несиметричною , іррефлексівність не збігається з нерефлексивному . ) - Двомісне відношення R , визначене на деякій множині і відрізняється тим , що для будь-якого елемента х цієї множини невірно , що воно знаходиться у відношенні R до самого себе (невірно , що xRx ) , тобто можливий випадок , що елемент множини не знаходиться у відношенні R до самого себе. Приклади нерефлексвних відносин : « дбати про » , « розважати » , « нервувати ».
симетричним, якщо для всіх a,b∈M таких, що aRb маємо bRa. Бінарне відношення R , визначене на деякій множині і відрізняється тим , що для будь-яких елементів х і у цього безлічі з того , що х знаходиться к у відносно R ( xRy ) , випливає, що і у знаходиться в тому ж відношенні до х ( уRx ) . Прикладом симетричних відносин можуть бути рівність ( =) , відношення еквівалентності , подібності , одночасності , деякі відносини споріднення .
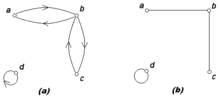
Симетричне відношення
асиметричним, якщо для всіх a,b∈M таких, що aRb не виконується bRa. Бінарне відношення R , визначене на деякій множині і відрізняється тим , що для будь-яких х и у з xRy слід \ neg yRx . Приклад : ставлення «більше» ( > ) і « менше» (<) .
антисиметричним, якщо для всіх a,b∈M таких, що aRb і bRa маємо a = b. Бінарне відношення R , визначене на деякій множині і відрізняється тим , що для будь-яких х и у з xRy і xR - 1y слід х = у (тобто R і R- 1 виконуються одночасно лише для рівних між собою членів).
транзитивним, якщо зі співвідношень aRb і bRc випливає aRc. Бінарне відношення R , визначене на деякій множині і відрізняється тим , що для будь-яких х , у, z цієї множини з xRy і yRz слід xRz ( xRy & yRz \ toxRz ) . Приклади транзитивних відносин : «більше» , «менше» , «дорівнює» , « подібно » , «вище» , « північ ».
Нетранзитивне - бінарне відношення R , визначене на деякій множині і відрізняється тим , що для будь-яких х , у, z цієї множини з xRy і yRz не слід xRz ( \ ( xRy & yRz \ toxRz )) . Приклад нетранзитивного відношення: « x батько y »
повним, якщо для будь-яких a,b∈M випливає, що aRb або bRa.
Відношення порядку - відношення, що володіє тільки деякими з трьох властивостей відношення еквівалентності . Зокрема , ставлення рефлексивне і транзитивне , але несиметричне (наприклад , « не більше» ) утворює « нестрогий » порядок . Ставлення Транзитивне , але нерефлексівное і несиметричне (наприклад , «менше» ) - « суворий» порядок.
Функція - бінарне відношення R , визначене на деякій множині , яке відрізняється тим , що кожному значенню x відносини xRy відповідає лише одне - єдине значення y . Приклад : « y батько x ». Властивість функціональності відносини R записується у вигляді аксіоми : ( xRy і xRz ) → ( y ≡ z ) . Оскільки кожному значенню x у виразах xRy і xRz відповідає одне і те ж значення , то y і z збіжаться , виявляться одними і тими ж. Функціональне ставлення однозначно , оскільки кожному значенню x відносини xRy відповідає лише одне - єдине значення y , але не навпаки.
Бієкція - бінарне відношення R , визначене на деякій множині , яке відрізняється тим , що в ньому кожному значенню х відповідає єдине значення у, і кожному значенню у відповідає єдине значення х . Одно- однозначне ставлення є окремим випадком однозначного ставлення .
Відношення зв'язку - це бінарне відношення R , визначене на деякій множині , яке відрізняється тим , що для будь-яких двох різних елементів х и у з цієї множини , одне з них знаходиться у відношенні R до іншого ( тобто виконано одну з двох співвідношень : xRy або yRx ) . Приклад : ставлення «менше» (<)
Якщо відношення R має будь-яку з перерахованих вище властивостей, то обернене відношення R−1 також має ту саму властивість. Таким чином, операція обернення зберігає всі ці властивості відношень.
Відношення, яке є рефлексивним, симетричним та транзитивним, називається відношенням еквівалентності.