Savchenko_O_Ya__FMSh_NGU__Zadachi_po_fizike

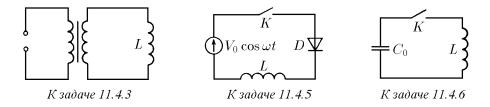
жением 40 В напряжение на катушке 2 равно 10 В. Какое напряжение будет на разомкнутых зажимах катушки 1, если катушку 2 включить в цепь переменного тока с напряжением 10 В?

11.3.25 . Имеются два одинаковых идеальных трансформатора с одинаковым коэффициентом трансформации 1 : 3. Первичная обмотка одного из них соединена последовательно со вторичной второго, и свободные концы этих обмоток включены в сеть переменного тока с напряжением 100 В. Вторичная обмотка первого трансформатора последовательно соединена с первичной обмоткой второго. Определите амплитуду переменного напряжения между другими концами обмоток.

§ 11.4. Электрические цепи переменного тока

11.4.1.Батарея без внутреннего сопротивления подключена к соленоиду индуктивности L. Определите зависимость тока в цепи от времени, если ЭДС батареи E. Найдите работу батареи за время τ. В какой вид энергии превращается эта работа?

11.4.2.Как должно меняться напряжение в электрической цепи, состоящей из последовательно соединенных катушки индуктивности L и сопротивления R, чтобы ток в ней: а) линейно возрастал: I = αt? б) менялся синусоидально: I =

I0 sin ωt?

♦11.4.3 . При переходе вещества в сверхпроводящее состояние только небольшая часть электронов проводимости движется, не испытывая при этом сопротивления. Ток в сверхпроводящем соленоиде индуктивности L «запускают», подключая к соленоиду на время t постоянное напряжение. Максимальный ток в соленоиде I. Определите верхний предел количества теплоты, выделяющейся в соленоиде при запуске в нем тока. Перед переходом в сверхпроводящее состояние сопротивление соленоида было R.

11.4.4 . Генератор с ЭДС E = E0 sin ωt в момент t = 0 подключают к катушке индуктивности L. Определите зависимость тока в цепи от времени. Активным сопротивлением цепи можно пренебречь. Объясните полученный результат.

♦11.4.5. В схеме, показанной на рисунке, диод D и катушка индуктивности L при помощи ключа K подключаются к источнику переменного напряжения V =

V0 cos ωt. В момент времени t = 0 ключ K замыкается. Определите силу тока в катушке как функцию времени. Постройте график этой функции. Диод и катушку считать идеальными. Внутренним сопротивлением источника пренебречь.

♦11.4.6. В цепи, состоящей из заряженного конденсатора емкости C0 и катушки индуктивности L, замыкают ключ K. По какому закону должна изменяться во времени емкость конденсатора, чтобы ток в цепи нарастал прямо пропорционально времени?

♦ 11.4.7. В изображенной на рисунке цепи конденсатор емкости C заряжен до напряжения V0. Сначала замыкают ключ K1. В момент, когда ток через катушку

231

индуктивности L достигает своего максимального значения, замыкают ключ K2 и размыкают ключ K1. Каким оказывается наибольшее значение напряжения на сопротивлении R?

11.4.8.а. В какой момент искрит рубильник — при замыкании или при размыкании? Почему искрение прекращается, если параллельно рубильнику включить конденсатор?

б. Какой емкости конденсатор нужно подсоединить параллельно катушке индуктивности L, чтобы при размыкании ключа напряжение на ней не увеличилось более чем в N раз, если частота напряжения в цепи ν? Определите эту емкость

вслучае ν = 50 Гц, L = 0, 1 Гц, N = 10.

11.4.9.Источник с ЭДС E и нулевым внутренним сопротивлением в момент времени t = 0 подключают к последовательно соединенным катушке индуктивности L и конденсатору емкости C. Найдите максимальный ток в цепи и максимальный заряд конденсатора.

♦ 11.4.10. Найдите максимальный ток в катушках индуктивности L1 и L2 после замыкания ключа K в цепи, изображенной на рисунке. Емкость конденса-

тора C, начальное напряжение на нем V .

♦ 11.4.11 . В схеме, изображенной на рисунке, в момент времени t = 0 замыкают ключ K. Определите ток в цепи, если источник дает: а) постоянное напряжение V0; б) косинусоидальное напряжение V0 cos ωt. Определите максимальный

ток, если V0 = 100 В, L = 10−2 Гн, C = 10−3 Ф, ν = ω/2π = 50 Гц.

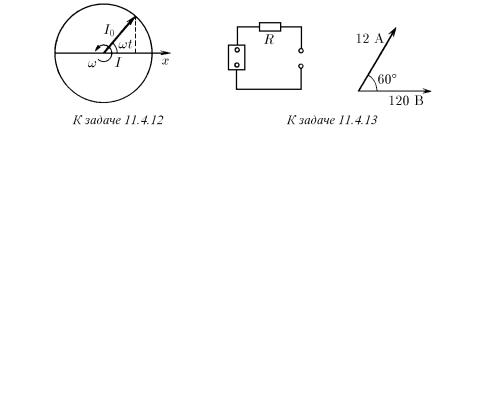
♦11.4.12. а. На векторной диаграмме ток I = I0 cos ωt определяется как проекция на ось x вектора I0, который вращается вокруг точки O с угловой скоростью ω. Как расположены на этой же диаграмме векторы падения напряжения при протекании этого тока через сопротивление R, катушку индуктивности L и конденсатор емкости C? Чему равны амплитуды векторов напряжения?

б. Используя векторную диаграмму, определите падение напряжения в цепи последовательно соединенных катушки индуктивности L, сопротивления R и конденсатора емкости C и сдвиг фаз между током и напряжением в цепи, если ток в цепи меняется косинусоидально: I = I0 cos ωt.

♦11.4.13. Значения напряжения, тока и сдвига фаз между напряжением и током в цепи нагрузки показаны на векторной диаграмме. Определите амплитуду ЭДС источника, если R = 10 Ом.

♦11.4.14. Найдите установившийся ток в цепи, изображенной на рисунке.

232

♦ 11.4.15. Подберите индуктивность дросселя так, чтобы амплитуда напряжения на выходе фильтра при частоте 100 Гц была в 10 раз меньше амплитуды

♦11.4.16 . Имеется фазовращательная цепь. К клеммам A и B подводится

напряжение V = V0 sin ωt. Какое напряжение снимается с клемм M и N при

R0C0 = RC?

♦ 11.4.17. Найдите установившиеся токи в электрических цепях, изображенных на рисунке. Внутреннее сопротивление источников напряжения равно нулю. Определите среднюю мощность, выделяющуюся в цепях, если E0 = 200 В, R = 100 Ом, C = 10−4 Ф, L = 1 Гн. Частота напряжения источника ν = ω/2π = 50 Гц.

11.4.18.Последовательно с электроплиткой в городскую сеть подключили катушку индуктивности. При этом мощность плитки упала в два раза. Найдите индуктивность катушки, если активное сопротивление плитки 50 Ом.

11.4.19.Электрическая цепь, состоящая из двух катушек индуктивности и лампочки, подключена к генератору переменного напряжения. Если в одну из катушек вдвинуть железный сердечник, то свечение лампочки усиливается, если же сердечник вдвинуть во вторую катушку, то свечение лампочки ослабевает. Составьте схему возможной электрической цепи.

♦11.4.20 . Начальное напряжение на конденсаторе емкости C0 равно V0, а конденсатор емкости C не заряжен. Через какое время после замыкания ключа K пробьется конденсатор емкости C, если его пробой происходит при напря-

♦ 11.4.21. а. Докажите, что в двух параллельно соединенных катушках индуктивности L1 и L2 сумма L1I1 +L2I2 не меняется. Направление токов показано на рисунке.

233

♦б. Конденсатор емкости C, заряженный до напряжения V0, разряжается через катушку индуктивности L1. Какой максимальный ток можно получить в катушке индуктивности L2, если замкнуть ключ K в момент, когда ток индуктивности L1 максимален?

♦11.4.22 . а. В момент, когда ток в катушке индуктивности L1 был равен I, ключ K замкнули. Какое количество теплоты выделится на сопротивлении R после замыкания ключа?

б. При замкнутом ключе K ток в катушке индуктивности L1 равен I1, а в индуктивности L2 равен I2. Определите, в каких пределах будет меняться ток в катушках индуктивности L1 и L2 после размыкания ключа K.

11.4.23 . Из-за наличия активного сопротивления проводов в колебательном контуре, состоящем из конденсатора емкости 1 мкФ и катушки индуктивности 1 мкГн, амплитуда тока за 1 мс уменьшилась в два раза. Определите сопротивление проводов.

♦ 11.4.24 . В колебательном контуре, состоящем из последовательно соединенных сопротивления R, катушки индуктивности L и конденсатора емкости C, происходят затухающие колебания. За некоторое время амплитуда тока в контуре уменьшилась от значения I1 до значения I2. Какое количество теплоты выделилось за это время на сопротивлении?

♦ 11.4.25 . При распространении синусоидальных волн в бесконечной LCцепочке фаза колебаний напряжения в каждом узле отстает на ϕ от фазы колебаний в предшествующем узле. Определите зависимость ϕ от ω, L, C. Чему равна скорость распространения синусоидальной волны по LC-цепочке, если длина ячейки l? Чему равна эта скорость при малых ω?

§11.5. Сохранение магнитного потока. Сверхпроводники в магнитном поле

11.5.1. Почему при деформации сверхпроводящего кольца с током полный магнитный поток через кольцо сохраняется?

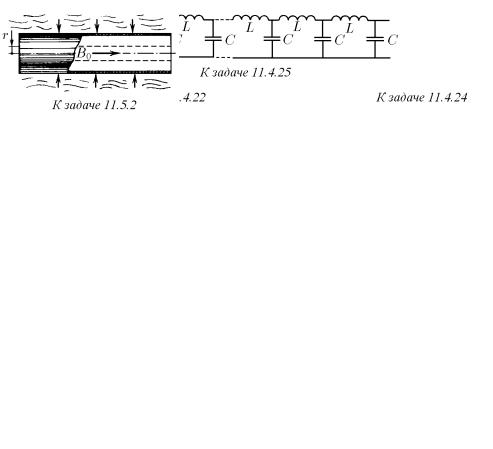
♦ 11.5.2. Длинную цилиндрическую металлическую оболочку радиуса r0, которая находилась в постоянном магнитном поле индукции B0, сжали взрывом. Определите индукцию магнитного поля внутри сжатой оболочки, если ее радиус стал равным r. Активным сопротивлением оболочки пренебречь.

234

11.5.3.Во сколько раз изменится ток в двух удаленных друг от друга тонких сверхпроводящих кольцах с однонаправленным током при их совмещении?

11.5.4.Когда в короткозамкнутый сверхпроводящий длинный соленоид с током вставили сверхпроводящий стержень, ток в соленоиде увеличился в три раза. Определите, во сколько раз сечение соленоида больше сечения стержня.

11.5.5.Короткозамкнутый длинный соленоид с током I, сделанный из сверхпроводника, сжали так, что его длина уменьшилась в три раза. Как изменится ток в соленоиде? Шаг витка соленоида много меньше его радиуса.

♦11.5.6 . Длинный короткозамкнутый сверхпро-

водящий соленоид вдвигают в магнитное поле индукции B0 под углом α к направлению поля. Как распределится индукция магнитного поля в соленоиде, если он лишь наполовину войдет во внешнее поле?

11.5.7.Сверхпроводящее кольцо индуктивно-

сти L, в котором течет ток I0, вносят в однородное магнитное поле индукции B0. Найдите ток, который

будет протекать по кольцу. Нормаль к плоскости кольца составляет с направлением поля угол α; радиус кольца r.

11.5.8.В постоянном однородном поле индукции B вокруг своего диаметра, ориентированного перпендикулярно полю, вращается сверхпроводящее кольцо. Индуктивность кольца L, его диаметр D. Определите амплитуду переменного тока в кольце.

11.5.9.Длинный короткозамкнутый сверхпроводящий соленоид соосно надели на еще более длинный стальной цилиндр, сечение которого в два раза меньше сечения соленоида. На сколько изменится индукция магнитного поля вне и внутри части стального цилиндра, находящейся внутри соленоида, если магнитное

поле соленоида много больше магнитного поля насыщения стали B0?

11.5.10 . Сквозь катушку сечения S и длины h, изготовленную из сверхпроводящей проволоки, пролетает с постоянной скоростью сверхпроводящий стержень сечения σ и длины l. Начертите график зависимости тока в катушке от

положения стержня, если катушка замкнута накоротко и начальный ток в ней I0. Рассмотрите случаи: а) l > h; б) l < h. Краевыми эффектами пренебречь.

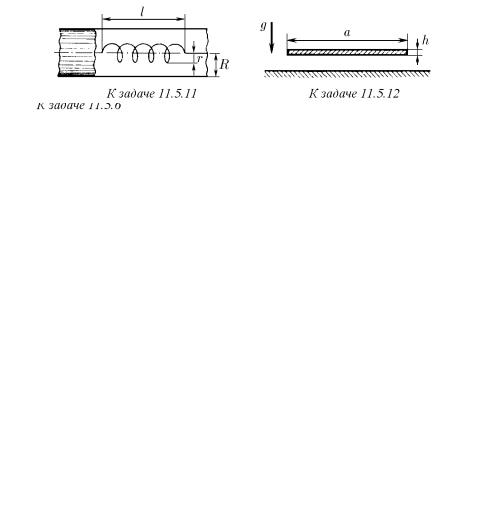
♦11.5.11 . Вычислите индуктивность длинного соленоида радиуса r и длины l, помещенного внутрь длинной сверхпроводящей трубы радиуса R вдоль ее оси. Число витков соленоида N.

♦11.5.12. Плоская медная шина, сечение которой a×h = 100×1 мм, параллельна горизонтальной поверхности сверхпроводника. Какой ток нужно пропускать через шину, чтобы она не падала на сверхпроводник?

11.5.13 . Через длинный прямой провод, который находится на высоте h над сверхпроводящей плоскостью, пропустили ток I. Чему равно максимальное магнитное давление на поверхность сверхпроводника? С какой силой действует сверхпроводник на единицу длины провода?

235

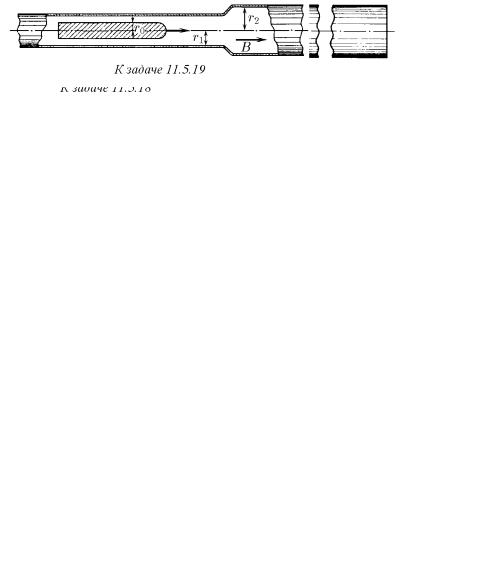
11.5.14. Длинный соленоид с разомкнутыми концами расположен вдоль постоянного магнитного поля с индукцией B = 2 Тл. Число витков на единицу длины соленоида n = 1000 м−1. С какой скоростью пролетел сквозь этот соленоид длинный металлический снаряд радиуса r = 9 см, если максимальное напряжение, которое появилось на концах соленоида, V = 100 кВ? Сопротивлением металла снаряда пренебречь.

11.5.15 . Почему ответ задачи 11.5.14 не зависит от формы концов снаряда?

♦11.5.16 . Когда цилиндрический металлический снаряд массы m, длины l и радиу-

са r, летящий со скоростью v0, находился внутри соленоида с числом витков N, длиной L и радиусом R l, в соленоиде создали ток I, а затем его цепь закоротили. На сколько увеличится скорость снаряда, вылетевшего из соленоида? Сопротивлением металла пренебречь.

♦11.5.17 . На большом расстоянии от длинной сверхпроводящей круглой трубы радиуса r соосно с ней расположена короткозамкнутая сверхпроводящая катушка с током I. Число витков в катушке N, длина катушки l r, радиус r/2, масса катушки m. Какую скорость нужно сообщить катушке, чтобы она пролетела сквозь закрепленную трубу?

♦ 11.5.18 . Какой минимальной скоростью должен обладать сверхпроводящий тонкий стержень сечения S, длины l и массы m, чтобы влететь в продольное магнитное поле индукции B?

♦ 11.5.19. Длинная металлическая трубка, имеющая участок радиуса r1 и участок радиуса r2, помещена вдоль однородного магнитного поля индукции B. На сколько изменится энергия сверхпроводящего снаряда радиуса r0 и длины l r1, r2, летящего по оси трубки, при пересечении им границы между участками трубки различного радиуса? Влиянием сопротивления металла на процесс взаимодействия снаряда с трубкой пренебречь.

♦ 11.5.20. Двухканальный магнитный перераспределитель энергии снарядов имеет следующую конструкцию. Две металлические трубы с прорезью соедине-

236

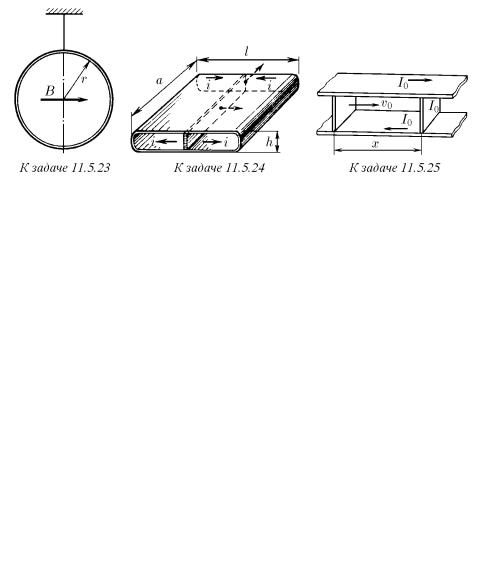
ны металлическими перемычками так, как изображено на рисунке. Однородное магнитное поле индукции B направлено вдоль оси труб. Вдоль оси каждой трубы движутся одинаковые длинные сверхпроводящие снаряды. Один из снарядов, имеющий скорость 3v, догоняет второй снаряд, имеющий скорость v. Длина каждого снаряда l, сечение s, масса m. Сечение каждой трубы S. Определите скорость снарядов после их взаимодействия. Сопротивлением трубы пренебречь.

11.5.21. Решите задачу 11.5.20 в случае, если масса первого снаряда m1, а второго m2, а скорость снарядов равна соответственно v1 и v2 (v1 > v2).

11.5.22 . Докажите, что сверхпроводящее кольцо индуктивности L, налетающее со скоростью v на соосное ему магнитное поле, отразится этим полем, если кинетическая энергия кольца будет меньше Φ2/2L, где Φ — максимальный поток магнитного поля через кольцо.

♦11.5.23 . Медное кольцо радиуса r и массы m висит на нити, совершая малые крутильные колебания с периодом T . Индуктивность кольца L. Как изменится период колебаний кольца, если его поместить в горизонтальное однородное магнитное поле индукции B, параллельное плоскости кольца в положении равновесия? Момент инерции кольца относительно оси, проходящей по диаметру, равен J. Сопротивлением кольца пренебречь.

♦11.5.24 . Сверхпроводящая коробка разделена на две равные части также сверхпроводящей перемычкой толщины d. Размеры коробки показаны на рисунке (h a, l). По коробке в направлении, перпендикулярном перемычке, циркулирует ток, линейная плотность которого i. С какой частотой будет колебаться перемычка, если ей сообщить небольшую скорость в направлении, показанном на рисунке? Масса перемычки m.

♦ 11.5.25 . Между двумя свехпроводящими шинами с постоянной скоростью v0 движется поршень по направлению к перемычке массы m, образуя сверхпроводящую цепь. Найдите максимальную скорость перемычки, если в начальный

237

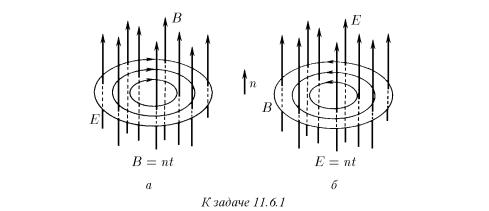
момент она покоилась, ток в цепи был равен I0, а расстояние между поршнем и перемычкой было равно x. Индуктивность на единицу длины шин L. Трением пренебречь.

11.5.26 . Внутри проводящей цилиндрической оболочки создано магнитное поле. Оболочке сообщается скорость v таким образом, что она начинает сжиматься к оси, не теряя симметрии. Найдите максимальную индукцию магнитного поля, которая может быть получена таким способом, если начальная индукция B0 = 10 Тл, v = 3 км/с, начальный радиус оболочки r0 = 20 см, ее толщина

= 0,5 см, плотность материала оболочки ρ = 8,9 г/см3. Найдите максимальное магнитное давление, действующее на оболочку. Электрическим сопротивлением оболочки пренебречь.

11.5.27 . Внешнее магнитное поле индукции B, в котором находится длинная идеально проводящая трубка, полностью стенками трубки не экранизируется из-за того, что масса электронов конечна. Поле частично проникает внутрь трубки. Ось трубки направлена вдоль магнитного поля, ее радиус r много больше толщины стенок h. Число электронов проводимости в единице объема материала трубки ne. Рассчитайте индукцию поля, проникшего внутрь трубки, в случае

B = 10 Тл, r = 1 мм, h = 0,1 мм, ne = 1020 см−3.

11.5.28 . Если длинный идеально проводящий тонкостенный цилиндр раскрутить вокруг своей оси, то внутри цилиндра возникает магнитное поле. Найдите его индукцию, если угловая скорость цилиндра ω.

§11.6. Связь переменного электрического поля

смагнитным

♦11.6.1. Согласно закону электромагнитной индукции переменное магнитное поле порождает вихревое электрическое поле. Точно так же переменное электрическое поле порождает вихревое магнитное поле, но при изменении электрического поля направление вектора B образует правый винт с направлением вектора dE/dt. Коэффициент же пропорциональности в СГС, связывающий эти поля, в обоих явлениях одинаков. Пользуясь этим свойством электромагнитного поля, определите в СГС и в СИ зависимость циркуляции индукции магнитного поля по замкнутому контуру от скорости изменения потока электрического смещения через этот контур.

♦ 11.6.2. а. Плоский конденсатор движется со скоростью v, как показано на рисунке. Напряженность электрического поля между пластинами E. Определите

238

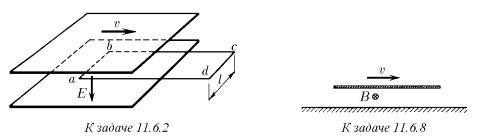
скорость изменения потока электрического поля через прямоугольный контур abcd и циркуляцию индукции магнитного поля по этому контуру. Как связаны друг с другом искомые величины в СИ? в СГС?

б. Приведите примеры, подтверждающие пропорциональность циркуляции индукции магнитного поля по контуру скорости изменения потока электрического поля через поверхность, ограниченную этим контуром.

11.6.3. Чему равен поток электрического смещения через площадь, ограниченную замкнутым контуром, если при равномерном убывании этого потока до нуля в течение 1 мкс в контуре возникает циркуляция индукции магнитного поля

0,001 Тл ·м?

11.6.4 . Магнитное поле при разряде конденсатора создается не только током в проводнике, но и изменяющимся электрическим полем в пространстве между обкладками конденсатора, причем изменяющееся электрическое поле создает такое магнитное поле, как если бы между обкладками существовал ток, равный току в проводнике. Докажите это.

11.6.5. Напряженность однородного электрического поля внутри плоского конденсатора с обкладками радиуса 10 см линейно растет со временем: E = αt, где α = 9 · 1010 В/(м ·с). Чему равна индукция магнитного поля внутри конденсатора на расстоянии 5 см от его оси?

11.6.6.В колебательном контуре возбудили свободные колебания. Во сколько раз максимальная индукция магнитного поля внутри плоского конденсатора меньше максимальной индукции магнитного поля в катушке индуктивности? Радиус пластин конденсатора r, расстояние между ними h, длина катушки L, число витков N.

11.6.7.Плоский конденсатор, напряженность электрического поля внутри которого E, движется со скоростью v. Скорость образует угол α с пластинами. Какова индукция магнитного поля внутри конденсатора?

♦ 11.6.8. При движении параллельно поверхности металла равномерно заряженной пластины со скоростью v возникает магнитное поле индукции B. Определите поверхностную плотность заряда пластины.

11.6.9. Внутри плоского конденсатора параллельно его обкладкам движется со скоростью v проводящая пластина, толщина которой равна половине расстояния между обкладками конденсатора. На обкладках конденсатора поддерживается напряжение V , расстояние между ними h.

а. Чему равна индукция магнитного поля внутри проводника? между движущимся проводником и обкладками конденсатора?

б. Как изменится индукция магнитного поля в пластине, если проводник заменить диэлектриком с диэлектрической проницаемостью ε?

11.6.10 . В неподвижной диэлектрической среде с диэлектрической проницаемостью ε движется параллельно своим пластинам плоский заряженный конденсатор. Как изменится индукция магнитного поля внутри конденсатора, если среда будет двигаться вместе с ним?

239

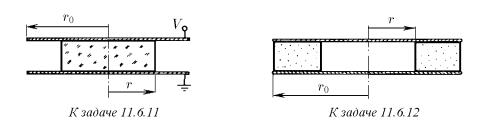
♦ 11.6.11 . а. Напряженность электрического поля внутри круглого плоского конденсатора, заполненного веществом с диэлектрической проницаемостью ε, линейно растет со временем: E = αt. Определите индукцию магнитного поля внутри конденсатора на расстоянии r от его центра.

б. Напряжение на обкладках плоского конденсатора линейно растет со временем: V = αt. Радиус обкладок r0, расстояние между ними h. По оси конденсатора вставлен диэлектрический цилиндр радиуса r с диэлектрической непроницаемостью ε. Определите индукцию магнитного поля на боковой поверхности цилиндра и на краю конденсатора.

♦ 11.6.12 . Плоский изолированный конденсатор, пластины которого — параллельные металлические круги радиуса r0, заполнен веществом, исключая центральную цилиндрическую область радиуса r. Конденсатор разряжается через это вещество. Ток разрядки равен I. Определите зависимость индукции магнитного поля внутри конденсатора от расстояния до оси конденсатора. Постройте график этой зависимости.

240