
PDF. Семестр 1. Ответы на вопросы к коллоквиуму по аналитической геометрии. Ярослав Ермилов (МП-14)
.pdf30.10.2015 |
Ярослав Ермилов (МП-14) |
9. Выражение смешанного произведения через координаты векторов (в косоугольной и в прямоугольной системе координат).
В косоугольной системе координат Если в косоугольной системе координат, с единичными (не обязательно)
векторами , и , три вектора заданы в координатном виде: = {1, 2, 3},
= { 1, 2, 3}, = { 1, 2, 3}, то их смешанное произведение имеет вид:
1 2 3
< , , > = | 1 |
2 |
3| < |
, , |
> |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
||
Доказательство: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
< , , > = < |
+ |
2 |
+ |
, |
|
+ |
+ , |
|
+ |
+ |
> = |
|||||
|
|
1 |
|
|
3 |
1 |
2 |
3 |
1 |
2 |
3 |
|
||||
= 1 1 1 < , , > + 1 1 2 < , , > + . . . |
+ 3 3 3 |
< , , > |
|
|||||||||||||
Нулевые элементы: < , , > = 0, |
< , , > = 0 и т.д. |
|
|
|||||||||||||
Выпишем ненулевые элементы: |
|
|
|
|
|
|
|
|
|
|
||||||
1 2 3 < , , > + 1 3 2 < , , > |
+ 2 1 3 < , , > + |
|
||||||||||||||
+ 2 3 1 < , , > + 3 1 2 < , , > |
+ 3 2 1 < , , > = |
|
||||||||||||||
= ( 1 2 3 − 1 3 2 − 2 1 3 + 2 3 1 + 3 1 2 − 3 2 1) < , , > = |
|
|||||||||||||||
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= | 1 |
2 |
3| < , , >, что и требовалось доказать |
|
|
|
|||||||||||
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
10. Уравнение плоскости. |
|
|
|
|
|
|
|
|
|
|
||||||
Общее уравнение плоскости |
|
|
|
|
|
|
|
|
|
|
||||||
Общее |
уравнение |
|
плоскости |
|
имеет |
|
вид |
+ + + = 0, |
где |
|||||||
коэффициенты , и С не равны нулю одновременно.
Нормальный вектор (вектор нормали) плоскости – это вектор, который
перпендикулярен данной плоскости. |
|
|
||||
Для плоскости, заданной уравнение вида + + + = 0: |
= { , , } |
|||||
Уравнение плоскости по точке и двум неколлинеарным векторам |
|
|
||||
Дано: |
точка |
0( 0, 0, 0) и два неколлинеарных вектора |
= { , , }, |
|||
= { |
, |
, }. |
Уравнение плоскости, которая проходит через |
точку |
||
|
|
|
|
|
|
0 |
параллельно векторам и (либо через них) имеет вид: |
|
|
||||
− |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
| − 0 |
|
| = 0 |
|
|
||
− |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
«Ответы на вопросы к коллоквиуму по аналитической геометрии» |
-11- |

30.10.2015 |
Ярослав Ермилов (МП-14) |
Примечание: Если вектора будут коллинеарными, то точка и два таких коллинеарных вектора не будут определять плоскость (векторы будут свободно «вертеться» вокруг точки).
Уравнение плоскости по трём точкам Если даны три (несовпадающие и не лежащие на одной прямой) точки, то
уравнение плоскости, проходящее через эти точки имеет вид:
( , , |
), |
( , , |
), ( , , ) |
|
0 0 0 |
1 1 1 1 |
2 2 2 2 |
||
− 0 |
1 − 0 |
2 − 0 |
||
| − 0 |
1 − 0 |
2 − 0| = 0 |
||
− 0 |
1 − 0 |
2 − 0 |
|
|
Примечание: данный способ определения плоскости является координатным представление предыдущего способа, где в качестве неколлинеарных векторов
|
|
выступают вектора 0 1 |
и 0 2. |
Уравнение плоскости по точек и нормальному вектору Уравнение плоскости, проходящей через точку 0( 0, 0, ) перпенди-
кулярно нормальному вектору = { , , } имеет вид:
( − 0) + ( − 0) + ( − 0) = 0
Примечание: если раскрыть скобки и объединить постоянные величины − ∙ 0, − ∙ 0 и − ∙ 0 в новую постоянную величину , то получится общее уравнение плоскости + + + = 0, где = − ∙ 0 − ∙ 0 − ∙ 0
11. Уравнение прямой в пространстве: каноническое, параметрическое.
|
|
|
|
|
|
|
|
|
|
|
{ , |
} – направляющий вектор прямой |
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(вектор, параллельный или совпадающий с прямой) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
Возьмём , тогда: |
|
|
|
|
|||
|
|
|
|
|
|
(; ; ) |
|
, т.к. 0 и |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
||||||
|
|
|
|
{ |
|
; |
; } |
|
|
|
|
|
|
|
{ − 0, − |
|||
|
|
|
|
|
|
|
|
|
|
Вектор |
|
координаты |
||||||
|
|
|
|
|
|
|
|
|
|
|
0 имеет |
|||||||
|
|
|
|
|
|
|
|
|
|
|
− , − }, |
∙ = { |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, }, приравняв |
||||||
|
|
|
( |
; |
|
, |
|
|
) |
|
0 |
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
− |
= |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
и∙ получим:{ − 0 = (1) и (2)
− 0 =
|
|
|
= |
+ |
|
|
|
|
|
|
||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
(1) |
{ |
= |
+ |
|
– параметрическое уравнение прямой |
|
||||||
|
0 |
|
|
|
|
|||||||
|
|
|
= |
+ |
|
|
|
|
|
|
||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(2) |
|
− 0 |
= |
− 0 |
= |
− 0 |
|
– каноническое уравнение прямой |
|
|||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
«Ответы на вопросы к коллоквиуму по аналитической геометрии» |
-12- |
|||||||||||
30.10.2015 Ярослав Ермилов (МП-14)
12. Уравнение прямой в п-мерном пространстве. Уравнение гиперплоскости.
Уравнение прямой в п-мерном пространстве |
|
|
|
|
|
||||||||||||||||||
|
Если |
= ( 0 |
, 0 |
, … , 0) |
– фиксированная точка прямой , = { , , … , |
|
} |
||||||||||||||||
|
|
|
|
0 |
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
– направляющий вектор прямой, то каноническое уравнение прямой имеет вид: |
|
|
|||||||||||||||||||||
− 0 |
|
− 0 |
|
|
|
|
− 0 |
|
|
|
|
|
|
|
|
|
|||||||
1 |
1 |
= |
|
2 |
|
2 |
=. . . = |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение гиперплоскости |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Гиперплоскость |
n-мерного |
|
пространства — подпространство |
|
с |
|||||||||||||||||
размерностью, на единицу меньшей, чем объемлющее пространство, т.е. n−1 |
|
|
|||||||||||||||||||||
|
Если |
= ( 0 |
, 0 |
, … , 0) |
– фикс. точка гиперплоскости, = ( , |
2 |
, … , |
|
) |
||||||||||||||
|
|
|
|
0 |
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
– нормальный вектор гиперплоскости, то уравнение гиперплоскости имеет вид: |
|
|
|||||||||||||||||||||
|
( − 0) + |
2 |
( − 0)+. . . + |
|
( − 0) = 0 |
|
|
|
|
||||||||||||||
1 |
1 |
1 |
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|||||
∙ + |
2 |
∙ +. . . + |
|
∙ + = 0 |
|
|
|
|
|
|
|
||||||||||||
1 |
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
13. Расстояние и отклонение точки от прямой на плоскости. |
|
|
|
|
|||||||||||||||||||
|
Если на плоскости задана точка ( |
|
, ) и прямая , заданная уравнением |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вида + + = 0, то расстояние и отклонение этой точки от прямой можно найти по следующим формулам:
|
| ∙ + ∙ + | |
|
∙ + ∙ + |
||||
( , ) = |
|
|
; ( , ) = |
|
|
||
√ |
|
|
√ |
|
|
||
|
2 + 2 |
|
|
2 + 2 |
|
||
Примечание: доказательство аналогично доказательству нахождения расстояния и отклонения точки от прямой в пространстве (
«Ответы на вопросы к коллоквиуму по аналитической геометрии» |
-13- |
30.10.2015 |
Ярослав Ермилов (МП-14) |
15. Расстояние и отклонение точки от плоскости.)
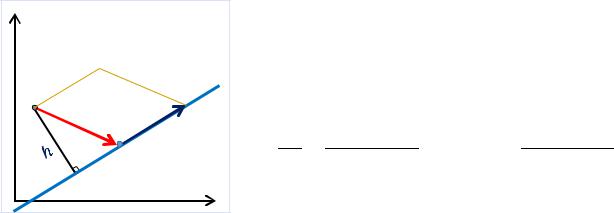
14. Расстояние от точки до прямой в пространстве. |
|
|||||
|
|
|
Пусть точка 0 |
принадлежит прямой , для |
||
|
|
которой задан направляющий вектор , тогда |
||||
|
|
|
|
|
|
, ) |
|
|
[ 0 |
× ] = | 0| ∙ | | ∙ sin( 0 |
|||
S |
|
|
|
|
|
|
|
|
= |[ 0, ]|; с другой стороны = ∙ | | |
||||
|
|
|
|
|
|
|
|
|
|
|[ 0 × ]| |
|[ 0 × ]| |
||
|
|
= |
| | = |
| | |
(, ) = |
| | |
|
|
|
|
|
|
|
«Ответы на вопросы к коллоквиуму по аналитической геометрии» |
-14- |

30.10.2015 |
|
|
|
|
|
|
|
Ярослав Ермилов (МП-14) |
||||
15. Расстояние и отклонение точки от плоскости. |
|
|
|
|
||||||||
Первый способ (через параметрический вид уравнения перпендикуляра): |
|
|
|
|||||||||
|
|
|
|
|
|
Дано: : + + + = 0; ( , , ) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Чтобы |
найти расстояние от точки |
|
до |
||||
|
|
|
|
|
||||||||
|
|
|
|
плоскости |
|
проведём |
прямую |
. |
||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
Направляющий вектор прямой совпадает с |
||||||
|
|
|
|
|
|
нормальным вектором плоскости α. Запишем |
||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
уравнение прямой в параметрическом виде: |
||||||
|
|
|
|
|
|
= |
+ ∙ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
+ ∙ |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
: { |
|
|
|
|
|
|
|
|
|
|
|
|
= |
+ ∙ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставим выраженные через параметр значения координат PK в |
||||||||||||
уравнение плоскости: |
|
|
|
|
|
|
|
|
|
|||
( + ∙ ) + ( + ∙ ) + ( |
+ ∙ ) + = 0 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
t ∙ (A2 + 2 + 2) = − ∙ − ∙ − ∙ − |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∙ + ∙ + ∙ + |
|
|
|
|
|
|
|
|||||
= − |
|
|
|
|
− значение параметра для точки К |
|
||||||
|
|
|
|
|
||||||||
|
|
2 + 2 + 2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
| ∙ + ∙ + ∙ + | ∙ √2 + 2 + 2 |
|
||||||
(, ) |
|
| | |
∙ | | = |
|
|
|
|
|
|
= |
||
= | | = |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
2 + 2 + 2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
| ∙ + ∙ + ∙ + | |
|
|
|
|
|
|
|||||
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
√2 + 2 + 2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||
|
| ∙ + ∙ + ∙ + | |
|
|
|
|
|
|
|||||
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
√2 + 2 + 2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||
|
∙ + ∙ + ∙ + |
|
|
|
|
|
|
|||||
(, ) |
= |
|
|
|
|
|
|
|
|
|
|
|
√2 + 2 + 2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||
Второй способ (через проекцию): |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
Дано: : + + + = 0; ( , , ) |
|||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Чтобы найти расстояние от точки до |
||||||
|
|
|
|
|
|
плоскости выберем произвольную точку 0 |
||||||
|
|
|
|
|
|
на плоскости и спроецируем вектор |
|
|||||
|
|
|
|
|
|
0 на |
||||||
|
|
|
|
|
|
нормальный |
вектор |
|
плоскости |
α. |
Длина |
|
|
|
|
|
|
полученной проекции вектора и есть |
|||||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
расстояние от точки до плоскости |
||||||
|
|
|
|
|
|
|
|
|
|
|||
(, ) |
|
|
| 0 |
| ∙ | | ∙ |
( 0 , ) |
|( 0 , )| |
||||||
= 0 = | 0 | ∙ ( 0 , ) = |
| | |
= |
|
| | |
||||||||
|
|
|
|
|
|
|
|
|
|
|||
«Ответы на вопросы к коллоквиуму по аналитической геометрии» |
|
-15- |
||||||||||
30.10.2015 |
|
|
|
|
|
|
Ярослав Ермилов (МП-14) |
|||
16. Расстояние между скрещивающимися прямыми. |
|
|
|
|||||||
|
|
|
|
Прямые 1 и 2 – скрещивающиеся, т.е. не |
||||||
|
|
лежат в одной плоскости, |
значит их можно |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
заключить в параллельные плоскости α и β. |
||||||
|
|
|
|
|
||||||
|
|
|
|
|
1 2 |
– общий перпендикуляр скрещива- |
||||
|
|
|
|
|
|
|||||
|
|
|
|
ющихся прямых 1 и 2. |
|
|
|
|||
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 2 , 1 2 , 1 2 1, Н1 2 2 |
||||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||
|
|
|
|
и |
– точки прямой |
и |
|
соответственно |
||
|
|
|
|
|
2 |
|||||
|
|
|
|
|
1 |
2 |
1 |
|
|
|
< , |
|
|
– |
объём параллелепипеда, построенного на векторах |
||||||
, 1 2 > = пар. |
||||||||||
, |
|
|
|
] = осн. – площадь его основания, 1 2 = – высота. |
||||||
и 1 2. [ × |
||||||||||
( |
, |
|
) = = пар. = |< |
|
, |
|
||||
|
|
, 1 2 >| |
||||||||
1 |
|
2 |
|
осн. |
|
|
|
|[ × ]| |
|
|
|
|
|
|
|
||||||
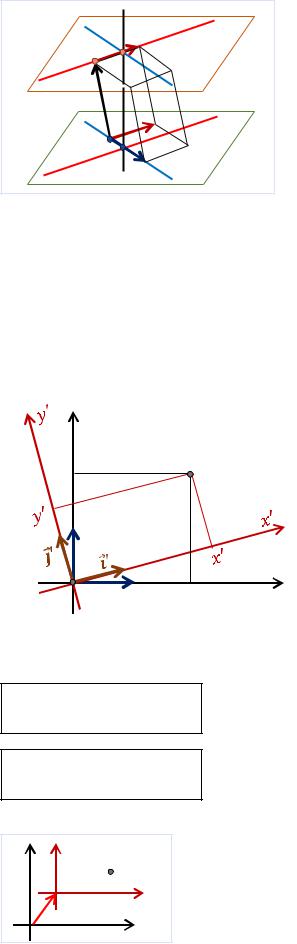
17. Параллельный перенос и поворот осей координат на плоскости.
Поворот системы координат относительно начала координат
|
|
|
|
Выразим координаты точки (, ) |
|||||
|
|
|
|
через систему координат ′ ′: (′, ′) |
|||||
|
|
|
|
|
|
|
′ |
||
|
|
|
|
|
|
|
|||
|
|
|
= ∙ + ∙ = ′ ∙ ′ + ′ ∙ |
|
|||||
|
|
|
|
= (cos , sin ) = ∙ cos + ∙ sin |
|||||
|
|
|
|
= (cos ( |
|
+ ) , sin ( |
|
+ )) = |
|
|
|
|
|
|
|||||
|
|
|
|
2 |
2 |
|
|
||
|
|
|
|
= ∙ − ∙ |
|||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
∙ + ∙ = ′( ∙ + ∙ ) + ′( ∙ − ∙ ) =
=( ′ ∙ cos − ′ ∙ sin ) + ( ′ ∙ + ′ ∙ cos )
′ = cos + sin { ′ = cos − sin
= ′ cos − ′ sin { = ′ cos + ′ sin
–формула перехода от старой системы к новой
–формула перехода от новой системы к старой
Параллельный перенос системы координат
|
′ |
|
’ = (, ), = (, ) = (′, ′) |
|||||||
|
′ |
|||||||||
|
′ |
{ |
′ |
= − |
{ |
= ′ + |
||||
|
|
|
′ |
= − |
= |
′ |
+ |
|||
|
|
|
|
|
|
|
||||
«Ответы на вопросы к коллоквиуму по аналитической геометрии» |
-16- |
30.10.2015 Ярослав Ермилов (МП-14)
18. Вывод канонического уравнения а) эллипса, б)гиперболы, в) параболы.
|
Эллипс. Определение. Каноническое уравнение. |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
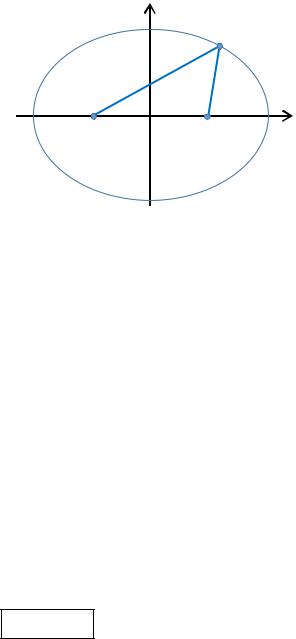
Эллипс – геометрическое место точек плоскости, для которых сумма |
||||||||||||||||
|
расстояний до двух фиксированных точек 1 и 2 |
этой плоскости, называемых |
||||||||||||||||||
|
фокусами, есть величина постоянная. |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если точка с координатами (, ) |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
(; ) |
|
– точка эллипса, то | 1| + | 2| = 2, |
|
|||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
т.е. 1 + 2 = 2, т.к. сумма двух сторон |
|
|||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
1 и 2треугольника 1 2 больше |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
(− ; ) |
(; ) |
|
|
третьей стороны F1 2 = 2, то 2 > 2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= √( + )2 |
+ 2, = √( − )2 + 2 |
, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
√( + )2 + 2 + √( − )2 + 2 = 2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
+ |
|
2 |
= 1 |
– каноническое уравнение эллипса |
|
|
|
|
|
|
|
||||||
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Гипербола. Определение. Каноническое уравнение.
Гипербола – геометрическое место точек плоскости, для которой абсолют-
ная величина разности расстояний до двух фиксированных точек 1 и 2 этой
плоскости, называемых фокусами, есть величина постоянная.
|
2 |
− |
2 |
= 1 |
– каноническое уравнение гиперболы |
|
2 |
2 |
|||
|
|
|
|
Парабола. Определение. Каноническое уравнение.
Парабола – геометрическое место точек плоскости, для которых расстояние до некоторой фиксированной точки этой плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой этой плоскости,
называемой директрисой.
2 = 2 – каноническое уравнение параболы
19. Общее уравнение кривой 2-го порядка. Избавление от “ ” с помощью
поворота.
|
2 + 2 |
+ |
22 |
2 + 2 |
+ 2 |
23 |
+ |
33 |
= 0 |
– уравнение |
кривой |
|||
11 |
12 |
|
13 |
|
|
|
|
|
|
|
|
|||
второго порядка в общем виде, где |
2 + 2 |
+ |
22 |
2 – квадратичная часть, |
||||||||||
|
|
|
|
|
11 |
|
|
12 |
|
|
|
|
|
|
213 + 223 – линейная часть, 33 – свободный член. |
|
|
||||||||||||
«Ответы на вопросы к коллоквиуму по аналитической геометрии» |
-17- |
|||||||||||||
30.10.2015 |
|
Ярослав Ермилов (МП-14) |
= ′ cos − ′ sin |
′ = cos + sin |
|
{ = ′ cos + ′ sin |
{ ′ = cos − sin |
– формулы перехода к новой, |
повёрнутой на угол , системе координат ’ ’:
11 2 + 212 + 22 2+ . . . = 011(′ − ′ )2 + 212( ′ − ′ )( ′ + ′ ) +
+ 22( ′ + ′ )2+ . . . = 0
|
Коэффициент перед = 0, т.е. |
|
|
|
|
|
|
|
|
|
|
|
||||||||
−2 |
|
∙ ∙ + 2 ( 2 |
− 2 ) |
+ 2 |
22 |
∙ ∙ = 0 |
||||||||||||||
11 |
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
−11 sin 2 + 212 cos 2 + 22 2 = 0 |
|
|
|
|
|
|
|
|
|
|||||||||||
( 22 |
− 11) sin 2 = −212 cos 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
tg 2 = − |
|
212 |
; 2 = |
212 |
|
; = |
|
1 |
|
212 |
|
|
||||||||
|
22 |
− |
|
|
− |
22 |
2 |
|
− |
22 |
|
|||||||||
|
|
|
|
11 |
11 |
|
|
|
|
|
|
|
11 |
|
|
|||||
Вывод: чтобы избавиться от нужно повернуть систему координат на угол ,
который равен |
1 |
|
|
2 12 |
|
2 |
|
11 |
− |
||
|
|
|
|
22 |
|
20. Приведение к каноническому виду уравнения кривой 2-го порядка. Классификация кривых 2-го порядка.
21. Построение и свойства эллипсоида.
22. Построение конуса и гиперболоидов. Асимптотический конус гиперболоида.
23. Построение параболоидов.
24. Цилиндрические поверхности. Цилиндры второго порядка.
25. Приведение к каноническому виду уравнения поверхности 2-го порядка:
а) , , ≠ ; б) , ≠ , = ; в) ≠ , , = ; Классификация
поверхностей 2-го порядка.
«Ответы на вопросы к коллоквиуму по аналитической геометрии» |
-18- |
