
PDF. Семестр 1. Ответы на вопросы к коллоквиуму по аналитической геометрии. Ярослав Ермилов (МП-14)
.pdf30.10.2015 |
Ярослав Ермилов (МП-14) |
Ответы на вопросы к коллоквиуму по аналитической геометрии
1. Определители 2-го и 3-го порядков и их свойства.
Определитель 2-го порядка Пусть заданы числа 1, 2, 1 и 2 (действительные или комплексные), тогда
число 1 2 − 2 1 |
называется определителем 2-го порядка: |
||||||
(1) | 1 |
2| = − |
2 |
|
||||
1 |
2 |
1 |
2 |
|
|
1 |
|
|
|
|
|
|
|
||
Определителем |
2-го |
порядка называется число, полученное из элементов |
|||||
матрицы 2 на 2, путём вычитания из произведения элементов, стоящих на главной диагонали, произведения элементов, стоящих на побочной диагонали.
Числа 1, 2, 1 и 2 в определителе (1) называются элементами определителя. В определителе (1) также различают первую строку (1, 2),
вторую строку (1, 2), первый столбец (1, 1) и второй столбец (2, 2).
Определитель 3-го порядка Определителем 3-го порядка называется число определяемое с помощью
элементов матрицы 3 на 3 следующим образом: |
|
|
|
|
|
|
|
|
|
|||||||||||||
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) | 1 |
2 |
3 |
| = + |
3 |
+ |
2 |
− |
3 |
− |
− |
||||||||||||
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
|
1 |
3 |
1 |
2 |
|
1 |
2 |
3 |
1 |
2 |
3 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Аналогично, числа |
1, |
2, |
3, 1, |
|
2, |
3, |
1, |
2, |
3 |
в |
определителе (2) |
|||||||||||
называются элементами определителя. В определителе (2) также различают
первую, вторую и третью строки, а также первый, второй и третий столбцы.
Свойства определителей 2-го и 3-го порядка:
1) Свойство равноправности строк и столбцов
▪Если строки матрицы определителя сделать столбцами с теми же номерами (т.е. транспонировать матрицу), то определитель не изменится.
▪Другими словами: при транспортировке матрицы определитель не меняется.
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
| 1 |
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
| = | |
2 |
|
| |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
Доказательство: |
|
|
|
|
|
|
|
|
|
|
|
||||
(1) | |
1 |
2 |
| = |
− |
|
(2) | |
|
|
| = |
− |
|
||||
1 |
2 |
1 |
1 |
||||||||||||
|
|
|
1 2 |
|
2 1 |
|
|
2 |
|
1 2 |
|
2 1 |
|||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
(1) = (2) свойство верно, что и требовалось доказать
«Ответы на вопросы к коллоквиуму по аналитической геометрии» |
-1- |
30.10.2015 |
Ярослав Ермилов (МП-14) |
2)Свойство антисимметрии при перестановке двух строк (столбцов)
▪Если переставить местами две строки (столбца), то определитель изменит знак на противоположный.
▪Другими словами: при перестановке двух строк или столбцов определитель меняет знак на противоположный.
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
| = − | a |
2 |
| |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
Доказательство: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
| 1 |
2 |
| = |
− |
|
|
(1) |
|
|
|
|
|
|
|
|
|
||
1 |
2 |
1 |
2 |
|
2 |
1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
− | 1 |
2| = −( |
2 |
− |
) = − |
2 |
+ |
= |
− (2) |
|||||||||
1 |
2 |
|
1 |
|
|
2 |
1 |
1 |
2 |
1 |
1 |
2 |
2 |
1 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(1) = (2) свойство верно, что и требовалось доказать
3)Линейное свойство определителя
▪Если каждый элемент некоторой строки (столбца) представить в виде суммы двух слагаемых, то определитель будет равен сумме двух определителей, у которых все строки (столбцы) кроме данной строки (столбца) прежние, а в данной строке (столбце) ы первом определителе стоят первые слагаемые, а во втором определителе – вторые.
4)▪Если все элементы строки (столбца) умножить на одно и то же число, то и определитель умножится на это число.
▪Другими словами: при умножении всех элементов строки или столбца на число определитель тоже умножается на это число.
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
| 1 |
2 |
| = | 1 |
|
2| |
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
Доказательство: |
|
|
|
|
|
|
|
|
|
|
||
| 1 |
2| = |
− |
2 |
|
= ( |
− |
2 |
) (1) |
||||
1 |
2 |
1 |
2 |
|
|
1 |
1 |
2 |
|
1 |
||
|
|
|
|
|
|
|
|
|
|
|
||
| 1 |
2| = ( |
− |
2 |
) |
(2) |
|
|
|
|
|||
1 |
2 |
1 |
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(1) = (2) свойство верно, что и требовалось доказать |
||||||||||||
5) Если элементы какой либо строки (столбца) равны нулю, то и определитель
равен нулю. |
|
|
| |
0 0 | = 0 ∙ − 0 ∙ = 0 |
|
|
2 |
1 |
|
1 2 |
|
6) Если соответствующие элементы двух строк (столбцов) равны, то определитель
равен нулю. |
|
|
|
|
|
|
|
| 1 |
2| = |
2 |
− |
2 |
= 0 |
|
|
1 |
2 |
1 |
|
1 |
|
||
|
|
|
|
|
|
||
«Ответы на вопросы к коллоквиуму по аналитической геометрии» |
-2- |
||||||
30.10.2015 |
Ярослав Ермилов (МП-14) |
7)Если соответствующие элементы двух строк (столбцов) пропорциональны, то определитель равен нулю.
8)Если к каждому элементу одной из строк (столбцов) прибавить соответ- ствующие элементы другой строки (столбца), умноженные на число, то определитель не изменится.
9)Свойство алгебраических дополнений соседних строк (столбцов)
▪Сумма произведений элементов какой-либо строки (столбца) определителя на соответствующие алгебраические дополнения элементов любой другой строки (столбца) равна нулю
2. Скалярное произведение векторов и его свойства.
Скалярным произведением двух ненулевых векторов и называют число, равное произведению длин этих векторов на косинус угла между ними.
Обозначение: , ∙ , (, ).
Определение: ∙ = | | ∙ | | ∙ cos(, )
Так как | | ∙ cos(, ) = и | | ∙ cos(, ) = , то получаем, что
∙ = | | ∙ = | | ∙ , т.е. скалярное произведение двух векторов равно произведению модуля одного из них и проекции другого на ось, сонаправленную с первым вектором.
^ ,
Скалярное произведение векторов через координаты:
Скалярным произведением двух ненулевых векторов и на плоскости или в трёхмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов и . То есть для векторов ( , ), ( , ) справедливо следующее:
|
∙ = | |
| ∙ | | ∙ (, ) = |
|
|
+ |
|
|
|
|
|
|
|
|
|
|
||
«Ответы на вопросы к коллоквиуму по аналитической геометрии» |
-3- |
|||||||
30.10.2015 Ярослав Ермилов (МП-14)
Доказательство:
Отложим от начала системы координат (точки O) следующие векторы:
|
= { |
, |
} |
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= |
= = { , }, тогда |
= − = − . |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рассмотрим треугольник . По теореме косинусов: |
|
|
|
|
|
|||||||||||||||||||||||
2 = 2 + 2 |
− 2 ∙ ∙ ∙ cos( , ) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
| − |2 |
= | |2 + | |2 |
− 2 ∙ | | ∙ | | ∙ (, ) |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
| − |2 |
= | |2 |
+ | |2 |
− 2 ∙ ∙ |
|
∙ = 1/2 (| |2 + | |2 |
− | − |2) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
∙ = 1/2 ((√ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
)2) ) = |
|||||||||
+ 2) |
+ (√ 2 + 2) − (√( |
− |
|
)2 + ( |
|
− |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= 1/2 (2 |
+ 2 |
+ 2 |
+ 2 |
− ( |
|
− |
)2 − ( |
− |
|
)2) = |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= 1/2 (2 |
+ 2 |
+ 2 |
+ 2 |
− 2 |
+ 2 |
|
− 2 |
− 2 |
+ 2 |
|
− 2)= |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= 1/2 (2 |
|
+ 2 |
|
) = |
|
+ |
|
, что и требовалось доказать. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
− = { − , − }
= { , }
= { , }
Свойства скалярного произведения векторов:
1)∙ = ∙ – переместительный закон скалярного произведения (комму-
тативность)
Доказательство:
∙ = | | ∙ | | ∙ (, )
∙ = | | ∙ | | ∙ ( , )| т. к. | | ∙ | | = | | ∙ | | и (, ) = ( , ),
то ∙ = ∙ , что и требовалось доказать
«Ответы на вопросы к коллоквиуму по аналитической геометрии» |
-4- |

30.10.2015 |
Ярослав Ермилов (МП-14) |
2)( ∙ ) ∙ = ( ∙ ) – однородность по первому ( ∙ ( ∙ ) = ( ∙ ) – по второму) множителю (ассоциативность)
Доказательство: через координаты: ∙ { , }, { , } ( ∙ ) ∙ = + = ( + ) = ( ∙ )
3) ( + ) = ∙ + ∙ – распределительный закон скалярного произведения
(дистрибутивность)
Доказательство:
▪ через координаты: { , }, { , }, { , }( + ) = { ( + ), ( + )} = { + , + } (1)
∙ + ∙ = { , } + { , } = { + , + } (2) (1) = (2) свойство верно, что и требовалось доказать
▪ через проекции:
( + ) = | | ∙ ( + ) = | | ∙ ( + ) = | | ∙ + | | ∙ = = ∙ + ∙
4) 2 = | |2 – скалярный квадрат вектора равен квадрату его длины
Доказательство:
2 = ∙ = | | ∙ | | ∙ (, ) = | | ∙ | | ∙ 1 = | |2
3. Вычисление с помощью скалярного произведения | |, , (, ).
Определение скалярного определения описано в 2. Скалярное произведение векторов и его свойства..
∙ = | | ∙ | | ∙ cos(, )
|
|
| | = |
|
|
|
∙ |
|
|
|
||
|
|
|
| | ∙ (, ) |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(, ) = |
|
∙ |
|
|
|||||
|
|
| | ∙ | | |
|
||||||||
|
|
|
|
|
|
|
|
||||
∙ = | | ∙ |
= | | ∙ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∙ |
| | ∙ |
|
|||
|
|
|
= |
|
|
= |
|
|
|
||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
| | |
|
|
| | |
|
|
|
|
|
|
|
|
|
|
|
|||
«Ответы на вопросы к коллоквиуму по аналитической геометрии» |
-5- |
30.10.2015 |
|
|
|
|
|
|
|
|
|
|
Ярослав Ермилов (МП-14) |
|||
4. Уравнения прямой на плоскости: общее, каноническое, параметрическое. |
|
|||||||||||||
Общее уравнение прямой |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
{, } |
– |
нормальный |
вектор |
прямой |
|
|||
|
|
|
|
|
(любой |
ненулевой |
вектор, |
перпендикулярный |
||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
данной |
прямой), где |
и |
не равны нулю |
||||||
( ; ) |
|
|
|
|||||||||||
|
(; ) |
одновременно. |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
M0(0, 0) – точка, принадлежащая прямой |
|
|||||||
|
|
|
|
|
|
(, ) – произвольная точка |
|
|
|
|||||
|
|
( ; |
) |
|
Возьмём , тогда: |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, т.к. 0 и |
|
|
|
||||||
|
|
|
|
|
|
0 |
|
|
|
|||||
|
|
|
|
|
|
|
∙ |
= 0,т.к. |
|
|
|
|
||
|
|
|
|
|
|
0 |
cos( 0, ) = 0 |
|
|
|||||
Вектор |
|
имеет |
координаты |
{ − 0, − 0}. |
Запишем |
скалярное |
||||||||
0 |
||||||||||||||
произведение векторов |
|
|
|
|
|
|
|
|
|
|
||||
и 0 в координатном виде: |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∙ 0 = ( − 0) + ( − 0) = 0; |
|
|
|
|
|
|
|
|||||||
+ 0 + + 0 = 0; 0 + 0 |
= |
|
|
|
|
|
||||||||
+ + = 0 |
– общее уравнение прямой |
|
|
|
|
|
||||||||
Частные случаи: |
|
|
|
|
|
|
|
|
|
|
|
|
||
1)≠ 0, ≠ 0, = 0 – прямая проходит через начало координат
2)= 0, ≠ 0, ≠ 0 – прямая параллельна оси
3)≠ 0, = 0, ≠ 0 – прямая параллельна оси
4)= 0, ≠ 0, = 0 – прямая совпадает с осью
5)≠ 0, = 0, = 0 – прямая совпадает с осью
Уравнение прямой с угловым коэффициентом
= – коэффициент наклона прямой
− 0 = ( − 0) – уравнение прямой с угловым коэффициентом
«Ответы на вопросы к коллоквиуму по аналитической геометрии» |
-6- |
30.10.2015 |
|
|
|
|
|
|
|
|
|
|
|
|
Ярослав Ермилов (МП-14) |
||||
Каноническое и параметрическое уравнения прямой |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
{ |
, } |
– направляющий вектор прямой |
|||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
( |
|
; ) |
|
(вектор, параллельный или совпадающий с прямой) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(; ) |
|
Возьмём , тогда: 0 , т.к. 0 и |
||||||||
|
|
|
|
|
|
|
|
|
|
имеет координаты |
{ − 0, − 0}, |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
Вектор 0 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
∙ = { |
|
, |
|
и ∙ получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
}, приравняв |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
− = |
|
|
||||
|
|
|
( ; ) |
|
|
{ |
0 |
|
|
|
(1) и (2) |
|
|||||
|
|
|
|
|
− = |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
+ |
|
|
|
|
|
|
|
|
|
|
|||
(1) |
|
0 |
|
|
|
|
– параметрическое уравнение прямой |
|
|||||||||
|
|
{ = |
+ |
|
|
||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
(2) |
|
|
− 0 |
= |
|
− 0 |
|
– каноническое уравнение прямой |
|
||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5. Векторное произведение векторов и его свойства. |
|
||||||||||||||||
|
|
Векторным произведением вектора |
на вектор называется вектор такой |
||||||||||||||
что, он перпендикулярен векторам и , его длина равна | | = | | ∙ | | ∙ (, ), и направлен он так, что тройка векторов является правой тройкой.
Обозначение: [ ], [, ], ×
Определение: [, ] = , , , | | = | | ∙ | | ∙ (, ) , − пр. тр.
Геометрические свойства векторного произведения:
1)Если векторное произведение двух векторов равно нулю, то эти векторы коллинеарны (т.е. лежат на параллельных прямых или на одной прямой).
2)Модуль векторного произведения двух векторов равен площади параллелограмма, образованного этими векторами
Алгебраические свойства векторного произведения:
1)[, ] = −[ , ] – антикоммутативность
Доказательство:
[ , ] |
= ′, |
′ , |
′ , |
| ′| = | | ∙ | | ∙ (, ) , |
′ − пр. тр. |
′ , |
| ′| |
= | |, |
= −′ |
|
|
«Ответы на вопросы к коллоквиуму по аналитической геометрии» |
-7- |
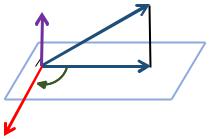
30.10.2015 |
Ярослав Ермилов (МП-14) |
2)[ , ] = [, ] – сочетательное свойство (ассоциативность) Доказательство:
а) λ > 0
|
[, ] = , |
, |
|
, | | = | | ∙ | | ∙ (, ) , |
− пр. тр. |
|
|
|
|||||||||||||||||||
|
[ |
|
|
|
′ |
, |
′ |
|
( ) |
′ |
, |
|
′ |
|
|
′ |
↑↑, |
′ − пр. тр. |
|
|
|
||||||
|
, ] = |
|
|
|
|
|
|
| |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
| ′| = | | ∙ | | ∙ ( , ) = ∙ |
| | ∙ | | ∙ ( , ) | ′| = ∙ | | |
|
|
|||||||||||||||||||||||
|
′ = ∙ |
[ , ] = [, ], что и требовалось доказать |
|
|
|
||||||||||||||||||||||
|
б) λ = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
[ , ] = , |
[, ] = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
что и требовалось доказать |
|
|
|
|
|||||||||||||
|
= [ , ] = [, ], |
|
|
|
|
||||||||||||||||||||||
|
в) λ < 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
аналогично пункту а) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
[( + ), ] = |
[, ] + [ , ] – распределительное свойство (дистрибутивность) |
||||||||||||||||||||||||||
|
Лемма: ′′ = [, ], где – единичный вектор, | | = 1, |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ = , |
′′ |
| ′| = | | ∙ (, ′), |
– |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
вектор |
|
′, повёрнутый |
в |
плоскости γ |
на |
90°, |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
значит | ′′| = | ′| |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
′′ , ′′ |
, | ′′| = | | ∙ | | ∙ (, ), |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
° |
|
|
|
|
|
|
|
|
|
т.к. (, ′) = (, ), |
| | ∙ (, ) |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
′′ |
|
|
|
|
|
|
|
|
|
|
|
′′ – правая тройка |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Значит ′′ = [, ], что и требовалось доказать |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Доказательство: |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Пусть = λ ∙ , где |
– единичный вектор, т.е. | | = 1, тогда |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′′ |
|
′ |
′ |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
||||||||
[( + ), ] = [( + ), λ ∙ ] = λ [( + ), ] = λ ( + ) |
= (( + ) ) |
|
|||||||||||||||||||||||||
=λ (′′ + ′′) = λ ∙ ′′ + λ ∙ ′′ = λ [, ] + λ [ , ] = [, ∙ ] + [ , ∙ ] =
=[, ] + [ , ], что и требовалось доказать
4)[, ] =
Доказательство:
[, ] = , | | = | | ∙ | | ∙ (, ) = , т. к. (, )
«Ответы на вопросы к коллоквиуму по аналитической геометрии» |
-8- |
30.10.2015 |
Ярослав Ермилов (МП-14) |
6. Выражение векторного произведения через координаты векторов.
Если векторы заданы в координатном виде: = { , , }, = { , , }, то их векторное произведение имеет вид:
[ , ] = { − , − , − }, т.е.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
[ , ] = | |
|
|
|
| |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство: |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
∙ + |
∙ + |
|
|
|
|
∙ + |
|
|
|||
[ , ] = [( |
|
∙ ), ( ∙ + |
∙ )] = . . . = |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ( − ) ∙ + ( − |
|
|
|
|
|
|
|
||||||||
|
) ∙ + ( − ) ∙ = |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= | |
|
| ∙ − | |
|
| ∙ + | |
|
|
| ∙ |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Примечание: расписать, пользуясь свойствами |
векторного произведения, а так |
||||||||||||||
же тем, что для базиса |
|
|
|
|
|
|
|
|
|
||||||
, , : |
|
|
|
|
|
|
|
|
|||||||
[ , ] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= , [ , ] = , [ , ] = , |
|
|
|
|
|
|
|
||||||||
[ , ] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= , [ , ] = , [ , ] = , |
|
|
|
|
|
|
|
||||||||
[ , ] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= − , [ , ] = − , [ , ] = − |
|
|
|
|
|
||||||||||
7. Двойное векторное произведение. |
|
|
|
|
|||||||||||
[ , [ , ]] = ( |
∙ ) − ( ∙ ) – формула Лагранжа |
|
|
||||||||||||
Доказательство: |
|
|
|
|
|
|
|
|
|
|
|
||||
Повернём систему координат так, чтобы вектор был сонаправлен с осью OX, а вектор лежал в плоскости XOY, т.е.
= { 1, 0, 0}, = { 1, 2, 0}, = { 1, 2, 3}
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
∙ 2 |
− 2 ∙ 1) |
(1) [ , ] = | |
0 | = ( 2 ∙ 3) − ( 1 ∙ 3) + ( 1 |
||||||
1 |
2 |
|
|
|
|
|
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
[ , [ , ]] = | |
|
|
|
|
|
||
|
|
0 |
0 |
| = |
|
|
|
|
1 |
|
|
|
|
|
|
|
2 ∙ 3 |
− 1 ∙ 3 |
1 ∙ 2 − 2 ∙ 1 |
|
|
|
|
=∙ 0 − ∙ 1( 1 ∙ 2 − 2 ∙ 1) + ∙ 1(− 1 ∙ 3) =
={0, 1 ∙ 2 ∙ 1 − 1 ∙ 1 ∙ 2, − 1 ∙ 1 ∙ 3}
(2) ( ∙ ) − ( ∙ ) = { 1, 2, 0} ∙ ({ 1, 0, 0} ∙ { 1, 2, 3}) − −{ 1, 2, 3} ∙ ({ 1, 0, 0} ∙ { 1, 2, 0}) =
«Ответы на вопросы к коллоквиуму по аналитической геометрии» |
-9- |
30.10.2015 |
Ярослав Ермилов (МП-14) |
={ 1, 2, 0} ∙ 1 ∙ 1 − { 1, 2, 3} ∙ 1 ∙ 1 =
={ 1 ∙ 1 ∙ 1, 1 ∙ 2 ∙ 1, 0} − { 1 ∙ 1 ∙ 1, 1 ∙ 1 ∙ 2, 1 ∙ 1 ∙ 3} =
={0, 1 ∙ 2 ∙ 1 − 1 ∙ 1 ∙ 2, −1 ∙ 1 ∙ 3}
(1)= (2) [, [ , ]] = ( ∙ ) − ( ∙ ), что и требовалось доказать
Примечание: векторное произведение векторов не зависит от системы координат.
8. Смешанное произведение векторов. Его геометрический смысл и свойства.
Смешанным произведением трёх векторов называют число, полученное путём скалярного умножения векторного произведения [, ] векторов и , на вектор , т.е. < , , > = ([, ], )
Обозначение: < , , >
Определение: < , , > = ([, ], )
Геометрические свойства:
1)Смешанное произведение векторов , и равно объёму параллелепипеду,
построенному на этих векторах, приведённых к общему началу, взятому со знаком «+», если тройка правая, и со знаком «–», если тройка левая
2)Если смешанное произведение векторов , и равно нулю, то эти векторы компланарны (лежат в одной плоскости)
Алгебраические свойства:
1)< , , >=< , , > =< , , > – циклический сдвиг
2)< , , >= −< , , > – антикоммутативность
3)< + , , >=< , , > + < , , > – дистрибутивность по 1-му элементу
4)< ∙ , , > = < , , > – ассоциативность по 1-му элементу Примечание: доказывать, раскрывая по определению, применяя свойства скалярного и векторного произведений.
«Ответы на вопросы к коллоквиуму по аналитической геометрии» |
-10- |
