
3. Законы больших чисел и предельные теоремы теории вероятностей.
3.1. Законы больших чисел.
Ряд утверждений и теорем в теории вероятностей объединены общим названием: законы больших чисел.
Эти законы делятся на две группы. К первой группе относятся утверждения, касающиеся оценок вероятностей больших отклонений случайной величины Х от ее математического ожидания, справедливые для любого распределения. Суть этой группы законов можно выразить краткой формулой: большие отклонения от mX мало вероятны. Ко второй группе законов относятся утверждения о сходимости некоторых последовательностей случайных величин (теорема Чебышева и ее обобщения).
Неравенства Чебышева.
Первое неравенство Чебышева.
Пусть Х – случайная величина с конечным mX
![]() (3.1.1)
(3.1.1)
![]() Пусть,
для определенности, Х-СВНТ.
Запишем
по определению математическое ожидание
от модуля случайной величины X
:
Пусть,
для определенности, Х-СВНТ.
Запишем
по определению математическое ожидание
от модуля случайной величины X
:
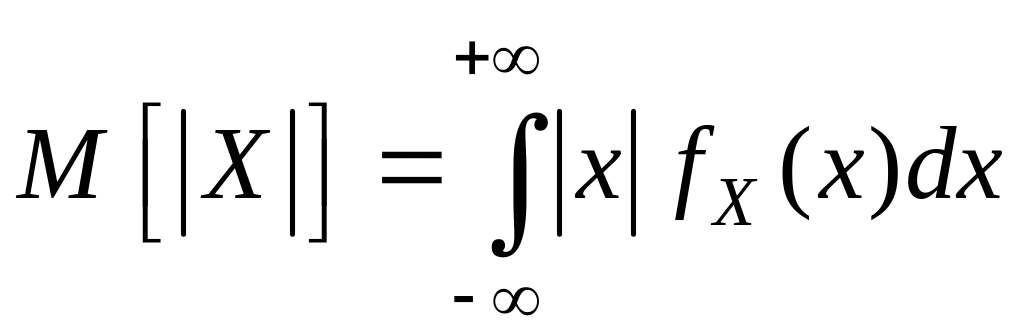
Выберем произвольное >0, разобьем маршрут интегрирования на два непересекающиеся интервала и воспользуемся свойством аддитивности интеграла по области.

В силу неотрицательности подинтегральной функции получаем
![]() ,
,
откуда
следует (3.1.1).
![]()
Следствие.
Пусть Х
![]() 0
по одному из свойств математического
ожидания
mX
0
уравнение (3.1.1) перепишется в виде:
0
по одному из свойств математического
ожидания
mX
0
уравнение (3.1.1) перепишется в виде:
![]() (3.1.2)
(3.1.2)
Второе неравенство Чебышева (в центрированной форме).
Пусть
случайная величина Х
имеет
конечные mX
и
![]()
![]() (3.1.3)
(3.1.3)
Обозначим,
как и ранее в главе 2,
![]() -центрированная
случайная величина. Учитывая очевидное
равенство
-центрированная
случайная величина. Учитывая очевидное
равенство

и применяя доказанное выше первое неравенство Чебышева (3.1.1), получим:
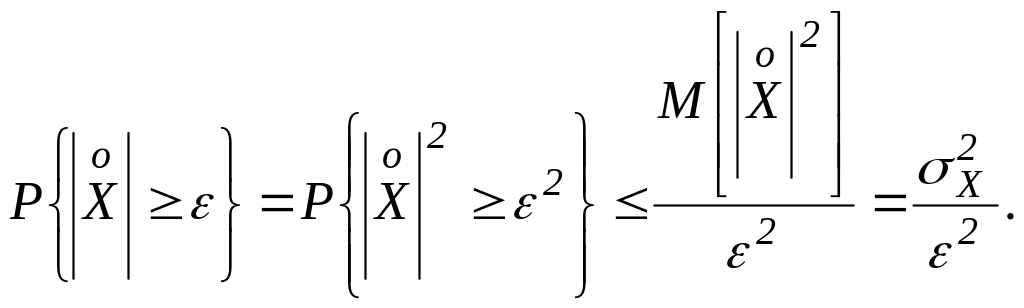
что и требовалось доказать.►
Пример 3.1.1. Пусть X-число бракованных изделий из 100 наудачу отобранных из большой партии, поступившей в продажу. За большой период посчитано, что в среднем для этого вида изделий брак составляет 1%. Оценить вероятность события {X 5 }.
Т.к.
Х>0
и по условию mX=0,01100=1,то
по следствию из первого неравенства
Чебышева
P{X
5}
![]()
![]()
Пример
3.1.2.
Пусть в условиях примера (3.1.1) известно,
что
![]() .Оценить
P{X
5}.
.Оценить
P{X
5}.
Заметим, что в силу условия X>0,
P{X
5}
P{|X-1|
4}

![]()
Заметим, что вероятность существенно уменьшилась!
Пример
3.1.3
Предположим, X~PU(=1),
что
хорошо согласуется с данными задачи
(одним из признаков этого является
равенство: mX=
)
и
соответствует закону редких явлений.
Оценим снова вероятность события
![]() .
.
P{X
5}=![]() Это
более, чем в 17 раз меньше предыдущей
оценки!
Это
более, чем в 17 раз меньше предыдущей
оценки!
Пример 3.1.4. В условиях примера 3.1.2. оценить вероятность события {X 2}.
◄ Очевидно,
что в силу условия
![]() имеем следующую цепочку отношений между
событиями
имеем следующую цепочку отношений между
событиями
![]() . (3.1.4)
. (3.1.4)
Действительно,
![]()
откуда и следует (3.1.4).
Отсюда по закону поглощения получаем
![]() ,
,
т.е. получили тривиальный результат ►
Сделаем
некоторые выводы. Последние примеры
показывают, что чебышевские оценки
сверху
вероятностей
больших отклонений случайной величины
X
от ее
математического ожидания являются
довольно грубыми, что является платой
за незнание закона распределения сл.вел.
X.
На практике неравенства Чебышева имеет
смысл применять при условии
![]() .
Однако теоретическое значение неравенств
(3.1.1) – (3.1.3) большое, что будет ясно из
дальнейшего.
.
Однако теоретическое значение неравенств
(3.1.1) – (3.1.3) большое, что будет ясно из
дальнейшего.
Еще раз отметим, что рассмотренные выше примеры касались оценок сверху больших отклонений. Для получения оценок снизу следует перейти в неравенствах (3.1.1) – (3.1.3) к противоположным событиям. Например из (3.1.3) получаем:
![]() (3.1.5)
(3.1.5)
Пример 3.1.5 Средняя длина детали, производимой на конвейерной линии, равна 50 см, а дисперсия 0,1 см2. Оценить снизу вероятность того, что длина случайно взятой детали окажется в интервале (49,5; 50,5).
◄ Пусть
X
–длина случайно взятой детали. Очевидно,
что события
![]() и
и
![]() равносильны. Поэтому, согласно неравенству
(3.1.5) P
1–
равносильны. Поэтому, согласно неравенству
(3.1.5) P
1–![]() ►
►
Пример 3.1.6. В условиях предыдущего примера оценить снизу вероятность события {49<X<52}.
◄ Очевидно,
что {49<X<52}
![]() {48<X<52}=
{48<X<52}=![]() .
Поэтому по свойству вероятности
.
Поэтому по свойству вероятности
![]() .
►
.
►
Пример 3.1.7. Случайная величина X дискретного типа задана законом распределения
|
0,3 |
0,6 |
|
0,2 |
0,8 |
а)
Используя неравенство Чебышева, оценить
снизу вероятность события {![]() }.
}.
б) Найти точное значение вероятности указанного события.
◄ а)
Находим дисперсию:
![]() 0,09*0,2+0,36*0,8-0,542=0,0144.
0,09*0,2+0,36*0,8-0,542=0,0144.
Далее, согласно неравенству (3.1.5), получаем:
P{
}
1–![]() 1–0,36=0,64.
1–0,36=0,64.
б) Используем закон распределения и цепочку очевидных равенств
P{ }=P{0,34<X<0,74}=P{X=0,6}=0,8. ►
Пример 3.1.8. Устройство состоит из 10 независимо работающих элементов. Вероятность отказа каждого элемента за время t равна 0,03.
а)
Оценить вероятность события
![]() ,
используя неравенство Чебышева.
,
используя неравенство Чебышева.
б) Найти точное значение указанной вероятности.
◄ а)
Согласно постановке эксперимента
![]() ,
где n=10,
p=0,03.
Поэтому
,
где n=10,
p=0,03.
Поэтому
![]() =0,5;
=0,5;
![]() =
=![]() =0,5*0,93.
Далее используя (3.1.5), получаем
=0,5*0,93.
Далее используя (3.1.5), получаем
![]() =0,88123.
=0,88123.
б) Для точного ответа на вопрос используем биномиальный закон и формулу Бернулли:
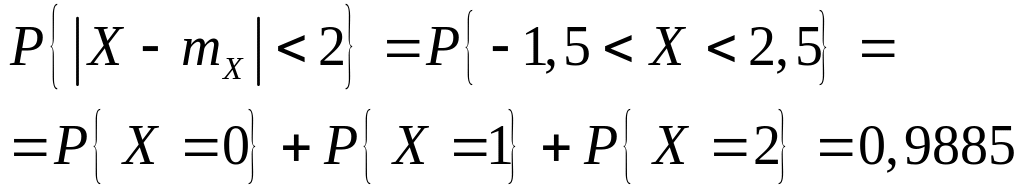
Пример 3.1.9. Игральная кость подбрасывается 6 раз. Пусть X – число выпадений четной цифры.
а)
Оценить по Чебышеву вероятность события
![]() .
.
б) Найти точное значение указанной вероятности.
◄ а)
По условию эксперимента
![]() ,
где n=6,
p=0.3.
Отсюда следует:
,
где n=6,
p=0.3.
Отсюда следует:
![]() ,
,
![]() =1,3.
Далее согласно неравенству (3.1.3):
=1,3.
Далее согласно неравенству (3.1.3):
![]()
![]() .
.
б) Используем закон распределения:
![]() =2
=2![]() (1/2)6=1/32.
►
(1/2)6=1/32.
►![]()
Анализируя результаты последних трех примеров обнаруживаем следующую закономерность: оценки по Чебышеву сверху всегда завышены по сравнению с точными значениями вероятности, в то время как оценки снизу – занижены.
Упражнения.
3.1.7. Средний срок службы автомобильной свечи зажигания 4 года. Оценить снизу вероятность того, что данная свеча прослужит не более 8 лет.
3.1.8. Среднее значение расхода воды в некотором малом населенном пункте составляет 50000 л. в день. Оценить снизу вероятность того, что в этом населенном пункте расход воды в предновогодний день не превысит 120000 л.
3.1.9. В сентябре в среднем наблюдается 7 дождливых дней. Оценить вероятность того, что в сентябре 2007г. число дождливых дней будет больше 10.
3.1.10.
Пусть к данным задачи (3.1.7) добавлена
информация, что
![]() =0,5
года. Оценить ту же вероятность.
=0,5
года. Оценить ту же вероятность.
3.1.11.*
Неотрицательные случайные величины X
и Y
независимы, причем mX=6,
mY=4,
=1,5,
![]() =2.
Оценить снизу вероятности событий:
=2.
Оценить снизу вероятности событий:
![]() ,
,
![]() .
.
