Ответы к упражнениям

3.1.7. 0,3.

3.1.8. 0,583.

3.1.9. 0,727.

3.1.10. 0,984.

3.1.11. , . Указание. Использовать линейность оператора математического ожидания. Для вычисления использовать свойство оператора дисперсии (формула (), гл.2).

Задание для самостоятельной работы

[1] 18.542 – 18.548

Понятие сходимости по вероятности.

Определение. Последовательность случайных величин сходится к случайной величине Х по вероятности при n , если

( ) (3.1.6)

Достаточное условие сходимости по вероятности:

Здесь { } – зависящая от неотрицательная неслучайная последовательность.

Замечание 1. В частных случаях в качестве предельной величины может выступать и не случайная величина (например M[X]).

Замечание 2. Для сходимости по вероятности принято краткое обозначение

.

Замечание 3. Сходимость по вероятности принципиально отличается от обычного понятия сходимости неслучайных последовательностей.

Пример 3.1.10. Рассмотрим следующую последовательность случайных величин , где закон распределения Х_n описывается таблицей.

	0

a) Показать, что

б) Можно ли утверждать, что последовательность реализаций данной случайной последовательности сходится к 0 в обычном смысле?

а) В силу неотрицательности имеем следующую цепочку равенств:

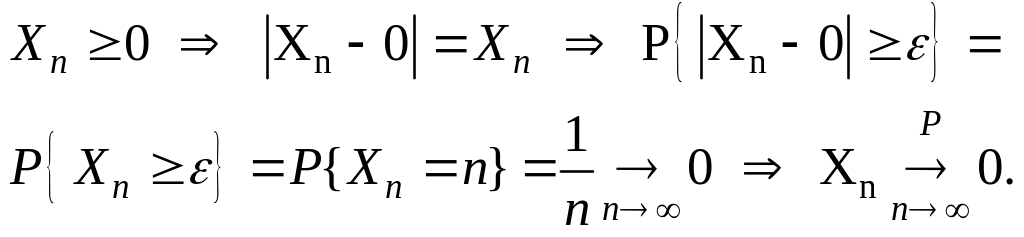
Таким образом, утверждение в пункте а) доказано.

б) Пусть эксперимент проведен и реализовалась последовательность x₁, x₂,…, x_n, где каждое x_n  {0,n}  на n-ом месте этой последовательности при может оказаться число n (поскольку вероятность этого события ненулевая)  ни одна из сколь угодно малых окрестностей точки x=0 не может считаться "ловушкой" для последовательности {x_n}.Таким образом, нельзя считать, что последовательность реализаций сходится к нулю в обычном смысле.

Пусть {X_n} – последовательность случайных величин с конечными математическими ожиданиями и дисперсиями. Для любого nN построим последовательность среднеарифметических ,  получим последовательность Y₁,Y₂…Y_n.,…

Определение. Говорят, что к последовательности {X_n} применим закон больших чисел, если

Теорема 3.1.1 (закон больших чисел в формулировке Чебышева).

Пусть для последовательности {X_n} выполняются следующие условия:

1. Элементы последовательности попарно независимы;

2. =0.

Тогда для {X_n} выполняется закон больших чисел.

Согласно второму неравенству Чебышева в центрированной форме:

Вычислим дисперсию среднего арифметического:

=

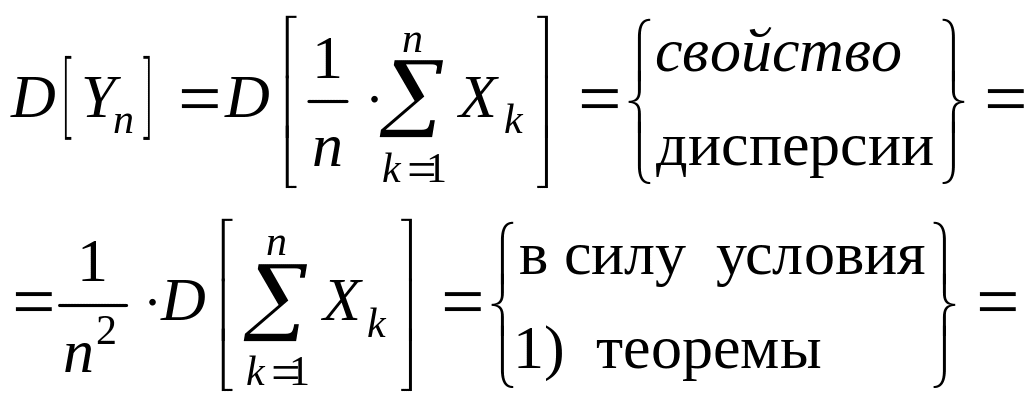
что следует из условия 2) теоремы.

Используем достаточное условие сходимости по вероятности:

Замечание 1. Теорема Чебышева остается верной, если заменить попарную независимость на попарную некоррелированность.

Замечание 2. Условие некоррелированности так же можно снять, но тогда придется вводить более жесткие условия для дисперсии (см. теорему Маркова в [3]).

Замечание 3. Имеют место следующие частные случаи проявления закона больших чисел:

1) то есть дисперсии членов последовательности равномерно ограничены  условие 2) выполняется;

2) все X_k попарно независимы, одинаково распределены и имеют конечную дисперсию

В последнем случае закон больших чисел формулируется следующим образом: “среднее арифметическое первых n членов последовательности сходится по вероятности к их общему мат.ожиданию”. В краткой записи:

Действительно,

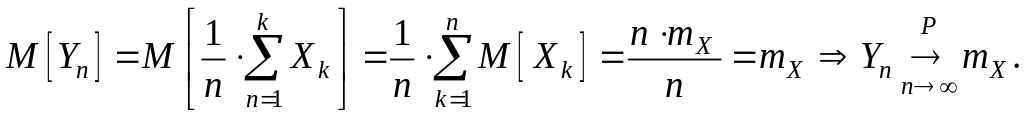
Теорема 3.1.2. (Закон больших чисел в формулировке Бернулли.

Пусть X_n - число успехов в n опытах по схеме Бернулли с вероятностью успеха в одном опыте, равным p (в краткой записи:X_n~B(n,p)). Обозначим -относительная частота успехов. Тогда справедливо следующее утверждение:

При увеличении числа опытов по схеме Бернулли относительная частота успехов сходится по вероятности к вероятности успеха в одном опыте.

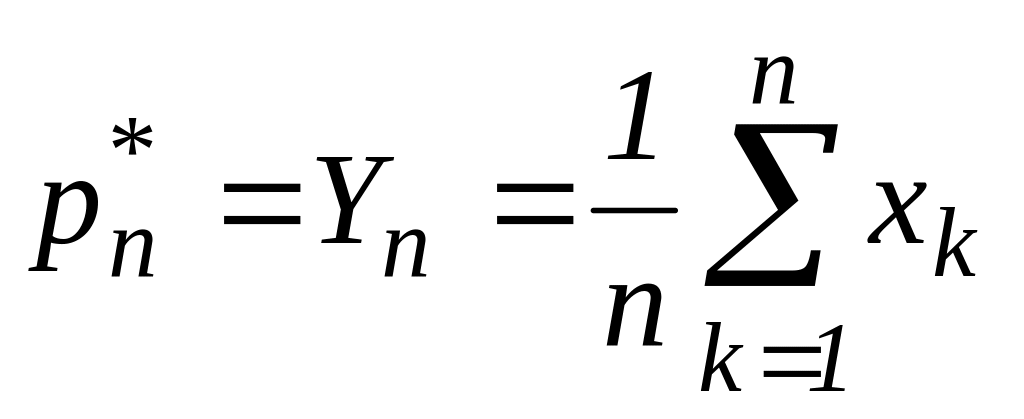
Обозначим I_k – индикатор успеха в k-ом опыте. Очевидно, что I_k~B(1,P), kN. При любом n элементы последовательности I₁,I₂…I_n – независимы в совокупности, а потому и попарно независимы. Условие 1) теоремы Чебышева выполняется. Кроме того: M[I_k]=p, D[I_k]=pq,  выполняется частный случай 2) теоремы Чебышева 

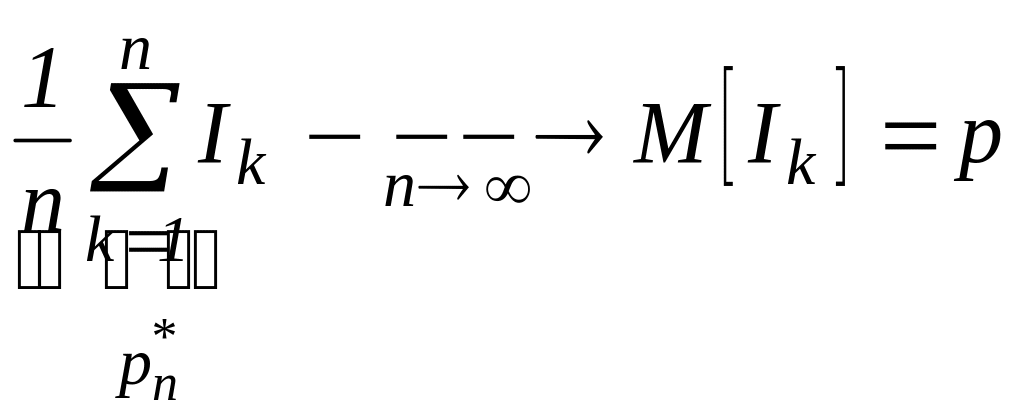
Теорема Бернулли играет большую роль в математической статистике, составляя основу для оценивания неизвестной вероятности событий в реальных экспериментах.

Пример 3.1.11. Случайная двоичная последовательность, вырабатываемая на ЭВМ, делится на группы из одинаковых символов (нулей и единиц). Обозначим - число знаков в i-ой группе; - среднее число знаков в серии, вычисленное по n сериям. Доказать, что последовательность сходится по вероятности к 2.

◄ Из условия следует, что последовательность - независимые случайные величины одинаково распределенные по закону Гео(p=0,5). Как было показано в главе 2, для геометрического распределения

= =2; = .

Таким образом, удовлетворяются условия частной теоремы Чебышева (случай 2)) Отсюда следует, что

=2, что и требовалось доказать ►

Пример 3.1.12. В последовательности случайные величины попарно независимы и распределены по закону . Применим ли к этой последовательности закон больших чисел?

◄ Используя известные характеристики равномерного распределения, получаем: =0, = . Проверим второе условие теоремы Чебышева:

.

Таким образом, условие 2) не выполняется и данная последовательность не подчиняется закону больших чисел.►

Пример 3.1.13. (сборка точных механизмов). Пусть - случайная длина детали, сходящей с конвейера. Известны ее основные характеристики:

=10 см, = =0,04 см²

Относительную точность изготовления детали можно характеризовать отношением . Производится сборка 9 подобных деталей (т.е. их длины складываются). Обозначим . Вычислить относительную точность для Y, т.е. отношение .

◄ Считая, что длина каждой изготовленной детали не зависит от остальных и используя свойства операторов матожидания и дисперсии, получаем:

.

Отсюда следует: = . Таким образом, относительная точность собранной детали повысилась в 3 раза. ►

Из рассмотренных примеров можно сделать следующий вывод: проявление закона больших чисел связано главным образом с тем, что сумма конечного числа независимых случайных слагаемых имеет меньший относительный разброс, измеряемый отношением С.К.О. к математическому ожиданию, чем у отдельно взятого слагаемого.