3.2 Центральная предельная теорема и ее применения.

Теорема 3.2.1 (Центральная предельная теорема в формулировке. Ляпунова) Пусть для последовательности случайных величин выполняются условия:

1)при любых n случайные величины - независимы в совокупности;

2)одинаково распределены;

3)существует , .

Обозначим: , , где .

Тогда

Замечание 1. Мы дали одну из простейших формулировок центральной предельной теоремы. Все более поздние формулировки связаны с устранением пункта 2), но тогда усложняется условие 3). Чаще всего оно формулируется в виде условия Линдеберга (гарантирует, что все слагаемые вносят равномерно малый вклад в общую дисперсию).[3]

Замечание 2. Из утверждения теоремы согласно свойству 7 характеристической функции следует, что предельным законом для при будет нормальный .

Центральная предельная теорема играет большую роль в приложениях теории вероятностей. Одним из ярких примеров применения этой теоремы на практике является баллистика, изучающая явления рассеивания снарядов при стрельбе по цели.

На траекторию полета снаряда действует множество независимых факторов: колебания атмосферного давления, влажности, температуры, отклонения величины заряда и веса снаряда от номинала, ошибка прицеливания, сила ветра на различных высотах и т.д. Результатом этих многочисленных воздействий, каждое из которых вносит свой равномерно малый вклад в общую сумму (ограниченность дисперсий!) является то, что отклонение точки попадания от цели удивительно точно описывается двумерным нормальным законом распределения.

Другим примером применения центральной предельной теоремы является теория и практика измерений. Всякое измерение неизбежно сопряжено с погрешностями. Реально наблюдаемая погрешность измерения является суммой элементарных погрешностей, вызванных многочисленными факторами, каждый из которых лишь незначительно влияет на результат. В силу центральной предельной теоремы результирующая погрешность должна быть приближенно нормальной. Это обстоятельство играет решающую роль в разработке эффективных методов обработки опытных данных в математической статистике.

Пример 3.2.1. Пусть - последовательность независимых одинаково распределенных случайных величин с конечными дисперсиями, , . Вычислить , если

а) .

б) .

в) .

◄ а) Пусть >0, , 1,2,…Преобразуем неравенство под знаком :

.

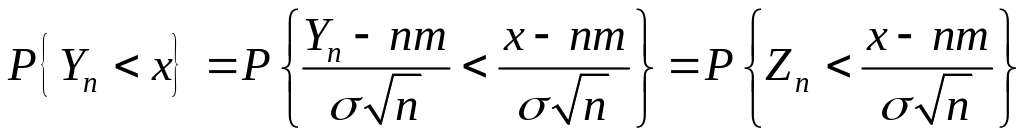Поскольку при , а предельным законом для при является нормальный, то получаем: =0.►

б) Ответ: =1.

в) Ответ: =0,3.

Пример 3.2.2. Пусть - последовательность независимых одинаково распределенных случайных величин с конечными дисперсиями, . Доказать, что .

Указание: преобразовать неравенство под знаком к неравенству со случайной величиной и воспользоваться результатом ЦПТ.

Пример 3.2.3. Пусть - последовательность независимых одинаково распределенных случайных величин с нулевыми математическими ожиданиями и конечными дисперсиями, . Найти , если известно, что

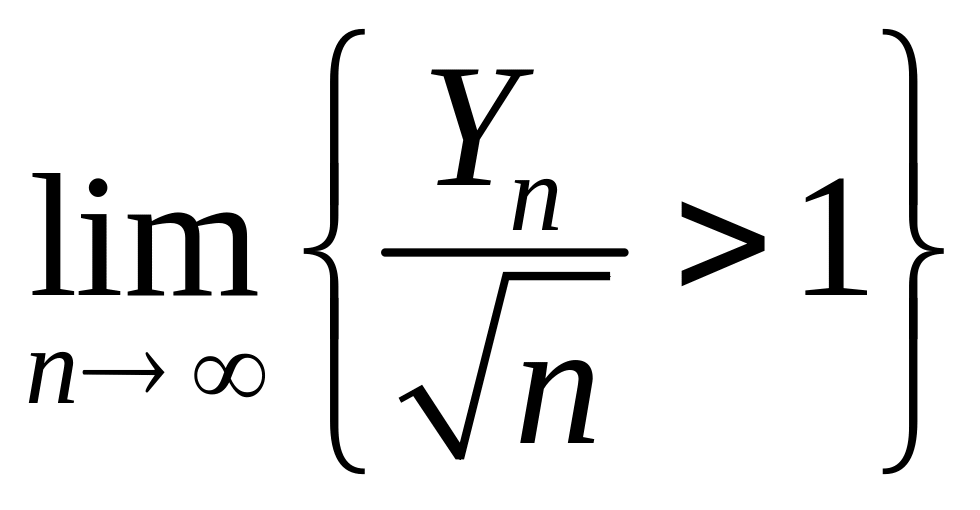=1/3.

Ответ: 2,23.

3.3. Предельные теоремы в схеме Бернулли.

Одним из важных для практики следствий центральной предельной теоремы является так называемая асимптотическая нормальность некоторых известных распределений. В частности, для биномиального распределения указанное свойство было доказано независимо А.Муавром (1730г.) и П.Лапласом (1812) задолго до появления ЦПТ и составило содержание двух теорем: так называемой локальной и интегральной теорем Муавра-Лапласа. Сформулируем их.

Теорема 3.3.1.( локальная теорема). Пусть - число успехов в n опытах по схеме Бернулли, p - вероятность успеха в одном опыте, - фиксированная величина. Тогда для достаточно больших n справедлива приближенная формула:

/ , (3.3.1)

где , а - плотность нормального стандартизованного распределения.

◄ Доказательство основано на применении формулы Стирлинга для факториалов в формуле Бернулли и вычислении предела при . Ввиду громоздкости вычислений мы этого доказательства не приводим (см., например, [3]).►

Теорема 3.3.2 (интегральная теорема Муавра-Лапласа). Пусть снова - число успехов в n опытах по схеме Бернулли, p - вероятность успеха в одном опыте. Тогда при условии для вероятности попадания случайной величины на промежуток справедлива приближенная формула:

, (3.3.2)

где - интеграл вероятности (функция нормального стандартизованного распределения).

◄ Доказательство, данное Муавром и Лапласом опирается на локальную теорему и здесь не приводится (см.например, [3] ).►

Покажем, что интегральная теорема является простым следствием центральной предельной теоремы. Действительно, поскольку по условию ~B(n, p), то можно использовать представление 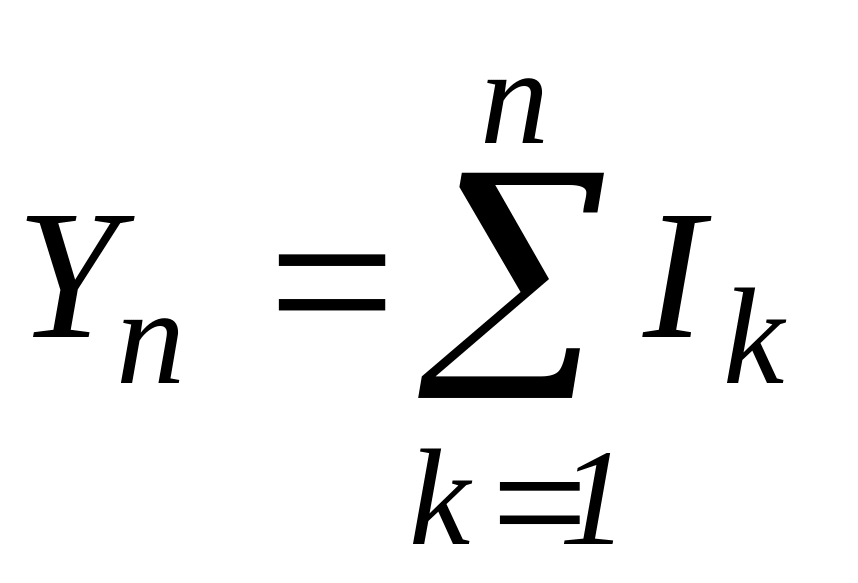, где I_k ~B(1, p) – индикатор успеха в k-м опыте по схеме Бернулли.Не трудно убедиться, что последовательность I₁ ,I₂ ,…, удовлетворяет всем условиям ЦПТ (см. ход доказательства теоремы 3.1.2.). 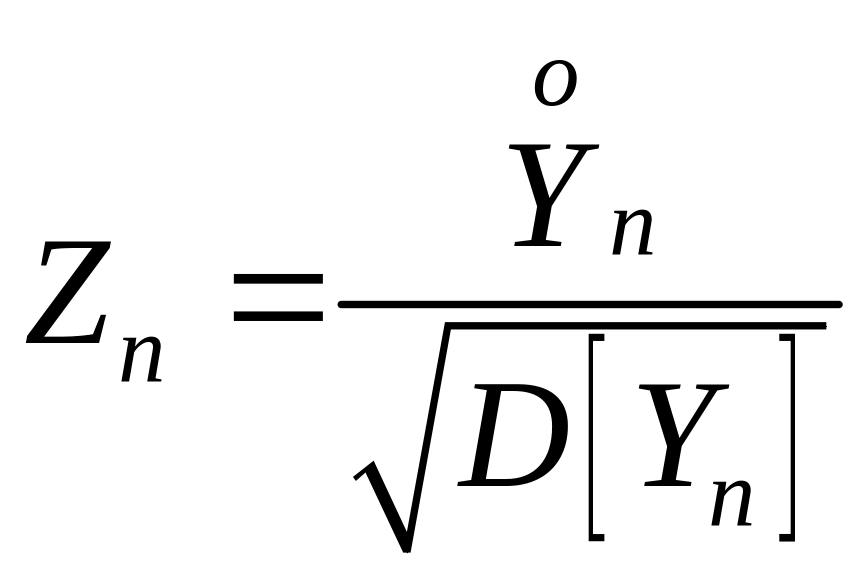Поэтому для стандартизованной случайной величины справедливо утверждение теоремы о предельном нормальном законе распределения. Отсюда, учитывая очевидное равенство

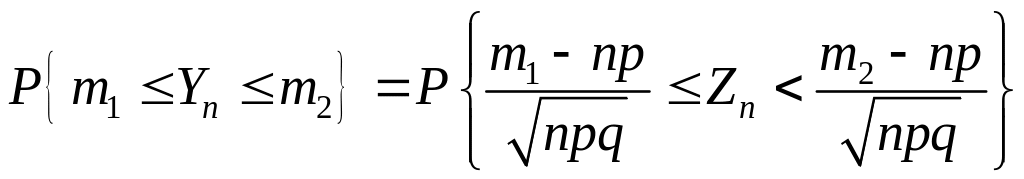, получаем формулу (3.3.2).

Пример 3.3.1. 100 раз подброшена правильная монета. Применяя локальную или интегральную теоремы Муавра-Лапласа, вычислить приближенно вероятность того, что герб выпадет а) ровно 50 раз; б) ровно 35 раз; в) от 45 до 65 раз.

◄ Пусть -число выпадений герба при 100 подбрасываниях монеты. Очевидно, что . Далее находим: 50, 3.

а) 0. По формуле (3.3.1), используя таблицу значений функции (плотности нормального стандартизованного распределения), находим:

=0,39894 5=0,0798.

б) -3. Аналогично предыдущему, находим: 0,00089.

в) По формуле (3.3.2), используя таблицу интеграла вероятности и свойства функции , находим:

0,9763.►

Пример 3.3.2 Компьютерная программа выдала 10000 случайных чисел из множества . Найти приближенное значение того, что число “нулей” будет заключено между 940 и 1060.

◄ По условию, числа 0,1,…,9, вырабатываемые генератором, имеют дискретное равномерное распределение с вероятностью реализации каждого числа 0,1. Обозначим число нулей, появившихся в 10000 испытаниях по схеме Бернулли. Очевидно, что . При этом 10000; 30. Используем интегральную теорему Муавра-Лапласа. По формуле (3.3.2) получаем:

0,93.►

Пример 3.3.3. Найти такое натуральное число , чтобы с вероятностью, не меньшей 0,9, можно было утверждать, что число мальчиков среди 900 новорожденных будет больше (считать рождение мальчика и девочки равновероятными и независимыми событиями).

◄ Обозначим - число мальчиков из 900 новорожденных. По условию можно считать, что . Искомое число должно удовлетворять неравенству

. Считая возможным нормальное приближение согласно интегральной теореме Муавра-Лапласа, по формуле (3.3.2) получаем:

, что равносильно неравенству .

Так как значение вероятности в правой части меньше 0,5, то аргумент функции отрицателен. Используя свойство интеграла вероятности, из последнего неравенства находим: , откуда окончательно следует: .►

Пример 3.3.4. После открытия Менделем законов наследственности многие ботаники проводили опыты по скрещиванию желтого (гибридного) гороха с зеленым. По известной гипотезе Менделя вероятность появления зеленого гороха в таких опытах должна быть равна . Проведя 34153 опыта, в 8436 случаях получили зеленый горох. Обозначим - относительная частота появления зеленого гороха. Ответить на следующие вопросы:

1) Вычислить вероятность события .

2) Вычислить вероятность того, что при повторении такого же числа 34153 опытов отклонение относительной частоты от 0,25 не превзойдет величины, полученной ботаниками.

◄ 1) По определению относительной частоты = , где - число успехов (число появлений зеленого гороха) в 34153 опытах по схеме Бернулли с вероятностью успеха в одном опыте 0,23. Отсюда получаем: =34153 0,25=8538,25; ; .

Далее используем формулу (3.3.2):

=0,7993.

2) В опытах получено значение относительной частоты 8436/34153=0,247, что соответствует величине отклонения от вероятности, равной 0,003,

=0,7995►

Пример 3.3.5. (продолжение). Сколько надо произвести опытов, чтобы с вероятностью не меньшей 0,99 можно было утверждать, что отклонение относительной частоты от 0,25 не превзойдет 0,01?

◄ Вопрос сводится к решению неравенства

относительно n. Используя характеристики и из предыдущего примера, преобразуем неравенство под знаком :

.

Применяя к последнему неравенству интегральную теорему Муавра-Лапласа, получаем: , откуда следует 0,993.

Далее с помощью таблицы квантилей нормального распределения находим: 80 2,576, откуда следует: ►

При качественной оценке условий применимости приближенных формул (3.3.1) и (3.3.2) необходимо оценить величину остаточных членов при замене биномиальных вероятностей на значения, получаемые с помощью формулы Стирлинга при конечном значении . Точную величину абсолютной погрешности получить в этом случае довольно сложно, но основной вывод заключается в том, что погрешность составляет величину порядка . Таким образом, для хорошего приближения нормальным законом условия недостаточно. Нужно, чтобы 1, что при больших и значениях или близких к 0 или 1, может не выполняться.

Основные рекомендации по практическому использованию формул (3.3.1) и (3.3.2) для инженерных расчетов вкратце сводятся к следующему. При значениях 0,5 хорошие приближения, дающие относительную погрешность в пределах 5% – 7%, получаются уже при 10. При этом, чем ближе значения (в формуле (3.3.1)) и (в формуле (3.3.2)) к значению , тем точнее получается результат.

Пример 3.3.6. 10 раз подброшена правильная монета. Вычислить вероятность того, что выпадет ровно гербов ( =0,1,…,10).

◄ Обозначим 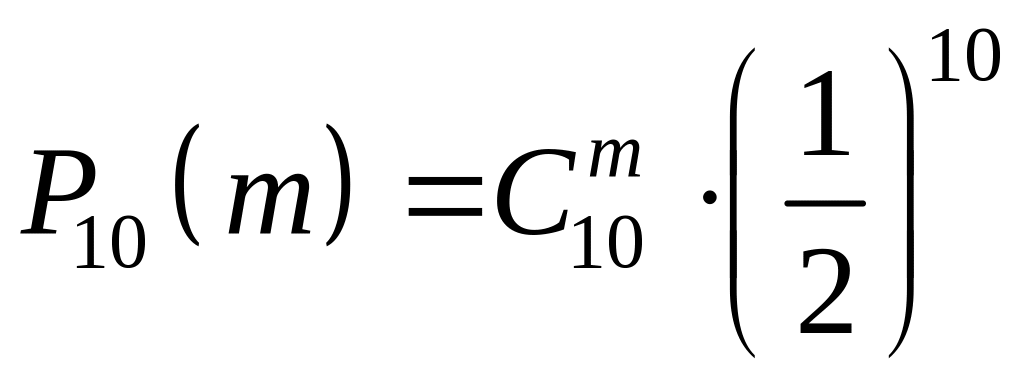- точные значения биномиальных вероятностей; - приближенные значения, определяемые по формуле (3.3.1).

В данном случае имеем: =5; = =1,5811; ;

= . Значения функции находим из таблицы П2 задачника [1]. Результаты вычислений приведены в таблице 3.3.1.

Отсутствующие в таблице значения вероятностей для восстанавливаются по уже найденным благодаря свойству симметрии биномиального распределения и четности функции : .

Таким образом, мы видим, что наихудший по точности результат получается при =0 и =10. При остальных значениях относительная погрешность приближения по локальной теореме Муавра-Лапласа не превышает 6% и дает наилучший результат при =4. ►

Таблица 3.3.1. (∆ - абсолютная погрешность, δ – относительная погрешность в %)

			∆	δ
0	0,00098	0,00171	0,00073	74,5%
1	0,00977	0,01028	0,00051	5,22%
2	0,04395	0,04150	0,00245	5,57%
3	0,11719	0,11408	0,00311	2,65%
4	0,20508	0,20690	0,00182	0,89%
5	0,24609	0,25231	0,00622	2,53%

При небольших значениях точность приближения по интегральной теореме Муавра-Лапласа можно значительно повысить, воспользовавшись так называемой поправкой Феллера в формуле (3.3.2) [] :

(3.3.3)

При этом следует иметь в виду, что точность приближений (3.3.2) и (3.3.3) зависит не только от величины , но и от промежутка .

Пример 3.3.7. Сделано 100 независимых выстрелов по цели с вероятностью попадания =0,23. Пусть - число попаданий при 100 выстрелах. Вычислить вероятности для трех промежутков: [15,35], [20,30] и [30,40].

◄ Обозначим = 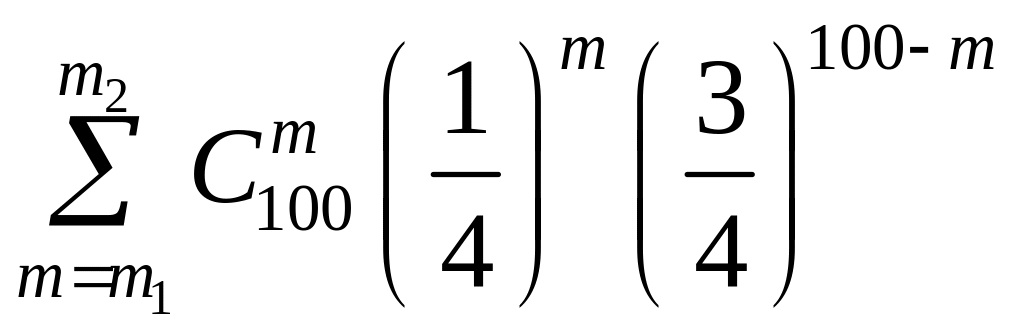- точное значение искомой вероятности по формуле Бернулли; - нормальное приближение, вычисленное по формуле (3.3.2); - уточненное по Феллеру приближение по формуле (3.3.3). Результаты вычислений с точностью до 4-х знаков после запятой приведены в таблице 3.3.2

Таблица 3.3.2 ( - относ.погрешность приближения , - то же для )

15	35	0,9852	0,9791	0,9845	0,62	0,07
20	30	0,7967	0,7519	0,7959	5,62	0,10
30	40	0,1492	0,1238	0,1492	17,02	0,0

Из таблицы видно, что приближение с поправкой Феллера существенно улучшает точность, особенно в ситуации, когда обычное приближение Муавра-Лапласа дает наихудший результат. Последнее наблюдается, когда промежуток выбирается правее среднего значения (на правом хвосте распределения).►