
game_theory
.pdf
2.1.ИГРЫ В РАЗВЕРНУТОЙ ФОРМЕ |
|
|
|
|
61 |
|
выстрел;далее(при условии,что Ржевский остается жив)ход |
ит Оболенский.Решение этой |
|||||
игры показано на рисунке2.9. |
|
|
|
|
|
|
(1811 , 65 ) |
(1511 , 54 ) |
( |
7 |
, 43 ) |
(97 , 32 ) |
(21 , 65 ) |
12 |
||||||
I |
N |
5 |
II |
N |
4 |
I |
|
|
6 |
|
|
5 |
|
|
1 |
|
|
1 |
|
|
|
6 |
|
|
5 |
|
|
N |
3 |
II |
N |
2 |
I |
|
4 |
|
|
3 |
|
1 |
|
|
1 |
|
|
4 |
|
|
3 |
|
|
N |
1 |
II |
|
2 |
(1, 0) |
|
|
|
1 |
|
|
2 |
|
|
(32 , 1) |
(0, 1) |
(1, 32 ) |
(1, 0) |
(32 , 1) |
(0, 1) |
(1, 32 ) |
(1, 0) (23 , 1) |
(0, 1) |
(1, 32 ) |
Рис. 2.9:Игра в русскую рулетку — решение.
На последнем ходе корнет Оболенский предпочтет сдаться,та к как в случае нажатия на курок он погибнет с вероятностью1.Следовательно,при усло вии,что Оболенский сдастся на последнем ходу,ожидаемый выигрыш игроков при нажатии Ржев ским на курок будет (12 , 56 ). Аналогично,при нажатии на курок Оболенским на предыдущем х оде выигрыши будут (79 , 23 ). Продолжая решение таким способом,получим,что Ржевский сд астся при первом же ходе.
Обратная индукция в телеигреSurvivor.
Survivor2 было одним из самых популярных «реалити шоу» на американском телевидении. Первый сезон был показан телекомпаниейCBSлетом2000года. Участники шоу(«племя») находились на необитаемом острове.Задачей каждого было на йти себе пропитание и ночлег. Каждые3дня участники(«совет племени»)решали,кого следу ет изгнать из племени(изгоняемый покидал игру).Перед советом племени все участники п роходили испытание на силу, смекалку или выдержку.Победитель испытания не мог быть изг нан из племени на ближайшем совете.После последнего совета,когда участников осталос ь всего двое,победителя выбирали последние10выбывших участников.
В конце первого сезона в игре оставалось трое человек:Руди, Рич и Келли.Руди,самый старший из участников,был очень популярен и рассчитывал вы игрыть итоговое голосование вне зависимости от того,кто(Келли или Рич)будет изгнан на п оследнем совете племени. Рич и Келли были моложе и имели гораздо больше шансов выиграть последнее перед советом испытание(надо было простоять как можно дольше в неудобной позе,держась одной рукой за тотемный столб).Победитель испытания получал иммуните т и фактическую возможность решать,кого из оставшихся двух участников следует изгнать с острова.
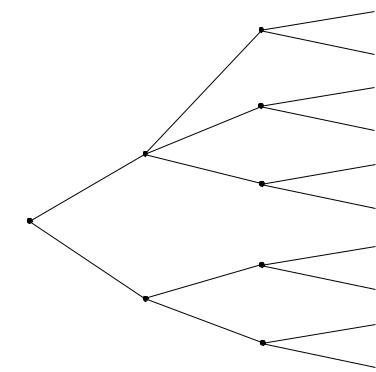
Проблема победителя заключалась в том,что,голосуя против Руди,он рисковал проиграть итоговое голосование,так как Руди был очень популярен сред и выбывших игроков.Лучше было вообще не побеждать в итоговом испытании!Рассмотрим д инамическую игру,в которой на первом этапе один из участников — Рич — решает,стоит ли ему сд аться и намеренно проиграть испытание.Дерево этой игры изображено на рисунке2.10.
В этой игре на последнем ходе Келли и Рич проголосуют против Руди.Если Рича на первом этапе решит «стоять»,то его ожидаемый выигрыш(с учетом рав новесных действий на последнем ходе)будет равен 0.5 ×0.8 + 0.1 ×0 + 0.4 ×0.2 = 0.48.Если Рич решает «сдаться»,то он его ожидаемый выигрыш будет 0.8 × 0.8 + 0.2 × 0 = 0.64.Рич должен уступить,для того,чтобы не быть поставленным перед неудобным выбором.Если бы Рич выиг рал последнее испытание,то он был бы вынужден либо проголосовать против Келли(и затем п роиграть Руди на финальном голосовании),либо проголосовать против Руди(что также на строило бы против него большинство выбывших членов племени).Рич поступил единственным в ерным образом — сдался.Самое
2Этот случай взят из книги Диксита и Скит(2004,стр. 72-77).
62 |
ГЛАВА2.ДИНАМИЧЕСКИЕ ИГРЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ |
-Келли (0,0,1)
Стоять
Рич |
Сдаться
Рич |
-Руди |
(0.2,0.8,0) |
|
|
|
0.4 |
-Рич |
(0,0,1) |
0.1 |
Руди |
-Келли |
(0,0,1) |
|
|
|
|
0.5 |
|
-Руди |
(0.8,0.2,0) |
Природа |
|
|
|
|
Келли |
|
(0,0,1) |
|
|
-Рич |
-Рич (0,0,1)
|
0.2 |
Руди |
-Келли |
(0,0,1) |
Природа |
0.8 |
|
-Руди |
(0.8,0.2,0) |
|
|
Келли |
|
(0,0,1) |
|
|
|
-Рич |
Рис. 2.10:Дерево в игре «Survivor».
примечательное,что Рич не изучал теорию игр,и проделал вес ь путь размышлений под палящим солнцем,стоя в неудобной позе.Расчет оказался прави льным:соревнования выиграла Келли,которая затем проголосовала против Руди.Выбывшие ч лены племени проголосовали против Келли,что сделало Рича победителем всей игры.
Ограничение метода обратной индукции:игры «сороконожка» и «ультиматум».
Следующие два примера — «паталогические» динамические игры,в которых предсказанное
равновесие,полученное |
обратной индукцией,не соответств ует как нашим представлениям |
о том,как будут вести |
себя люди в аналогичных ситуациях,так и данным,полученным в |
ходе экономических экспериментов.В каждой из игр причина р асхождения между теорией и действительностью разная.В первом случае — игре «сорокон ожка» — поведение игроков отличается от равновесного,поскольку нахождение равнове сия требует большего числа шагов алгоритма обратной индукции.Во втором случае — игре «ульти матум» — денежные выигрыши игроков не отражают их истинных предпочтений,на которые мо гут влиять такие факторы, как представления о справедливости,зависть,или альтруиз м.
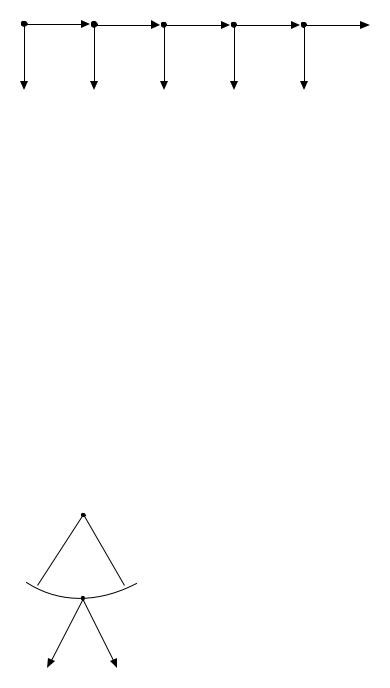
Сороконожка. Богатый мизантроп позвал в гости двух студентов:Вову и Диму .Он предлагает Вове взять один рубль.Если он отказывается,то Диме п редлагается2рубля.Если Дима отказывается,то Вове предлагается взять4,и так далее.Нак онец,Вове предлагается либо забрать16рублей,либо поделить эту сумму поровну между собой и Димой.Дерево этой игры представлено на рисунке2.11.
Решая игру методом обратной индукции,мы приходим к неутеши тельному выводу:в самом начале игры Вова заберет один рубль;Дима не получит ничего.
Игра «сороконожка» показывает,что обратная индукция не вс егда дает хороший прогноз человеческого поведения.Действительно,если бы вам предл ожили поиграть в «сороконожку», то вы вряд ли бы остановили игру на первом ходе.В ходе экспери мента,проведенного Мак-
2.1.ИГРЫ В РАЗВЕРНУТОЙ ФОРМЕ |
63 |
V |
D |
V |
D |
V |
|
(8,8) |
(1, 0) |
(0, 2) |
(4, 0) |
(0,8) |
(16,0) |
|
|
|
Рис. 2.11:Игра «сороконожка». |
|
кельви и Полфри(1992),более60%игроков останавливались н а3или4ходе из7возможных. Однако дальнейшие исследования показали,что результат эк сперимента сильно зависит от
интеллектуального уровня игроков.Обычно,в качестве субъ |
ектов экперимента используют |
университетских студентов.Паласиос-Уэрта и Волиш(2009) |
провели тот же эксперимент с |
шахматистами высокого уровня.Результаты разительно отли чались:в большинстве случаев, игра останавливалась на первом же ходе;при этом,вероятнос ть остановки на первом ходе возрастала с шахматным рейтингом игроков(гроссмейстеры в сегда прекращали игру при первой же возможности).Показательно,что склонность игра ть равновесные стратегии зависит не только от собственного уровня,но и от уровня соперника:е сли обычный игрок знает,что он играет против профессионального шахматиста,то его собств енное поведение будет больше соотвествовать равновесному,чем в том случае,когда он играе т против другого обычного игрока.
Ультиматум. Олег предлагает Михаилу пропорции,в которых можно поделит ь100рублей. Пусть Олег предлагает оставить p [0, 100] рублей себе,и оставить 100 − p Михаилу.Если Михаил соглашается( A),то эти платежи реализуются.Если он отказывается( D),то каждый игрок получает0.На рисунке2.12изображено дерево этой игр ы.
O |
p [0, 100]
k
M
A D
(p, 100 − p) (0, 0)
Рис. 2.12:Игра «ультиматум».
Как поступит Михаил при известном p?Если p < 100,то Михаил согласится,так как 100 − p > 0.Если p = 100,то Михаил может и согласиться,и отказаться(его выигрыш бу дет равен нулю в обоих случаях).При условии,что реакция Михаила буде т такой,Олег предложит дележ p = 100 − ϵ, где ϵ > 0 — небольшая величина.Михаил согласится на такой дележ.
Игра «ультиматум» — еще один пример того,как результат,пол ученный методом обратной индукции,не реализуется в реальной игре.Эта игра,как и «со роконожка»,часто исследуется в экономических экспериментах,и результаты,как правило, также разительно отличаются от полученного выше равновесия.Первая причина состоит в том, что второй игрок,как правило, отвергает дележ,который он считает несправедливым.В неко торых экспериментах,вторые игроки отвергали дележи,предлагавшие им вплоть до половин ы от имевшейся у первого игрока суммы.Первый игрок,предвидя это,«делится»(Камерер, 200 3).
64 ГЛАВА2.ДИНАМИЧЕСКИЕ ИГРЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ
Второй причиной,почему экспериментальные результаты отл ичаются от предсказанных моделью p = 100 − ϵ,является альтруизм.Хоффман и др. (1996)исследовали так н азываемую «игру диктатора»,в которой игрок,обладающий определенно й суммой денег,может поделиться частью этой суммы с неизвестным ему реципиентом.При этом ре ципиент,в отличие от второго игрока в «ультиматуме»,не имеет возможности отказать ся или заблокировать дележ.В эксперименте, 46%диктаторов пожертвовали не менее$3из им еющихся у них$10,при том, что им не была известна личность реципиентов.В той же работе ,однако,было показано,что
при альтернативных условиях эксперимента,когда личности |
«диктаторов» не известны экспе- |
риментаторам,пожертвования резко сокращаются(до16%).А |
вторы мотивируют это тем,что |
когда человеку известно,что за его альтруистическими дейс твиями никто не наблюдает,у человека меньше стимулов делиться с неизвестным ему человеком.Однако в других работах было показано,что на степень альтруизма влияет большое число фа кторов — таких,как ожидаемое состояние реципиента(бедным дают больше),восприятие сре дств,имеющихся у диктатора(человек с меньшей вероятностью поделится,если воспринимает свои деньги как заработанные,а не как подарок),и так далее.Человеческое поведение в играх типа «ультиматум» и «диктатор» до конца не изучено и продолжает оставаться актуальной темой для исследований.
2.1.4Смешанные стратегии в динамической игре
Как нам определить смешанные стратегии для игр в развернутой форме?Конечно же,можно просто расширить множество чистых стратегий до множества распределений вероятности на
нем.Формально,множеством смешанных стратегий игрока |
i будет |
Σi = ∆|×hi Hi A(hi)|−1, |
(2.2) |
где,как мы помним, ×hi Hi A(hi) есть множество чистых стратегий,то есть множество всех возможных комбинаций действий игрока во всех его информационных множествах.
Какой длины вектор необходим,чтобы задать смешанную страт егию?В игре «лобовая атака»,смешанная стратегия для Михаэля Шумахера будет сос тоять из вероятностей p1, p2, p3, и 1 − p1 − p2 − p3,с которыми он будет играть свои чистые стратегии(см.табли цу2.1).Для Ивана смешанная стратегия будет определяться вероятностями q и 1 − q.
|
|
|
|
Михаэль |
|
|
|
|
|
|
|
TT |
TN |
NT |
NN |
|
|
|
|
Иван |
T |
0,0 |
0,0 |
-1,1 |
-1,1 |
|
q |
|
|
N |
1,-1 |
-2,-2 |
1,-1 |
-2,-2 |
|
1 − q |
|
||
|
|
|
|||||||
|
|
p1 |
p2 |
p3 |
1 − p1 − p2 − p3 |
|
|
|
|
|
|
|
Таблица2.1:Петр и Михаэль:смешанные стратегии |
||||||
В общем случае,длина вектора,определяющего смешанную стр |
атегию,будет равна числу |
||||||||
чистых стратегий минус1: |
|
' |
|
|
|||||
|
|
|
|
|
|
|
(2.3) |
||
|
|
|
|
|
dim(Σi) = |
|
|A(hi)| − 1. |
||
hi Hi
Здесь dim(·) означает размерность множества.Так,у Шумахера смешанная стратегия задается тремя параметрами p1, p2, и p3.Случайное поведение игроков можно задать и более простым способом.Предположим,что Михаэль и Иван играю т смешанные стратегии (p1, p2, p3, 1 −p1 −p2 −p3) и (q, 1 −q).Давайте посчитаем вероятность того,что Михаэль свернет
(то есть выберет действие T) в том случае,если Иван свернет(выберет действие |
T). Легко |
проверить,что эта величина есть |
|
p1′ = p1 + p2. |
(2.4) |

2.1.ИГРЫ В РАЗВЕРНУТОЙ ФОРМЕ |
65 |
Аналогично,в том случае,если Иван не свернет,Михаэль свор |
ачивает с вероятностью |
p2′ = p1 + p3. |
(2.5) |
Вероятности (p′1, p′2) являются поведенческой стратегией Михаэля. Дадим формальное определение.
Определение18 Множество поведенческих стратегий игрока i есть
Bi = ×hi Hi ∆|A(hi)|−1. |
(2.6) |
Поведенческая стратегия предписывает,для каждого информ ационного множества,с какой вероятностью нужно выбирать каждое из действий.Исследова ть игру с помощью поведенческих стратегий значительно проще,чем с помощью смешанных. Действительно,
|
( |
(2.7) |
dim(Bi) = |
(|A(hi)| − 1). |
|
|
hi Hi |
|
Если у игрока3информационных множества,в которых возможн |
о по3, 4и5действий,то |
|
размерность вектора поведенческой стратегии будет равно 3 + 4 + 5 − 3 = 9,а размерность вектора смешанной стратегии — 3 × 4 × 5 − 1 = 59.
Определим,как в общем случае получать поведенческие страт егии из смешанных.Если Ri(hi) — множество чистых стратегий игрока i,допускающих прохождение игры через инфор-
мационное множество hi при каких-то s−i,то вероятность того,что игрок |
i выберет действие |
||||
ai в информационном множестве hi,есть |
& |
|
|
|
|
bi(ai|hi) = |
i |
si Ri(hi) σi(si) |
. |
(2.8) |
|
|
s |
|
Ri(hi),si(hi)=ai σi(si) |
|
|
&
Здесь, σi(si) — вероятность сыграть чистую стратегию si при смешанной стратегии σi.Обозначим за bi(σi) поведенческую стратегию,полученную таким образом из смеш анной стратегии σi (в качестве примера — (p′1, p′2)).Обозначим за σi(bi) множество всех смешанных стратегий, приводящих к поведенческой стратегии bi.
Имеется следующий результат.
Теорема6 (Кун, 1953).Для всех игр с полной памятью,смешанные и повед енческие стратегии эквивалентны.То есть для всех σi, σ−i,мы имеем
ui(σi, σ−i) = ui(bi(σi), b−i(σ−i)), |
(2.9) |
а для всех bi, b−i и всех σi σi(bi),σ−i σ−i(bi) —
ui(σi, σ−i) = ui(bi, b−i). |
(2.10) |
В игре с полной памятью каждый игрок,в каждом информационно м множестве,помнит всю последовательность сделанных им ходов,а также не забывает все однажды увиденные им ходы других игроков.Подавляющее большинство игровых взаимоде йствий в экономике,политологии и других общественных науках,являются играми с полной памя тью.
Рассмотрим пример игры без полной памяти.Водитель едет дом ой в слегка нетрезвом состоянии(рисунок2.13).На дороге два поворота,на которых м ожно повернуть направо( R) или поехать прямо( S).Водителю нужно повернуть направо на втором повороте.Но п роехав первый поворот,он тут же забывает,что его проехал.

66 |
ГЛАВА2.ДИНАМИЧЕСКИЕ ИГРЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ |
S |
S |
|
0 |
R |
R |
0 |
4 |
Рис. 2.13:Незадачливый шофер
В игре две чистые стратегии: R и S. Обе приносят нулевой выигрыш.Соответственно,выигрыш при любой смешанной стратегии тоже будет нулевым:если и грок с вероятностью p всегда сворачивает(то есть играет чистую стратегию R),и с вероятностью 1 − p никогда не сворачивает(чистая стратегия S),то его ожидаемый выигрыш будет 0 · p + 0 · (1 − p) = 0.Если же игрок принимает поведенческую стратегию «при любой возможности,поворачивать направо с вероятностью p»,то его ожидаемый выигрыш будет 0 · p + (1 − p) · (4 · p + 0 · (1 − p)) = 4p(1 − p). Поведенческая стратегия p = 12 принесет ему ожидаемый выигрыш,равный 1.Следовательно, в этой игре смешанные и поведенческие стратегии не эквивалентны.
Верю-не верю.
В колоде,рубашкой кверху,лежат две карты:шестерка и туз.П |
ервый игрок берет одну кар- |
ту,смотрит ее,и называет ее достоинство(6или туз).Если пе |
рвый игрок сказал «6»,то он |
проигрывает второму игроку1рубль.Если первый игрок сказа |
л «туз»,то второй игрок мо- |
жет поверить или не поверить.Если второй игрок поверил,то о н проигрывает первому игроку
1рубль.Если второй игрок не поверил,то первый игрок открыв |
ает карту.Если это туз,то |
первый выигрывает2рубля.Если это шестерка,то первый игро |
к проигрывает2рубля. |
Природа |
6 Туз
Игрок1
«6» |
«Туз» «Туз» |
«6» |
-1,1 |
Игрок2 |
1,-1 |
|
|
В |
Н |
В |
Н |
1,-1 |
-2,2 |
1,-1 |
2,-2 |
Рис. 2.14:Игра верю-не верю
Дерево этой игры показано на рисунке2.14.Первый ход делает Природа — она решает, какую карту получит первый игрок.У первого игрока два инфор мационных множества,и, соответственно,четыре стратегии.Однако любая стратегия ,которая предписывает заявлять «6» при наличии туза,слабо доминируется стратегией,котор ая при наличии туза предписывает говорить «туз».Поэтому поведенческой стратегией Игрока1 будем считать p — вероятность того,что этот игрок заявит «туз» при условии,что у него на ру ках шестерка.Стратегия игрока 2— вероятность q сказать «не верю».Выразим ожидаемые выигрыши обоих игроко в через p и

2.1.ИГРЫ В РАЗВЕРНУТОЙ ФОРМЕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
67 |
||||||||
q: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
(p, q) |
= |
− |
1 − p |
− |
2q |
p |
+ (1 |
− |
q) |
p |
+ 2 |
|
1 |
q + |
1 |
(1 |
− |
q) = p |
− |
3 |
pq + |
q |
, |
|
|
2 |
2 |
2 |
|
|||||||||||||||||||
1 |
|
|
2 |
2 |
|
2 |
|
|
|
|
2 |
(2.11) |
||||||||||||
u2 |
(p, q) |
= |
−u1(p, q). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Равновесием Нэша в этой игре является p = 13 , q = 23 .Равновесные стратегии в игре «верюне верю» являются смешанными.Действительно,если второй и грок всегда верит,то первому игроку будет выгодно всегда говорить «туз».В таком случае, второй игрок должен все время проверять карту первого игрока.Однако же если второй игрок всегда проверяет,то первый игрок должен всегда говорить «6»,получив шестерку.Но тогд а,если первый игрок никогда не врет,второму нет смысла проверять его карту!По сути,мы и меем игру типа однопериодной игры «инспекция».Очередность ходов здесь компенсируе тся асимметричной информацией: первый игрок знает,какая карта у него на руках,а второй — нет .
2.1.5Совершенство по подыграм
Метод обратной индукции можно использовать не только для игр с совершенной информацией. Дадим такое определение.
Определение19 Пусть Γ — игра в развернутой форме. Подыгра Γ(x) — это часть дерева игры, которая начинается с некоторой вершины x,и удовлетворяет следующим свойствам:
1. x — единственный элемент в своем информационном множестве.
2.Информационные множества,содержащие вершины из подыгр ы Γ(x),не содержат других вершин.
Приведем пример — вариацию на тему игры «сжигание мостов».Генерал должен защищать город на берегу реки.До того,как враг нападает,генерал при нимает решение,сжигать мост, соединяющий город с другим берегом( B),или нет( N).На этот раз враг не является игроком,и нападает автоматически.Далее командиры двух отрядов(под чиненные генерала)принимают решение:бежать с поле боя( R),или нет( F).В случае,когда мост не разрушен,выигрыши командиров в зависимости от принимамых ими решений таковы:
|
КомандирII |
||
|
|
R |
F |
КомандирI |
|
|
|
R |
3,3 |
5,2 |
|
|
F |
2,5 |
4,4 |
|
|
|
|
Если мост уничтожен,то отступающему отряду придется навод ить переправу во время боя. Выигрыши командиров тогда будут
|
КомандирII |
||
|
|
R |
F |
КомандирI |
|
|
|
R |
1,1 |
3,2 |
|
|
F |
2,3 |
4,4 |
|
|
|
|
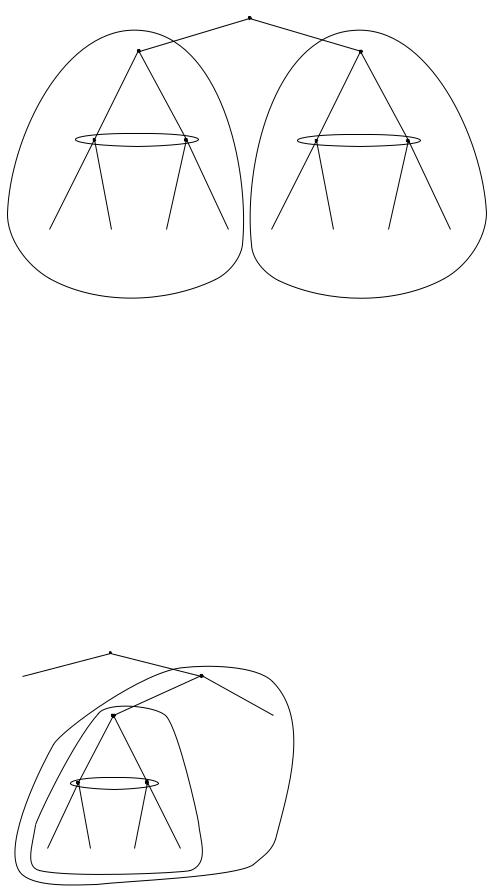
Наконец,выигрыш генерала равен1,если город остался защищ ать хотя бы один отряд,и 0,если оба отряда бежали.Дерево этой игры показано на рисун ке2.15.
Формально,эта игра не является игрой с совершенной информа цией,так как после первого хода генерала,два командира принимают решения одновремен но.Однако эту игру можно решить способом,очень похожим на метод обратной индукции,ис пользуемый нами для решения игр с совершенной информацией.У нас две подыгры,соответст вующие каждому из двух возможных действий генерала.В первой подыгре,когда мост не со жжен,равновесный профиль
68
I |
ГЛАВА2.ДИНАМИЧЕСКИЕ ИГРЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ
|
Генерал |
|
B |
N |
I |
|
|
|
R |
F |
|
|
R |
F |
|
|
|
II |
|
|
|
II |
|
R |
F |
R |
F |
R |
F |
R |
F |
0,1,1 |
1,3,2 |
1,2,3 |
1,4,4 |
0,3,3 |
1,5,2 |
1,2,5 |
1,4,4 |
Рис. 2.15:Сжигание мостов- 2.Подыгры выделены пунктиром.
стратегий первого и второго командира будет (R, R).Во второй подыгре,когда мост сожжен, равновесие будет (F, F).Следовательно,генерал получает выигрыш 0,если делает ход N, и 1, если делает ход B.Дадим определение равновесия,которое мы получили.
Определение20 Пусть Γ — динамическая игра.Профиль стратегий является совершенным по подыграм, если он является равновесным для каждой из подыгр Γ.
Любое равновесие,полученное методом обратной индукции,я вляется совершенным по подыграм.
В игре «лобовая атака» две подыгры.В каждой подыгре Иван при нимает решение,свернуть ему,или нет.Каждая подыгра соответствует одному из решени й Петра(свернуть/не свернуть). В игре «ультиматум» континуум подыгр,по одной для каждого p [100].В каждой подыгре Михаил решает,согласиться ему или отказаться с предложенн ым дележом.
Пример. На рисунке2.16показана игра из работы Рабина(1988)и учебн ика Фаденберга и Тироля(1991,стр.99-100).
ИгрокI
L  R
R
(6, 0, 6) |
L |
|
ИгрокI |
F G
ИгрокII |
R |
(8, 6, 8)
ИгрокIII |
F G F G
(0, 0, 0) (7, 10, 7) (7, 10, 7) (0, 0, 0)
Рис. 2.16:Координация или нет?
У этой игры две подыгры(показаны пунктиром).Подыгра2явля |
ется игрой в координацию |
между игрокамиIиIII.У этой игры три равновесия.Два из них в |
чистых стратегиях,дающих |

2.1.ИГРЫ В РАЗВЕРНУТОЙ ФОРМЕ |
69 |
выигрыш (7, 10, 7) и одно — в смешанных,которое дает выигрыш (3.5, 5, 3.5).Если в подыгре 2играется одно из двух координационных равновесий( (F, G) либо (G, F)),то игрокIIдолжен
делать ход L.Если в подыгре2играется равновесие в смешанных стратегия |
х(то есть игроки |
||
IиIIIне координируют свои действия),то игрокIIдолжен сде |
лать ход R.Следовательно, |
||
в подыгре1выигрыш игрокаIсоставит либо7,либо8,то есть ег |
о первый ход всегда будет |
||
R.В итоге это дает нам три совершенных по подыграм равновесия : ((R, G), L, F), ((R, F), L, G) и |
|||
((R, 21 G + 21 F), R, 21 G + 21 F). |
|
|
к I не |
Может ли ход L быть разумным с точки зрения игрокаI?Пусть,например,игро |
|||
может координировать свои действия с игрокомIIIв подыгре2 |
.Если игрокIIоб этом не знает |
||
(и думает,чтоIиIIIбудут координироваться),то в итоге выи |
грыши игроков в подыгре1 |
||
составят (3.5, 5, 3.5).В этом случае игрокуIв начале игры надо сделать ход |
L.Таким образом, |
||
понятие совершенства по подыграм предполагает не только то,что все игроки ожидают,что во всех подыграх будут реализовываться равновесия Нэша,но и то,что во всех подыграх ожидаются одни и те же равновесия(Фаденберг и Тироль, 1991, стр. 100).
2.1.6Примеры.
Модель ценовой конкуренции Штакельберга.
Рассмотрим модель ценовой конкуренции из Главы1.В стране N два производителя виджетов.Обе фирмы должны решить,сколько штук виджетов произве сти в течение ближайшего месяца.Пусть q1 [0, ∞) — объем производства первой фирмы, q2 [0, ∞) — второй.Пусть взаимодействие фирм реализуется в2этапа.
1этап. Фирма1выбирает q1.
2этап. Фирма2выбирает q2.
Как и раньше,функция спроса на виджеты имеет вид P = 1 − q1 − q2, где P — максимальная цена,по которой удастся продать q1 + q2 штук в течение месяца.Предположим,что издержки производства у фирмы i равны cqi, где 0 ≤ c < 1.Прибыль фирмы равна ее выручке за вычетом издержек производства:
u1 |
= |
q1P − q1 = q1(1 − q1 − q2) − cq1 |
(2.12) |
u2 |
= |
q2P − q2 = q2(1 − q1 − q2) − cq2. |
Найдем совершенное по подыграм равновесие.В этой игре для к аждого q1,выбранного
первой фирмой,определяется подыгра,в которой фирма2выби |
рает q2.Решением максимиза- |
|||||
ционной задачи Фирмы2будет |
|
|
|
|
|
|
$ |
|
1−q1−c |
, |
|
|
(2.13) |
|
|
q1 |
≥ 1 − c, |
|||
0, |
||||||
q2(q1) = |
2 |
q1 |
< 1 − c |
|||
Уравнение(2.13)задает стратегию игрока2в совершенном по |
подыграм равновесии.Теперь |
|||||
необходимо найти q1,который максимизирует выигрыш первого игрока при условии , что второй игрок выбирает стратегию(2.13).Подставим q2(q1) в u1:
u1(q1, q2(q1)) = |
q21 (1 |
− q1 |
− c), |
q1 |
< 1 |
− c, |
(2.14) |
|
$ q1(1 − q1 − c), |
q1 ≥ 1 − c. |
|
||||
Максимизируя u1(q1, q2(q1)) по q1, получим q1 = 1−2 c , q2(q1) = 1−4 c .Заметим,что это решение отличается от равновесия в игре Курно,в которой обе фирмы хо дят одновременно(тогда мы имеем q1 = q2 = 1−3 c ).Возможность делать первый ход дает фирме1преимущество: в модели Штакельберга ее прибыль выше,чем в модели Курно.При этом пр ибыль фирмы2будет ниже.

70 |
ГЛАВА2.ДИНАМИЧЕСКИЕ ИГРЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ |
Модель ценовой конкуренции с инвестициями в производственные мощности.
Постановка модели Штакельберга вызывает ряд вопросов.Поч ему в какой-нибудь отрасли у одной из фирм будет преимущество,позволяющее ей первой реш ать,сколько производить?Что вообще означает «выбор объемов производства»?В долгосроч ной перспективе,количество товара,производимого фирмой,определяется ее производстве нными мощностями.Если фирма хочет увеличить объем производства,то она должна построит ь новый завод.При этом начальные условия у фирм могут быть разными.Одна из фирм может обла дать преимуществом, позволяющим ей первой принимать решение относительно того,какого размера завод следует построить.Например,фирма может первой разработать техно логию производства нового товара;обладать б´ольшими финансовыми возможностями;обла дать необходимым административным ресурсом.Фирма,которая уже построила завод,облад ает более низкими предельными издержками по сравнению с фирмой,которой только предстоит принять решение о том,какого размера завод ей предстоит построить(и,соответственно,с колько товара производить).Такова интерпретация классической(Штакельберг, 1934)модели це новой конкуренции,предложенная Спенсом(1977)и Дикситом(1979, 1980).Ниже представлена м одель ценовой конкуренции между двумя фирмами,взятая из работы Диксита(1980). 3
Предположим,что две фирмы играют в динамическую игру со сле дующим порядком ходов:
1этап. Фирма1выбирает q¯1 — установленную мощность перед тем,как на рынок войдет
Фирма2. |
|
|
|
|
2этап. Фирмы1и2выбирают |
q1, q2 — объемы производства. |
|
||
Функции полезностей двух фирм при этом будут |
|
|||
U1 |
= |
P q1 |
− cq¯1 − c · max{0, q1 − q¯1}, |
(2.15) |
U2 |
= |
P q2 |
− cq2, |
|
где 0 < c ≤ 12 — стоимость установленной мощности,позволяющей производ ить1единицу товара за указанный период.Пусть,как и прежде, P = 1−q1 −q2.Таким образом,мы предполагаем, что на втором этапе предельные издержки Фирмы1равны 0 при q1 < q¯1 и c при q1 > q¯1, так как затраты на строительство завода на первом этапе являются невозвратными.Предельные издержки фирмы2всегда равны c.
Решение задачи максимизации полезности на втором этапе дает нам следующую функцию
реакции для первой фирмы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
q |
2 |
≥ |
1, |
|
|
|
|
|
|
1 |
|
q2 |
|
|
|
|
|
|
|
|||
q1(q2) = |
|
−2 |
, |
q2 |
|
[1 |
− |
2¯q1, 1), |
|
(2.16) |
|||
|
q¯1, |
|
q2 |
[1 |
2¯q1 c, 1 2¯q1), |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
− |
q2 |
c |
|
|
|
|
− |
− |
− |
|
|
|
|
2 |
− |
, q2 < 1 − 2¯q1 − c. |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для второй фирмы функция реакции будет такой же,как и в задач ах Курно и Штакельберга:
q2 |
(q1) = |
0, |
|
|
|
q |
1 ≥ |
1 |
− |
c, |
(2.17) |
|
1 |
|
q1 |
|
c |
|
|
|
|||||
|
$ |
|
− |
2 |
− |
, q1 < 1 − c. |
|
|||||
Нам нужно найти решение системы |
|
|
|
|
|
|
|
|
|
|
|
|
|
q1(q2) = q1, |
q2(q1) = q1 |
|
(2.18) |
||||||||
для всех возможных значений q¯1.Так как графики функций реакции пересекаются ровно в одной точке,решение единственно.Всего возможно три случа я(рисунок2.17).
3Обзоры таких работ содержатся в книге Тироля(1987,стр. 314 ) и Вивеса (1999, гл . 7).
