
game_theory
.pdf3.1.БАЙЕСОВЫ ИГРЫ |
111 |
Понятие байесовой игры было введено Харшаньи(1967-1968). Он предложил интерпретировать игру с неполной информацией как игру с полной информацией с большим количеством игроков,в которой каждый игрок соответствует одному типу и грока в исходной игре.Первый ход делает Природа,определяя,какой тип каждого игрока буд ет задействован.Например,если каждый из двух игроков имеет два типа,то такую статическую и гру можно представить как динамическую игру между четырьмя игроками,в которой каждый игрок соответствует одному игроку и одному типу в исходной игре.
Определение28 Пусть I, A, T, P, u — байесова игра.Равновесием в этой игре является набор
стратегий s ,такой,что для всех i,для всех |
ai′ Ai, ti Ti, |
|
( |
P (t−i|ti)ui(ai′, s−i(t−i), ti). |
|
u˜i(s (·), ti) ≥ |
(3.5) |
t−i T−i
Равновесие в такой игре называется Байесовым равновесием или равновесием Байеса-Нэша.
Это определение эквивалентно определению равновесия Нэша для представления байесовой игры,в котором первой ход делает Природа,выбирая тип игрок ов.Из теоремы о существовании равновесия в конечных играх следует следующее утверждение:
Теорема10 Пусть G = I, A, T, P, u ,причем множества I, A и T конечны.Тогда в этой игре существует равновесие s .
Дуополия Курно с неполной информацией
Вернемся к задаче конкуренции двух фирм,рассмотренной в пе рвой главе.Две фирмы решают, сколько товара произвести на продажу.Прибыль каждой фирмы равна ее выручке за вычетом издержек:
U1 |
= P q1 |
− c1q1 |
(3.6) |
U2 |
= P q2 |
− c2q2, |
(3.7) |
где P = 1 − q1 − q2 — функция спроса.Пусть c1 известен обеим фирмам.Напротив, |
c2 является |
||
частной информацией.Он известен только Фирме2.Первой фир ме известно лишь,что эта величина принимает значение cH с вероятностью θ и cL с вероятностью 1 − θ.При этом мы предполагаем,что θ является всеобщим знанием — то есть второй фирме известно θ,первой фирма известно,что второй фирме известно θ,и так далее.
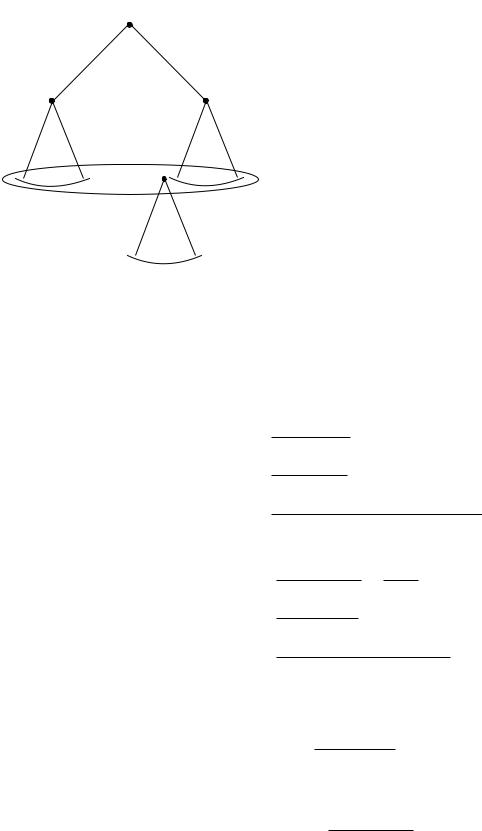
В этой игре мы имеем T = {H, L}.Дерево игры представлено на рисунке3.1.
Что является равновесием в этой игре?Фирма1обладает тольк о одним возможным уровнем издержек.Следовательно,в равновесии в чистых стратегиях она будет производить какое-то количество товара q1.У Фирмы2возможно два уровня издержек;следовательно,нам необходимо найти q2(H) и q2 (L) — равновесные выпуски второй фирмы в том случае,когда ее изд ержки высокие и низкие,соответственно.
Согласно определению,равновесное действие каждой фирмы д олжно удовлетворять следующим условиям:
1. q2(H) есть решение задачи
max u2(q1, q2, H) = (1 − q1 − q2 − cH )q2
q2
2. q2(L) есть решение задачи
max u2(q1, q2, L) = (1 − q1 − q2 − cL)q2
q2
112 |
ГЛАВА3.СТАТИЧЕСКИЕ ИГРЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ |
θ, c2 = cH |
q2
Природа |
1 − θ, c2 = cL
Фирма2
q2 |
Фирма1 |
q1
Рис. 3.1:Дерево игры в дуополии Курно с неполной информацие й.
3. q1 есть решение задачи
max u˜1(q1, q2(L), q2(H)) = θ(1 − q1 − q2(H) − c1)q1 + (1 − θ)(1 − q1 − q2 (L) − c1)q1.
q1
Решая эти максимизационные задачи,получим условия первог о порядка
q (H) = |
1 − q1 − cH |
|
|
|
|
|
|
|
|
||||
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q (L) = |
1 − q1 − cL |
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
− |
θq (H) |
− |
(1 |
− |
θ)q (L) |
− |
c |
1 |
|
||
q1 |
= |
|
2 |
|
2 |
2 |
|
. |
|||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.8)
(3.9)
(3.10)
Решение этих уравнений дает нам |
|
|
|
|
|
|
|
|
|
|
|
|
q (H) = |
1 |
− 2cH + c1 |
+ |
|
1 − θ |
(cH |
− |
cL) |
(3.11) |
|||
|
||||||||||||
2 |
|
3 |
|
6 |
|
|
|
|
||||
q (L) = |
1 |
− 2cL + c1 |
− |
|
θ |
(cH |
− |
cL) |
|
(3.12) |
||
|
6 |
|
||||||||||
2 |
|
3 |
|
|
|
|
|
|
||||
q1 = |
1 |
− 2c1 + θcH + (1 − θ)cL |
. |
|
(3.13) |
|||||||
|
|
|||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
Интересно сравнить равновесный объем производства каждой из фирм в случае полной и неполной информации.Как мы помним,при полной информации в равно весии в модели Курно мы
имеем
q2 = 1 − 2c2 + c1 .
3
Таким образом,объем производства второй фирмы в случае,ес ли ее издержки высокие,будет выше при неполной информации:
q2(H) > |
1 − 2cH + c1 |
|
3 |
Получается,что на равновесие влияют не только издержки Фир мы2,но и тот факт,известно
ли Фирме2,что Фирма1знает издержки Фирмы2.Если Фирма1не з |
нает точного уровня c2, |
то ее равновесный выпуск будет ниже,чем в том случае,когда е |
й известно,что c2 = cH (так |
как в первом случае,Фирма1будет ожидать,что с вероятность |
ю 1 − θ издержки Фирмы2 |
будут низкими,а ее выпуск — высоким).Фирма2,предвидя это, |
будет производить больше, |
чем в случае с полной информацией. |
|

3.1.БАЙЕСОВЫ ИГРЫ |
113 |
Электоральная активность
Почему люди голосуют на выборах?Ведь голосование сопряжен о с издержками — потерей времени,которое можно потратить на работу или отдых,а шансов к ак-то реально повлиять на исход выборов очень мало.Тем не менее,явка на выборах федер ального уровня в большинстве стран превышает50%,то есть люди идут голосовать вопреки те оретическим прогнозам.Этот факт продолжает доставлять много неудобства исследователям,так как теоретико-игровые модели предсказывают,что явка на выборах должна быть крайн е низкой.Построение адекватной модели принятия решения «голосовать или остаться дома» остается пока нерешенной теоретической задачей,показывающей ограничения теорети ко-игрового анализа человеческого поведения.1
Действительно,пусть в выборах участвуют два кандидата,и и збиратель решает,голосовать на выборах за своего любимого кандидата,или нет.Пусть B — дополнительный выигрыш, который избирателю сулит победа его любимого кандидата, P — вероятность того,что голос избирателя будет решающим(то есть голоса всех остальных из бирателей будут поровну отданы за обоих кандидатов,будем считать,что других избирателей четное число,и все они голосуют за того или другого кандидата).Наконец,пусть c — издержки,связанные с голосованием.В
таком случае,избиратель должен проголосовать,только есл |
и |
U = P B − c ≥ 0. |
(3.14) |
На настоящих выборах,величина B может составлять существенную часть дохода избирателя на протяжении следующего электорального цикла — то есть равняться его заработной плате за несколько недель или даже месяцев(в особенности если раз ные кандидаты предлагают разную налоговую политику и разный объем субсидий различным группам граждан).Так как в большинстве случаев голосование не требует много времени, величина c не должна превышать значение часовой зарплаты человека.Однако простые расчет ы показывают,что при реалистичных предположениях значение p настолько мало,что участие избирателя в выборах не будет оправдано.Получается так называемый «парадокс голосован ия».2
Рассмотрим однопериодную игру,в которой участвуют N1 + N2 индивидов — избирателей. Каждый избиратель решает,стоит ли ему проголосовать за одн ого из двух кандидатов( A или B),либо остаться дома: Si = {A, B, o}.Предположим,что избиратели делятся на две группы
численностью N1 и N2.Каждый избиратель,принадлежащий к первой группе,в случа |
е победы |
на выборах кандидата A получает выигрыш,равный1,а в случае победы кандидата |
B, не |
получает ничего.Каждый избиратель второй группы аналигич ным образом предпочтет,чтобы победил кандидат B.Таким образом,вероятность победы кандидата A есть
PA = |
|
2 , |
# i si |
= A |
} |
= # i si = B |
|
(3.15) |
||||||||||||||
|
|
|
1 |
|
{ |
i |
| |
i |
= A |
> # |
{ |
i |
| |
s |
i = B} |
|
||||||
|
|
|
1, # |
|
|
s |
|
|
|
|
|
}, |
|
|||||||||
|
|
0, #{i|si |
= A} |
< #{i|si = B |
|
|||||||||||||||||
|
|
|
|
|
{ | |
|
|
|
} |
P |
|
{ | |
|
|
} |
|
||||||
вероятность победы второго |
кандидата есть P |
|
= 1 |
|
|
.В случае,если избиратель |
i голосует |
|||||||||||||||
|
|
|
|
|
|
|
|
B |
|
|
− |
|
A |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||
за одного из двух кандидатов,он несет издержки ci < |
2 . |
|
|
|
|
|
|
|||||||||||||||
Мы попробуем найти равновесие в этой игре для двух случаев — когда издержки каждого избирателя являются публичной информацией,и когда они изв естны только самому избира-
1Обзор литературы поэтой теме можно найти,например,в учебн ике Мюллера(2007,гл. 14).
2Если предположить,что каждый из остальных избирателей гол осует с вероятностью q за первого кандидата,
|
|
|
|
P = 3e |
−2(N−1)(p−0.5)2 |
||||||||
то вероятность того,что голос данного избирателя будет реш ающим,будет приблизительно |
2√ |
|
|
|
|
||||||||
2π(N |
− |
1) |
|
||||||||||
(согласно Оуэну и Грофману, 1984).Если |
|
1 |
, то эта величина будет пропорциональна |
1 |
|
|
|
|
|
||||
q = |
, |
то есть при |
|||||||||||
2 |
√ |
|
|||||||||||
N |
|||||||||||||
миллионе избирателей вероятность стать решающим будет одна тысячная.Это не так мало — однако если q ̸= 12 , то картина резко меняется ; уже приq = 0.505 и N = 1000000, мы будем иметь P 10−25 — нулевая вероятность со всех практических точек зрения.
114 |
|
ГЛАВА3.СТАТИЧЕСКИЕ ИГРЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ |
|
||||||||||
телю.Мы покажем,что хотя в первом случае и может существова |
ть равновесие,в котором |
|
|||||||||||
вероятность явки каждого избирателя высока,во втором случ ае явка будет обязательно низ- |
|
||||||||||||
ка3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим сначала случай с полной информацией.Пусть изде ржки у всех избирателей |
|
||||||||||||
одинаковы: ci = c.Предположим также,что обе группы избирателей имеют одина |
ковый раз- |
|
|||||||||||
мер: N1 = N2 = N.Заметим,что для избирателей первой группы стратегия |
si |
= B слабо |
|
||||||||||
доминируется стратегией si = A,а для избирателей второй группы,наоборот, Si |
= A слабо до- |
|
|||||||||||
минируется si = B.Следовательно,мы будем предполагать,что у каждого избир |
ателя только |
|
|||||||||||
две стратегии:голосовать за своего кандидата,и не голсова ть. |
|
|
|
|
|
||||||||
Будем искать симметричное равновесие в смешанных стратегиях,в котором вероятность, |
|
||||||||||||
что каждый избиратель проголосует,равна p.Обозначим за |
Pw(1, p) вероятность того,что по- |
|
|||||||||||
беду одержит кандидат A при условии,что один избиратель из первой группы проголосо вал,а |
|
||||||||||||
все остальные избиратели проголосовали с вероятностью p.Пусть Pw(0, p) — вероятость победы |
|
||||||||||||
кандидата A при условии,что один избиратель из первой группы не проголо совал,а все осталь- |
|
||||||||||||
ные проголосовали с вероятностью p.Таким образом,выигрыш избирателя равен |
Pw(1, p) − c |
|
|||||||||||
если он голосует,и pw(0, p),если он не голосует.В силу Леммы6в равновесии мы обязаны |
|
||||||||||||
иметь |
|
Pw(1, p) − c = Pw(0, p). |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
(3.16) |
|
||||
Вероятности Pw(1, p) и Pw(0, p) задаются следующими комбинаторными формулами: |
|
||||||||||||
Pw(1, p) = |
N−1 |
|
i |
|
|
+ |
1 N−1 |
CiN−1CiN+1p2i+1(1 − p)2N−2i−2 |
, |
||||
i=0 |
/CiN−1pi(1 − p)N−i−1 j=0 CjN pj(1 − p)N−j0 |
2 i=0 |
|||||||||||
|
( |
/CiN−1pi(1 − p)N−i−1 |
( |
|
0 |
|
|
( |
, |
|
|
|
- |
Pw(0, p) = |
N−1 |
i−1 |
|
+ |
1 N−1 |
CiN−1CiN p2i(1 − p)2N−2i−1(3..17) |
|||||||
i=1 |
j=0 CjN pj(1 − p)N−j |
2 i=0 |
|||||||||||
|
( |
|
( |
|
|
|
( |
, |
|
|
- |
|
|
Можно показать,что для любого |
c < |
1 ,при достаточно большом |
N уравнение(3.16)име- |
|
|||||||||
ет два решения,причем при увеличении |
2 |
|
|
|
|
|
|
|
|
|
|||
N одно решение приближается к нулю,другое — к |
|
||||||||||||
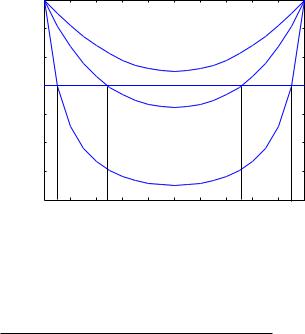
единице.На рисунке3.2показаны решения для c = 0.35 и различных N:
|
0.5 |
|
|
|
|
|
|
|
|
|
c |
0.45 |
|
|
|
|
|
|
|
|
|
(0, p), |
0.4 |
|
|
|
N = 2 |
|
|
|
|
|
w |
|
|
|
|
|
|
|
|
|
|
− P |
0.35 |
|
|
|
|
|
|
|
|
|
(1, p) |
0.3 |
|
|
|
N = 3 |
|
|
|
|
|
w |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
0.25 |
|
|
|
|
|
|
|
|
|
|
0.2 |
|
|
|
N = 10 |
|
|
|
|
|
|
0 |
p2−0.1 |
0.2 p1− 0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
p1+0.8 |
0.9 |
p2+ 1 |
Рис. 3.2:Решение уравнения(3.16)для c = 0.35 и разных N.
Получается,что существует два симметричных смешанных рав новесия:с высокой и с низкой явкой.В данном примере,для c = 0.35 и N = 2 равновесий нет,для N = 3 существуют два
3Первая постановка была рассмотрена Полфри и Розенталем(19 83),вторая — Полфри и Розенталем(1985).
3.1.БАЙЕСОВЫ ИГРЫ |
115 |
равновесия — p−1 и p+1 , для N = 10 — p−2 и p+2 .Наличие равновесия с высокой явкой интуитивно понятно:если избиратель знает,что остальные избиратели п очти наверняка проголосуют,и если две группы избирателей примерно одинаковы по размерам,то е го голос с большой вероятностью может стать решающим.Получается,что при помощи теоретико -игрового анализа мы нашли объяснение «парадоксу голосования».
Однако,к сожалению,эти выводы рушатся,если мы предположи м,что издержки избирателей ci есть их частная информация.Предположим,что у каждого изби рателя ci — это случайная величина,распределенная на [0, 1] с распределением F (·).Стратегией избирателя теперь будет его решение — голосовать или нет — в зависимости от его издержек ci.Попробуем найти для этой игры симметричное равновесие — то есть равновесие,в котором у всех избирателей одинаковые стратегии — голосовать,если издержки н е больше некоторой пороговой величины c¯.
Посмотрим,каким условиям должно удовлетворять это равнов есие.Во-первых,вероятность того,что отдельно взятый избиратель проголосует,должна б ыть равна вероятности,что его издержки не больше пороговых:
p = F (¯c). |
(3.18) |
Во-вторых,избирателю с издержками голосования,равными п ороговым,должно быть все равно,голосовать или нет:
Pw(1, p) − c¯ = Pw(0, p). |
(3.19) |
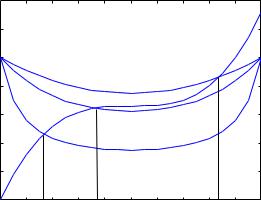
Решение этих двух уравнених изображено на рисунке3.3.
|
0.7 |
|
|
|
|
|
|
|
|
|
|
0.6 |
|
|
|
|
|
|
|
F −1(p) |
|
), c¯ |
|
|
|
|
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
|
|
|
|
(0, p |
|
|
|
|
|
N = 2 |
|
|
|
|
w 0.4 |
|
|
|
|
|
|
|
|
|
|
p) − P |
0.3 |
|
|
|
|
N = 3 |
|
|
|
|
(1, |
|
|
|
|
|
|
|
|
|
|
w |
|
|
|
|
|
|
|
|
|
|
P |
0.2 |
|
|
|
|
|
|
|
|
|
|
0.1 |
|
|
|
|
N = 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
0.1 |
p30.2 |
0.3 |
p20.4 |
0.5 |
0.6 |
0.7 |
0.8 p1 0.9 |
1 |
Рис. 3.3:Решение системы уравнений(3.18), (3.19)для разн ых N.
Можно доказать,что для любой функции распределения F (·) существует хотя бы одно симметричное равновесие при N ≥ 2.Также можно доказать,что при достаточно большом N равновесие одно,причем при N → ∞ мы имеем c¯ → 0 и p → 0,то есть голосуют только избиратели со все более низкими издержками,и доля активных избирателей стремится к нулю.
Тем не менее,теория дает нам несколько эмпирически проверя емых гипотез.Во-первой, явка должна быть выше при маленьком размере элетрората,так как это влияет на вероятность того,что голос избирателя окажется ключевым.Во-вто рых(и по той же причине)явка должна быть выше,если у одного из кандидатов нет явного преи мущества.Явка должна быть
меньше,если высоки издержки голосования(например,если е |
сть правила регистрации изби- |
рателей)и выше в том случае,если голосование обязательно( |
в некоторых странах гражданин, |
не проголосовавший на выборах,платит штраф).Наконец,ког |
да дело касается парламентских |

116 |
ГЛАВА3.СТАТИЧЕСКИЕ ИГРЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ |
выборов,явка должна быть выше в странах с пропорциональной системой.Все эти выводы находят эмпирическое подтверждение.4
3.1.2Теорема об очищении смешанных равновесий
Как мы заметили в1-й главе,существует определенная пробле ма интерпретации смешанных равновесий в играх с полной информацией.Почему игроки буду т принимать случайные решения?Ведь в любом равновесии в смешанных стратегиях выигр ыш каждого игрока от реализации каждой из его чистых стратегий одинаков.Равновеси е требует,чтобы каждый игрок смешивал свои чистые стратегии в определенной пропорции;о тклонение от этой пропорции сделает этого игрока уязвимым для действий других игроков.Одн ако проблема состоит в том,что порой бывает трудно придумать пример реалистичного поведения,в котором чистые стратегии сознательно смешивались бы.
Харшаньи(1973)доказал,что практически в любой игре с полн ой информацией равновесие в смешанных стратегиях можно рассматривать как предельный случай равновесия в чистых стратегиях в некоторой последовательности игр с неполной информацией.Действительно, предположим,что в некоторой игре выигрыш игрока i при выборе чистой стратегии si явля-
ется(с точки зрения второго игрока)случайной величиной;т |
|
огда любая чистая стратегия(то |
|||||||||||||
есть решение,что выбрать — X или Y ,в зависимости от типа)покажется второму игроку как |
|||||||||||||||
реализация некоторой смешанной стратегии. |
|
|
|
|
|
|
|
|
|
||||||
|
|
Формально,пусть G = I, A, u |
— конечная игра в нормальной форме.Определим для |
||||||||||||
|
|
ai |
|
|
|
промежутке |
[ |
|
1, 1] с положитель- |
||||||
каждой ai Ai случайную величину ti ,распределенную на |
− |
||||||||||||||
ai |
|
|
|
ai |
)ai Ai |
||||||||||
ной,непрерывно дифференцируемой функцией плотности f |
|
(·).Обозначим за |
ti = (ti |
||||||||||||
T |
i |
= [ |
1, 1]|Ai| тип игрока i,за T |
= |
N T |
i |
— множество типов игроков.Тогда функция |
||||||||
|
|
−N |
|
×i=1 |
|
|
|
|
|
|
|
|
|||
f(t) = |
i=1 fi(ti) задает плотность на множестве типов T . |
|
|
|
|
|
|
|
|||||||
|
|
Для1каждого ϵ > 0 рассмотрим игру с неполной информацией G˜(ϵ),в которой выигрыш |
|||||||||||||
игрока i при собственном профиле действий ai Ai,профиле действий остальных игроков a−i A−i,и собственном типе ti равен
uˆ |
i |
(a |
, a |
−i |
, t |
) = u |
(a |
, a |
−i |
) + ϵtai . |
(3.20) |
|
|
i |
|
i |
|
i |
i |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
˜ |
— профиль стратегий |
Как будут выглядеть равновесные стратегии в игре G(ϵ)?Пусть s |
||||||||||||
игроков.Пусть piai (s) — вероятность того,что игрок |
i выберет действие ai при условии,что ti |
|||||||||||
неизвестен.Ожидаемый выигрыш игрока j при реализации действия aj |
Aj будет |
|||||||||||
u˜i(ai, s−i, ti) = |
2t−i T−i |
ui(ai, s−i(t−i))df−i(t−i) + ϵtiai . |
(3.21) |
|||||||||
Следовательно,при данных s−i,почти при всех |
ti выигрыш игрока i максимизирован,если он |
|||||||||||
выберет какое-нибудь одно действие. |
|
|
|
|
|
|
|
|
|
|||
Пусть p(s) — вероятности того,что игроки будут реализовывать свои чис тые действия, при условии,что их типы неизвестны,а s — их стратегии.Результат,полученный Харшаньи, формулируется следующим образом.
Теорема11 Пусть G = I, A, u — игра в нормальной форме, a — равновесие(возможно,
смешанное)в этой игре.Тогда для каждого существует равновесие в игре ˜ ,такое,что
ϵ sϵ G(ϵ)
последовательность p(sϵ ) сходится к a при ϵ → 0 почти для всех игр G.
То есть почти в каждой игре с полной информацией,каждое равн овесие может быть представлено как предел последовательности равновесий в чистых стратегиях в играх с неполной
4Например,смотри работу Гейза(2006).

3.1.БАЙЕСОВЫ ИГРЫ |
117 |
||
информацией.Исключения составяляют случаи,подобные сле |
дующему: |
||
A |
B |
|
|
|
|
|
|
A 0, 0 |
0, 0 |
|
|
B0, 0 0, 0
Вэтой вырожденной игре любая пара вероятностей (p, q) будет являться равновесием.Однако рассмотрим игру с такими выигрышами:
|
A |
B |
|
A |
ϵt1, ϵ t2 |
ϵt1, 0 |
В этой игре,Игрок1получает ϵt1,если он играет AA,Игрок2получает ϵt2. |
B |
0, ϵ t2 |
0, 0 |
|
Получается,что p = P (ϵt1 ≥ 0), q = P (ϵt2 = 0).Если t1 и t2 распределены на [−1, 1] с распределениями F1(·), F2(·),то для всех ϵ > 0 мы получим p = 1 − F1(0), q = 1 − F2(0),то есть из всего континуума равновесий в исходной игре существует только одно,которое является пределом последовательности равновесий в видоизмененных играх.
Пример:Встреча в метро.
Рассмотрим,как можно реализовать приближение смешанных р авновесий чистыми на примере игры «встреча в метро» из Главы1.Напомним,что в исходной од нопериодной игре с полной информацией матрица выигрышей,определяющая функцию выиг рыша u, такова :
Игрок2
|
|
A |
B |
|
|
|
Игрок1 |
|
|
|
|
|
|
A |
(2, 2) |
(0, 0) |
|
|
|
|
|
B |
(0, 0) |
(1, 2) |
|
|
|
Рассмотрим такую игру с неполной информацией.Пусть ϵ > 0.Выигрыш игрока |
||||||
симости от его действий ai и действий другого игрока a−i,равен |
||||||
|
|
|
u˜i(ai, a−i) = |
$ ui(B, a−i), |
ai = B, |
|
|
|
|
|
|
ui(A, a−i) + ϵti, ai = A |
|
i,в зави-
(3.22)
где величины t1, t2 независимо распределены на [−1, 1].Найдем равновесие в этой игре.
Пусть p1, p2 — вероятности того,что игроки1и2будут реализовывать дейс |
твие A. При |
|
данном значении p2,игрок1сыграет a1 = A если и только если |
|
|
p2 · (2 + ϵt1) + (1 − p2)ϵt1 |
≥ p2 · 0 + (1 − p2) · 1. |
(3.23) |
Аналогично,игрок2сыграет a2 = A если и только если |
|
|
p1 · (2 + ϵt2) + (1 − p1)ϵt2 |
≥ p1 · 0 + (1 − p1) · 2. |
(3.24) |
Можно переписать эти условия как условия на t1 и t2:
ϵt1 |
≥ |
1 − 3p2, |
(3.25) |
ϵt2 |
≥ |
2 − 4p1. |
(3.26) |
Учитывая наши предположения о распределении величин t1 и t2,можно вывести зависимость p1,соотвествующую наилучшей реакции первого игрока на страт егию второго игрока,дающую вероятность p2, и наоборот :
|
|
|
≥ |
|
− |
|
0 |
|
1 3p2 |
|
p2 ≤ 1−3 ϵ |
|
|
|
|
|
|
|||||
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
p1(p2) |
= |
P (ϵt1 |
|
1 |
|
|
1 |
|
− |
, |
p2 |
|
3 |
|
, |
, 1+ϵ ) |
(3.27) |
|||||
|
|
3p2) = |
1 |
|
p2 |
|
(1−ϵ |
|||||||||||||||
|
|
|
|
|
|
|
2 |
|
2ϵ |
|
|
≥ |
3 |
|
|
3 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
0 |
|
|
|
p1 |
|
2−4 |
ϵ |
|
|
|
|
|
|
|||
|
|
|
≥ |
|
− |
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p2(p1) |
= |
P (ϵt2 |
|
2 |
|
|
1 |
|
1−2p1 |
, |
p1 |
≤ |
4 |
|
. |
, 2+ϵ ) |
(3.28) |
|||||
|
|
4p1) = |
1 |
|
p1 |
(2−ϵ |
||||||||||||||||
|
|
|
|
|
|
|
2 |
|
ϵ |
|
|
≥ |
4 |
|
|
4 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
118 |
|
|
|
ГЛАВА3.СТАТИЧЕСКИЕ ИГРЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ |
|||||||||||||||||
При ϵ < |
√2,у этой системы есть три решения.Во-первых,это |
(p |
, p ) = (0, 0). Во - вторых , |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
(p1, p2) = (1, 1).В-третьих, |
p1 и p2 являются решениями уравнений |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
p |
1 |
= |
1 |
− |
1 − 3p2 |
|
|
|
|
|
(3.29) |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2ϵ |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
p |
2 |
= |
1 |
− |
1 − 2p1 , |
|
|
|
|
|
(3.30) |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
ϵ |
|
|
|
|
|
|
||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
= |
|
23 + 4ϵ − ϵ22 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
3 −2 |
ϵ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
p |
= |
1 − ϵ2 . |
|
|
|
|
|
(3.31) |
||||
|
|
|
|
|
|
|
|
|
|
2 |
|
3 − ϵ2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
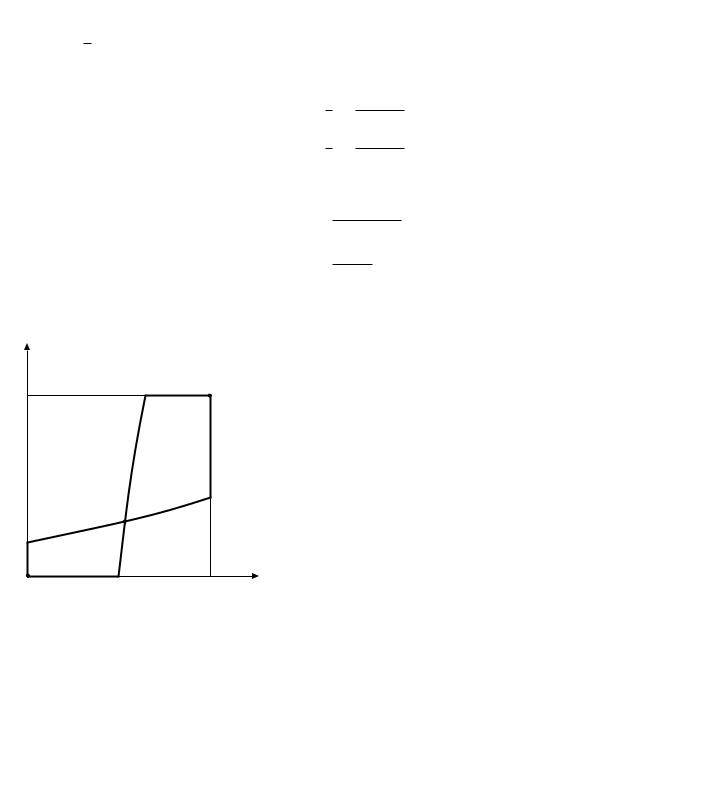
Каждое из трех решений соответствует одному равновесию в чистых стратегиях в байесовой |
|||||||||||||||||||||
игре3.4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p2(p1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
p1 |
(p2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
p1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.4:Равновесия в чистых стратегиях в байесовой игре. |
|
|
|
|
|||||||||||||||
В равновесии (p1, p2) = (0, 0),оба игрока всегда выбирают |
(B, B).В равновесии |
(p1, p2) = |
|||||||||||||||||||
(1, 1), они выбирают (A, A).В равновесии,определенном системой(3.30),стратегии вы |
бираются |
||||||||||||||||||||
исходя из(3.26),при |
p |
1 |
= p |
, p |
2 |
= p .При этом решение системы(3.30)при |
ϵ |
→ |
0 сходится к |
||||||||||||
|
1 |
1 |
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
(p1, p2) = (2 , |
3 ) — равновесие в смешанных стратегиях в исходной игре с совершенной инфор- |
||||||||||||||||||||
мацией.Таким образом,при снижении степени неполноты инфо |
рмации ϵ чистые стратегии в |
||||||||||||||||||||
игре с неполной информацией все больше и больше приближают смешанное равновесие в игре |
|||||||||||||||||||||
с полной информацией. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3.1.3Примеры
Производство общественного блага
Рассмотрим задачу производства общественного блага двумя лицами.Предположим,что для
производства блага достаточно,чтобы любой из двух игроков |
принял решение участвовать в |
||||
его производстве.Матрица выигрышей игроков,в зависимост |
и от их действий,будет такой: |
||||
|
|
Игрок2 |
|
|
|
Игрок1 |
|
Производить |
Не производить |
||
|
|
|
|
|
|
Производить |
1 − c1, 1 − c2 |
1 − c1, 1 |
|
|
|
|
Не производить |
1, 1 − c2 |
0, 0 |
|
|

3.1.БАЙЕСОВЫ ИГРЫ |
119 |
Пусть издержки игроков c1, c2 являются частной информацией.Предположим,что издержки игрока i равномерно распределены на промежетке [ci, c¯i], i = 1, 2, 0 ≤ ci < c¯i ≤ 1.Найдем байесово равновесие в этой игре.
Рассмотрим,как выглядят равновесные стратегии для обоих и гроков.Пусть вероятность того,что игрок i станет участвовать в производстве блага,равна pi.Выигрыш игрока i равен 1 − ci если он производит благо,и p−i,если он не производит.Следовательно,вероятность pi определяется как
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
pi = P (1 |
− |
ci |
≥ |
p−i) = P (ci |
≤ |
1 |
− |
p−i) = |
1−c¯i−ic−i |
|
i |
, |
|
|
|
|
|
|
|
1, − |
c |
|
|
||||
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
Система уравнений |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
p1 = p1(p2), p2 = p2(p1) |
||||||||
p−i p−i p−i
≥ 1 − ci
(1 − c¯i, 1 − ci)
≤ 1 − c¯i
(3.32)
(3.33)
имеет три решения: (p1, p2) = (1, 0), (p1, p2) = (0, 1), и (p1, p2),удовлетворяющие условиям
p1 |
= |
1 |
− p2 |
− c1 |
|
(3.34) |
|
||||||
|
|
|
c¯1 − c1 |
|
||
p2 |
= |
1 |
− p1 |
− c2 |
. |
(3.35) |
|
||||||
|
|
|
c¯2 − c2 |
|
||
Решением этой системы будет
p1 |
= |
1 − c¯2 + c1(¯c2 − c2) |
|
||
|
|
1 − (¯c1 |
− c1)(¯c2 |
− c2) |
|
p2 |
= |
1 − c¯1 + c2(¯c1 − c1) |
. |
||
|
|
1 − (¯c1 − c1)(¯c2 |
− c2) |
||
Полученные вероятности соответствуют следующим равновесным стратегиям:
1.Игрок1всегда производит общественное благо,игрок2ник |
огда не производит |
||||
2.Игрок2всегда производит общественное благо,игрок1ник |
огда не производит |
||||
3.Игрок i производит общественное благо,если и только если |
|
||||
ci |
≤ |
c˜i = |
c¯i − c¯−i(¯ci − ci) |
. |
|
|
|
1 − (¯c1 − c1)(¯c2 − c2) |
|
||
(3.36)
(3.37)
(3.38)
В этой задаче существует единственное равновесие,при кото ром p1, p2 (0, 1),то есть оба игрока с положительной вероятностью выбирают каждое из двух своих действий.Это — следствия нашего предположения о том,что c1 и c2 распределены равномерно.При других распределениях этих величин возможно несколько равновесий.
Двойной аукцион |
|
|
|
|
|
|
|
|
||||
В т´орговой задаче Нэша (см.задачу26в первой главе)продавец и покупатель одновре |
менно |
|||||||||||
|
|
|
|
5 |
|
|
|
|
|
|
|
|
называют цены,по которой они хотят купить/продать товар.П |
усть p1 — цена,которую назвал |
|||||||||||
продавец, p |
|
— цена,названная покупателем.В случае,когда p |
1 ≤ |
p |
,происходит обмен по цене |
|||||||
|
p1+p2 |
|
2 |
|
|
|
|
2 |
|
|
||
p = |
|
;выигрыши продавца и покупателя составят |
|
|
|
|
|
|
||||
2 |
|
|
|
|
|
|
||||||
|
|
|
|
U1 = |
p1 + p2 |
− c и U2 = v − |
p1 + p2 |
. |
|
|
(3.39) |
|
|
|
|
|
2 |
2 |
|
|
|
||||

120 |
ГЛАВА3.СТАТИЧЕСКИЕ ИГРЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ |
При p1 > p2,торговли не происходит,и выигрыши обоих сторон равны нулю . |
|
|
Четерджи и Сэмюэльсон(1983)проанализировали вариант это й задачи для того случая, |
когда v и c — частная информация.Предположим,что эти величины равном ерно и независимо распределены на [0, 1].Стратегиями продавца и покупателя будут зависимости их за явок от
оценок: p1(c) и p2(v).Ожидаемый выигрыш продавца при данном |
c и p1 равен |
|
|||||
U˜1 = P (p1(c) ≤ p2) ) |
1 |
2| |
|
≤ |
|
− c*. |
(3.40) |
|
p |
(c) + E(p2 |
p1(c) |
|
p2) |
|
|
Соответственно,для любого c [0, 1], p1(c) должно максимизировать U1.Аналогично,для любого v [0, 1], p2(v) должно максимизировать
|
|
|
|
U˜2 = P (p1 ≤ p2(v)) )v − |
|
| |
|
≤ |
2 |
|
|
2 |
|
*. |
|
|
|
|
|
|
(3.41) |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
E(p1 |
|
p1 |
|
p2 |
(v)) + p |
|
(v) |
|
|
|
|
|
|
|
|
|
|
|
|||
Можно убедиться,что p1(c) и p2(v) будут возрастающими функциями.Действительно,возьмем |
|
|||||||||||||||||||||||||||||||||
два уровня издержек: c′ и c′′.Тогда,исходя из оптимальности |
p1(c),мы должны иметь |
|
|
|
|
|
|
|||||||||||||||||||||||||||
P (p1(c′) ≤ p2) ) |
p1(c′) + E(p2 |
p1(c′) |
|
|
p2) |
− c′* ≥ P (p1(c′′) ≤ p2) ) |
p |
(c′′) + E(p2 |
p1(c′′) |
|
|
p |
) |
− c′* |
||||||||||||||||||||
|
|
|
2| |
|
|
≤ |
|
|
|
1 |
|
|
2| |
|
|
≤ |
|
2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.42) |
|
||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P (p1(c′′) ≤ p2) ) |
p |
(c′′) + E(p2 |
p1(c′′) |
|
|
p2) |
− c′′* ≥ P (p1(c′) ≤ p2) ) |
p1(c′) + E(p2 |
p1(c′′) |
|
|
p2) |
|
*, |
||||||||||||||||||||
1 |
|
2| |
|
|
≤ |
|
|
|
|
|
2| |
|
|
≤ |
|
|
|
− c′′ |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.43) |
|
||
что дает нам |
|
|
|
(c′′ − c′)(P (p1(c′) ≤ p2) − P (p1(c′′) ≤ p2)) ≥ 0, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(3.44) |
|
||||||||||||||||||||||
то есть p1(c′′) ≥ p1(c′) если c′′ ≥ c′. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Сразу отметим,что в этой игре много равновесий.Существует |
,например,вырожденное |
|
||||||||||||||||||||||||||||||||
равновесие,в котором |
p1 = 1 и p2 = 0.Легко заметить,что и |
p1 = 1, и p2 = 0 являются доста- |
|
|||||||||||||||||||||||||||||||
точными условиями для того,чтобы обмена никогда не происхо дило(и оба игрока получали |
|
|||||||||||||||||||||||||||||||||
нулевой выигрыш).Есть и такое равновесие: |
|
|
|
$ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
$ |
|
1, |
|
c > p˜ |
|
|
|
0, |
v < p˜ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
p1 = |
|
|
p,˜ |
|
c |
≤ p˜ и p2 |
= |
|
p,˜ |
v |
≥ p˜ |
|
|
|
|
|
|
|
|
|
|
(3.45) |
|
|||||||
для любого p˜ (0, 1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Попробуем ограничить наше внимание линейными стратегиями,когда заявляемая цена яв- |
|
|||||||||||||||||||||||||||||||||
ляется линейной функцией от v или c: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
p1 |
= α1 + β1c, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.46) |
|
|||||||
|
|
|
|
|
|
|
|
|
|
p2 |
= α2 + β2v. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.47) |
|
|||||||
Таким образом,стратегия игрока i = 1, 2 сводится к параметрам (αi, βi).Найдем ожидаемые полезности покупателя и продавца в зависимости от их стратегий.
Пусть покупатель играет линейную стратегию p2 = α2 + β2v.Мы имеем
|
|
|
/ |
p1 + |
p1+α2+β2 |
|
0 |
|
U˜ |
1 |
= |
α2 + β2 − p1 |
|
|
− |
c , |
(3.48) |
|
|
β2 |
2 |
|
|
|||
5Эта задача разбиралась также у Гиббонса(1992)и Тироля и Фад енберга(1991).
