
game_theory
.pdf1.2. CМЕШАННЫЕ СТРАТЕГИИ И СУЩЕСТВОВАНИЕ РАВНОВЕСИЯ |
31 |
Большое число игроков
Для некоторых случаев смешанные равновесия в игре с небольшим числом игроков могут описывать равновесия в чистых стратегиях в тех случаях,когда и гроков на самом деле много. Рассмотрим,например,игру между безбилетником и контроле ром на странице20.Напомним, что в этой игре существует единственное равновесие в смешанных стратегиях,в котором каждый из двух игроков с равной вероятностью выбирает одно из двух действий(садиться в первый или во второй вагон поезда).Предположим,что и безбилетник ,и контролер могут играть только чистые стратегии,но безбилетников и контролеров много — скажем,несколько тысяч.Если одна половина контролеров идет в первый вагон поезда,а друг ая половина — во второй,то для безбилетника,столкнувшегося со случайно выбранным контр олером,эта ситуация эквивалентна встрече с контролером,играющим равновесную смешанную с тратегию.То же самое верно и для конторолера;с точки же зрения стороннего наблюдателя, и безбилетник,и контролер оба играют смешанные стратегии.Такая интерпретация удобна,н о не всегда уместна:иногда число игроков в моделируемой ситуации действительно мало(напри мер,если речь идет о международном конфликте),либо мы не имеем право предполагать,что игроки сталкиваются друг с другом впервые(«семейный спор»).
Смешанные стратегии как следствие ненаблюдаемой полезности игроков
Смешанные стратегии могут быть следствием того,что выигры ш игрока в зависимости от реализуемой им стратегии может быть известен ему одному.Расс мотрим пример на странице13. Маша и Андрей должны выбрать одно из двух мест встречи;если и х выборы совпадает,то каждый из них получает единичную полезность,если выборы не сов падеет,то полезность каждого равна нулю.В этой игре существует три равновесия:два — в чис тых стратегиях(каждое из которых соответствует одному из мест встречи),и одно — в сме шанных(в нем каждый из двух игроков выбирает одно из двух мест встречи с равной вероятностью).Как можно объяснить существование третьего равновесия?Предположим,что итог овая полезность Андрея от места встречи,которое он выбрал,зависит от ненаблюдаемых Машей вещей — например от того,с какой ноги Андрей встал сегодня утром.Если Андрей встал с ле вой ноги,то он будет отдавать предпочтение встрече у метро,если с правой — то встрече у теа тра.В таком случае,с точки зрения Маши он будет играть смешанную стратегию,а со своей с обственной точки зрения — чистую.Маша действует точно так же;оба игрока при этом пост упают рационально,но(с точки зрения стороннего наблюдателя)при этом действуют случа йным образом.Более подробно об этом примере и об играх с ненаблюдаемой полезностью мы будем говорить в третьей главе этой книги.
1.2.4Смешанное равновесие в антагонистической игре 2 × M
Важный подкласс игр составляют игры,в которых сумма выигры шей игроков одинакова,вне зависимости от профиля стратегий,выбираемого игроками.
Определение12 Игра G = I, S, u является игрой с постоянной суммой,если
N |
|
( |
(1.43) |
ui(s) = c |
|
i=1 |
|
для некоторого c и всех s S.Если N = 2,то такая игра называется |
антагонистической. |
Такие игры часто также называют играми с нулевой суммой.В да нном случае название
— это вопрос вкуса;примерами игр с нулевой суммой являются с алонные игры,игры типа
32 |
|
ГЛАВА1.СТАТИЧЕСКИЕ ИГРЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ |
|||||
uF |
|
|
|
|
uF |
|
|
|
|
|
|
0.9 |
|
|
|
0.8 |
|
|
|
|
0.8 |
CC |
|
|
|
|
|
|
|
||
|
|
|
|
0.7 |
|
|
0.7 |
0.6 |
Lob |
|
|
|
|
DL |
0.6 |
|
|
|
0.5 |
0.5 |
|
|
|
|
|
DL |
|
|
|||
|
|
|
|
|
|
||
0.2 |
CC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.5 |
2 |
1 |
q |
|
3 |
1 p |
|
3 |
|
4 |
||||
|
|
|
|
|
|
||
(a)Для смешанной стратегии Надаля |
q и разных (b)Для смешанной стратегии Федерера p и раз - |
||||||
чистых стратегиях Федерера |
|
|
|
ных чистых стратегий Надаля |
|
||
|
Рис. 1.6:Нахождение равновесия при трех чистых стратегиях |
у Федерера. |
|||||
«инспекция»,предвыборная борьба,заключение опционных к онтрактов на фондовом рынке. |
|||||||
Существование равновесия и многие другие результаты для этого класса игр были получены |
|||||||
великим математиком Джоном фон Нейманом(см.книгу фон Нейм ана и Моргенштерна, 1970). |
|||||||
Рассмотрим пример с игрой в теннис.Пусть в арсенале у Федере ра есть еще один удар: Lob |
|||||||
(«свеча»).Матрица игры теперь такая: |
|
|
|
||||
Надаль
DL CC
DL 0.5 0.8
Федерер CC 0.9 0.2
Lob 0.7 0.6
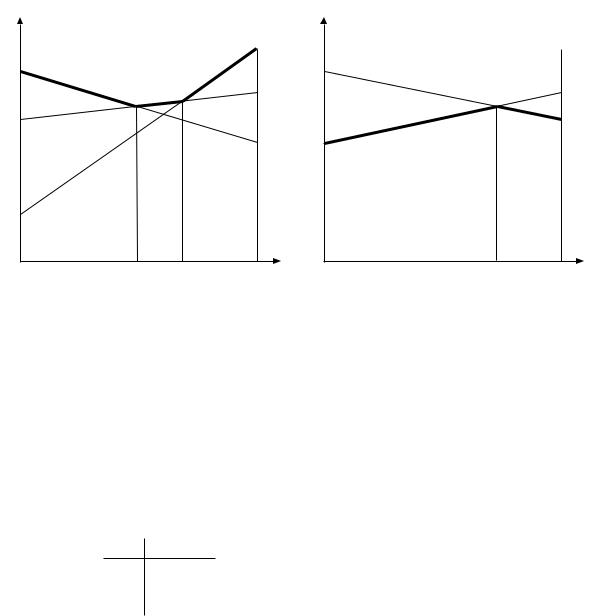
На рисунке1.6(a)показано,как выигрыш Федерера зависит от смешанной стратегии Надаля q для каждой из трех чистых стратегий Федерера,где q,как и раньше,есть вероятность того, что Надаль сыграет DL.
Жирная ломаная линия показывает максимальную полезность, которую может получить Федерер,в зависимости от стратегии Надаля q.По этому графику можно построить функцию реакции Федерера.Если q < 0.5,то Федерер играет DL,если q = 0.5 — то любую смесь DL и Lob,если q (0.5, 23 ), то Lob,если q = 23 — то смесь Lob и CC,если q > 23 — то CC.
Так как эта игра является антагонистической,то в равновеси и стратегия Надаля должна минимизировать максимальную полезность Федерера.Действ ительно,предположим,что в рав-
новесии q ̸= 0.5.Тогда(предполагая равновесие)выигрыш Федерера будет ма |
ксимальным для |
данного q.Но это означает,что Надаль может увеличить свой выигрыш,в |
ыбрав стратегию |
q = 0.5.Таким образом, q = 0.5.Нам остается найти пропорции,в которых Федерер играет DL и Lob.На рисунке1.6(b)показан выигрыш Федерера и Надаля в завис имости от p — вероятности,с которой Федерер играет Lob,при разных чистых стратегиях Надаля.Жирная линия
— минимальный выигрыш Федерера(и,соответственно,максим альный выигрыш Надаля)в зависимости от p.Из графика видно,что p = 34 .
Давайте немного изменим выигрыши игроков:

1.3.НЕПРЕРЫВНЫЕ ИГРЫ |
|
33 |
|
uF |
|
|
|
|
|
|
0.9 |
0.8 |
DL |
|
|
|
|
|
|
0.62 |
|
|
0.62 |
0.55 |
Lob |
|
0.55 |
|
|
0.5 |
|
0.2 |
CC |
|
|
|
|
|
|
|
0.6 |
1 |
q |
|
Рис. 1.7:Смешанная стратегия доминирует чистую стратегию |
||
|
|
Надаль |
||
|
|
|
DL |
CC |
|
|
|
|
|
Федерер |
DL |
|
0.5 |
0.8 |
CC |
|
0.9 |
0.2 |
|
|
|
|||
|
Lob |
|
0.55 |
0.55 |
Выигрыш Федерера в зависимости от q показан на рисунке1.7.
Как мы видим,Федерер не станет использовать стратегиюLobн и при каких q.Стратегия Lobне доминируется ни одной их двух других чистых стратегий ;однако она доминируется
некоторыми смешанными стратегиями — например,смесью из70 |
% DL и 30% CC,которая дает |
Федереру ожидаемый выигрыш0.62вне зависимости от стратег |
ии Надаля.Поэтому мы по- |
ступаем с ней,как и с любой другой доминируемой стратегией — |
вычеркиваем.Она не будет |
играться ни в одном равновесии,чистом или смешанном(см.за дачу20).
1.3Непрерывные игры
Теорема о существовании равновесия в смешанных стратегиях была доказана для конечных игр:мы предполагали,что у каждого игрока конечное число ст ратегий.Во многих играх,напротив,удобно считать,что множество стратегий не являетс я конечным или даже счетным. Например,в дуополии Курно стратегия каждой из двух фирм — ка кое-то неотрицательное действительное число.Это предположение облегчает нам ана лиз задачи,так как(предполагая дифференцируемость функуций полезности)мы можем нахо дить равновесия,анализируя локальные максимумы функций полезностей игроков.Дуополи я Курно соответствует следующему определению:
Определение13 Игра G = I, S, U является непрерывной игрой,если для всех i,множество стратегий Si является выпуклым подмножеством конечномерного Евклидового пространства Rdi ,а функция полезности ui(s) является непрерывной по s.
1.3.1Теоремы о существовании равновесия
Можем ли мы что-нибудь сказать о существовании равновесий в чистых и смешанных стратегиях в таких играх?Существуют несколько теорем,которые об означают необходимые условия существования равновесий в непрерывных играх.Определим т акое свойство функций:
34 |
ГЛАВА1.СТАТИЧЕСКИЕ ИГРЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ |
Определение14 Пусть X — подмножество конечномерного Евклидова пространства. Функция u : X → R является квазивогнутой если для всех u¯, множество {x|u(x) ≥ u¯} является выпуклым.
Лекго показать,что каждая вогнутая функция является квази вогнутой,но не наоборот. Также верно то,что каждая монотонная функция одной перемен ной является квазивогнутой (см.задачу8).
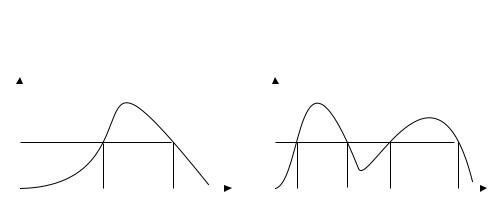
Примеры квазивогнутой и не квазивогнутой финкций приведены на рисунке1.8.
f(s) |
|
|
|
|
f(s) |
|
|
|
|
|
|
u¯ |
|
|
|
|
u¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
s |
||
|
(a)Квазивогнутая функция |
(b)Не квазивогнутая функция |
|||||||||
Рис. 1.8:Примеры квазивогнутости и ее отсутствия.
На рисунке1.8(a)функция удовлетворяет условиям:для данн ого u¯ (как и для любого другого)множество {s|u(s) ≥ u¯} (показанное на рисунке)является выпуклым.На рисунке1.8( b) условия квазивогнутости нарушаются:для данного u¯ множество {s|u(s) ≥ u¯} является объединением двух отрезков — то есть не выпуклым.
На свойство квазивогнутости опирается следующая теорема, доказанная Гликсбергом
(1952):
Теорема2 Рассмотрим непрерывную игру G,в которой множества стратегий Si являются компактными.Предположим,что для каждого игрока i функция полезности ui(si, s−i) является квази-вогнутой по si для всех s−i S−i.Тогда в игре I, S, u существует равновесие Нэша в чистых стратегиях.
Доказательство этой теоремы похоже на доказательство теоремы Нэша:мы показываем,что точечно-множественное отображение,построенное из функц ий реакции игроков,удовлетворяет условиям теоремы Какутани и имеет непрерывную точку.Более того,теорема о существовании смешанного равновесия в конечных играх является частным случаем этой теоремы.Действительно,смешанное расширение любой конечной игры является непрерывной игрой,удовлетворяющей условиям Теоремы2.
Квазивогнутость и непрерывность функций полезности является условиями,гарантирующими непрерывность функций реакции игроков.Посмотрим,чт о произойдет,если одно из этих условий будет нарушено.
Пример.
Пусть S1 = S2 = [0, 1],
u1(s1, s2) |
= |
max{s2 − s1, s1 − s2} |
(1.44) |
|||
u2(s1, s2) |
= |
−s22 + ) |
2 |
+ s1 |
*s2. |
|
|
|
|
1 |
|
|
|
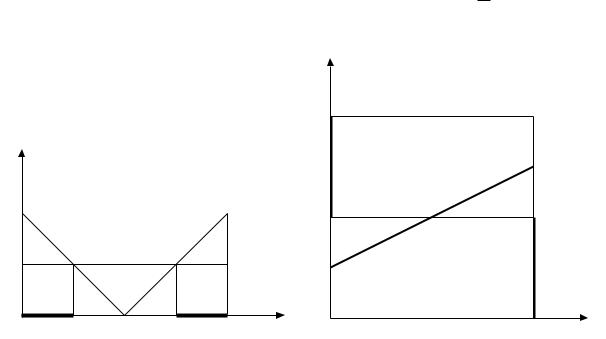
Обе функции полезности непрерывны по s1 и s2.Однако функция полезности первого игрока не является квазивогнутой:из рисунка1.9(a)видно,что мно жество значений s1, при которых u1 ≥ u¯,не является выпуклым.Функция реакции первого игрока не яв ляется непрерывной:
1.3.НЕПРЕРЫВНЫЕ ИГРЫ |
|
|
|
|
|
|
|
35 |
||
|
|
|
0, |
|
|
s2 > |
1 |
s2(s1) = 0.25 + s1 . |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
s1 |
(s2) = |
{ |
0, 1 |
} |
, |
s1 = 21 , |
(1.45) |
||
|
|
|
|
|
s2 < |
1 |
2 |
|
||
|
|
|
1, |
|
|
2 |
|
|
||
|
|
|
|
|
|
|
s2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
u1 |
|
|
|
|
|
|
|
s1 |
(s2) |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u¯ |
|
|
|
|
|
|
|
|
s2(s1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
s1 |
|
|
|
1 |
s1 |
|
|
2 |
|
|
|
|
|||||
(a)Функция полезности игрока1не является |
|
|
(b)Функции реакции игроков не пересекаются |
|||||||
квазивогнутой( s2 |
= 1 ) |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
Рис. 1.9:Пример отсутствия равновесия в непрерывной игре. |
|
||||||||
Графики функций реакции не пересекаются(рисунок1.9(b)), следовательно,равновесия в чистых стратегиях не существует.
Можем ли мы рассчитывать на существование равновесия Нэша в смешанных стратегиях в бесконечных играх?Оказывается,что не всегда:
Теорема3 Рассмотрим игру,в которой множества стратегий Si являются выпуклыми и компактными подмножествами конечномерных Евклидовых пространств Rdi .Предположим,что для каждого игрока i функция полезности ui(si, s−i) является непрерывной по s = (si, s−i). Тогда в игре I, S, u существует равновесие Нэша в смешанных стратегиях.
Доказательство этой теоремы технически более сложно,чем д оказательства предыдущей теоремы и теоремы Нэша,ибо множество смешанных стратегий в непрерывной игре является бесконечномерным.Здесь необходим более сильный результа т,чем теорема Какутани;доказательство(или даже формулировка)которого выходят за рам ки этой книги.Однако можно рассуждать(весьма приблизительно),что нарушение непрер ывности функций полезности по чистым стратегиям ведет к нарушению непрерывности по смешанным стратегиям.
1.3.2Примеры
Борьба за ренту
Две фирмы соревнуются за право построить магазин на центральной площади города.Для того,чтобы получить контракт,необходимо потратить некот орую сумму денег на лоббирование органов власти.Успех не гарантирован — но чем больше денег б удет потрачено каждой из фирм,тем больше вероятность того,что именно эта фирма полу чит контракт.Пусть прибыль,

36 |
ГЛАВА1.СТАТИЧЕСКИЕ ИГРЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ |
которую может приносить магазин,равна R.Предположим,что вероятность того,что фирма i = 1, 2 получит контракт,равна
rγ
Pi = γ i γ , (1.46) r1 + r2
где ri — количество средств,потраченное фирмой i, γ ≥ 0 — параметр,отражающий эффективность лоббирования.Чем выше γ,тем больше преимущество фирмы,затратившей на лоббирование больше средств.Действительно,рассмотрим два к райних случая.Если γ = 0, то вероятность получить контракт всегда равна 12 ,вне зависимости от объема средств,потраченных на лоббирование.Если же γ = ∞,то контракт с вероятностью1достается фирме,которая затратила больше средств на лоббирование.
Получается,что функция полезности фирмы i = 1, 2 будет
riγ |
(1.47) |
ui(r1, r2) = Rr1γ + r2γ − ri, |
где ri [0, ∞) — стратегия фирмы i.
Вболее общем случае мы рассматриваем задачу состязательного распределения ресурса,
вкоторой вероятность приобретения ресурса одной из сторон является функцией от усилий, затраченных в борьбе за этот ресурс.Большой объем литерату ры в области моделирования состязаний восходит к известным работам Таллока(1967),Кр югер(1974)и Познера(1975).
Лоббирование,коррупция,патентные гонки,спортивные сос |
тязания и войны — все это яв- |
ляется примером состязательных процессов.В таких играх,в |
ероятность успеха возрастает с |
увеличением затрат,однако сами затраты являются невозвра тными,и не возмещаются игроку в случае проигрыша.
Функции полезности являются дифференцируемыми по r1 и r2.Соответственно,если (r1, r2)
— равновесие,то в нем должны выполняться необходимые услов ия первого порядка
∂ui |
= |
0 |
при ri > 0 |
|
∂ri |
||||
|
|
|
||
∂ui |
≤ |
0 |
при ri = 0 |
|
∂ri |
для i = 1, 2.Второе условие было записано,ибо мы рассматриваем задачу зации,при ri ≥ 0.
Мы имеем
∂ui |
|
γrγ−1rγ |
|
|
= R |
i −i |
− 1 |
∂ri |
(r1γ + r2γ)2 |
для i = 1, 2.Условия первого порядка дают нам единственное решение
r1 = r2 = γ4R.
(1.48)
условной максими-
(1.49)
(1.50)
Легко проверить,что условия максимума второго порядка в эт ой точке будут выполнены.Однако (r1, r2) = (γ4R , γ4R ) будет равновесием Нэша только если γ ≤ 2.В обратном случае равновесия
не существует,так как u1(r1, r2) = R2 − γ4R < 0 = u1(0, r2) (при том,что (r1, r2) = (γ4R , γ4R ) является необходимым условием равновесия).Если γ > 0, то (r1, r2) является всего лишь локальным
равновесием — то есть в этой точке функция полезности каждого игрока имеет локальный (но не обязательно глобальный)максимумум на множестве стр атегий этого игрока.При этом функции полезности являются квазивогнутыми только при γ [0, 1]. При γ (1, 2],полезности не являются квазивогнутыми(рисунок1.10).
Тем не менее,равновесие существует:квазивогнутость функ ций полезности является достаточным(но не необходимым)условием существования равнове сия.

1.3.НЕПРЕРЫВНЫЕ ИГРЫ |
|
|
|
|
|
37 |
||||||
|
|
|
|
|
|
u1 |
|
|
|
|
|
|
u1 |
|
|
|
u1 |
|
|
γR |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
γR |
r1 |
|
γR |
r1 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|||||
4 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
(a) 0 < γ ≤ 1 |
|
|
|
(b) 1 < γ ≤ 2 |
|
|
(c) γ > 2 |
|
|
|
|
Рис. 1.10:Функция полезности игрока1в игре «борьба за рент |
у»,при условии,что r2 |
= |
Rγ |
. |
||||||||
|
||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
Что же происходит?При борьбе за приз оба игрока тратят значи тельные ресурсы.Например при γ = 1,что соответствует обычной лотерее,общий объем затрачива емых ресурсов будет равен половине от стоимости ресурса.Можно показать(см.зада чу25),что при увеличении числа игроков общий объем затрат на лоббирование стремится к ценности самого приза,за который ведется борьба( R в нашей модели).Также объем ресурсов,затрачиваемых на сос тязательную деятельность,возрастает при улучшении технологии лоббир ования(величины γ).Все это — свидетельство того,что при отсутствии прозрачных механиз мов распределения лицензий на ведение многих прибыльных видов экономической деятельности(импортные квоты,строительство в условиях ограниченного предложения земли и т.д.)общество несет значительные(и часто невидимые стороннему наблюдателю)потери.
Конкуренция на рынке с горизонтально дифференцированным товаром
Вот пример,восходящий к классической работе Гарольда Хоте ллинга(1929).На южном морском курорте есть пляж длиной1километр.На пляже расположе ны отдыхающие.Будем считать,что отдыхающих — континуум,а их общая масса равна един ице.Будем считать,что отдыхающие распределены равномерно:то есть для каждого x [0, 1] доля отдыхающих с координатами v ≤ x равна x.На пляже действуют два продавца с мороженым.Стратегия каж дого продавца i — координата si [0, 1] расположения тележки,с которой он продает мороженое. Цена у обоих продавцов одинаковая и не зависит от их местоположения.
Предположим,что каждый покупатель в течение дня купит ровн о один стакан мороженого. При этом покупатель купит морожение у того продавца,чья тел ежка расположена ближе.В том случае,если продавцы равноудалены от покупателя,он с равн ой вероятностью выберет каждого из двух продавцов.Пусть выигрыш продавца равен доле покупа телей,которые приобрели у него
мороженое.Таким образом,выигрыш продавца |
i = 1, 2 равен |
|
||||||
|
|
s1+2 s2 , |
si < s−i |
|||||
Ui(s1, s2) = |
21 , |
|
s1+s2 |
s1 = s2 |
(1.51) |
|||
|
|
1 |
− |
|
|
, si > s |
|
i, |
где −i — индекс другого продавца. |
2 |
|
||||||
|
|
|
|
|
− |
|
||
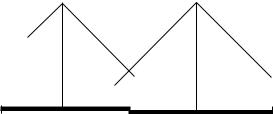
Распределение покупателей между продавцами показано на рисунке1.11. |
||||||||
На этом рисунке показаны графики двух функций:полезность п окупателя с данным рас- |
||||||||
положением при покупке у первого и второго продавцов.Покуп атель с расположением |
s1 |
+s2 |
|
|||||||||||
|
|
2 |
||||||||||||
безразличен между двумя продавцами;при s1 < s2,все покупатели с расположением v < |
s1 |
+s2 |
|
|||||||||||
|
2 |
|||||||||||||
приобретут мороженое у продавца1,все покупатели с v > |
s1+s2 |
— у продавца 2. |
|
|||||||||||
|
|
|||||||||||||
|
|
|
||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
Легко проверить,что в этой игре существует единственное ра вновесие,в котором s1 = |
||||||||||||
s2 |
= 21 .Действительно,в равновесии мы не можем иметь |
s1 ̸= s2.Если,без потери общности, |
||||||||||||
s |
|
< s |
,то любой продавец |
i может увеличить свой выигрыш,взяв s′ |
(s |
, s |
).Следовательно, |
|||||||
|
1 |
2 |
|
1 |
|
|
i |
1 |
2 |
|
|
|
|
|
в равновесии s1 = s2 = s.Но если s > 2 ,то любой продавец сможет увеличить свой выигрыш,
38 |
ГЛАВА1.СТАТИЧЕСКИЕ ИГРЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ |
0 |
s1 |
+s2 |
s2 |
1 |
s1 |
2 |
|||
|
|
|
|
Рис. 1.11:Горизонтальная конкуренция и доли рынка продавц ов.
взяв s′i (s, 1 −s).Таким образом,мы должны ожидать,что тележки продавцов ра сположатся рядом,причем их положение будет совпадать с расположением медианного покупателя — то есть такого,что равное число покупателей располагается сп рава и слева от него.
История с двумя продавцами мороженого — хорошая метафора для рынка с горизонтально дифференцируемым товаром.Например,главный параметр,по которому отличаются друг от друга современные пассажирские самолеты — это соотношение стоимости самолета и удельных издержек перевозки одного пассажира.С одного конца спектр а мы имеем небольшие региональные самолеты;с другого — вместительные и дорогие авиал айнеры с низкими эксплуатационными издержками в расчете на одного пассажира.Авиакомпа нии — потребители самолетов
— тоже отличаются друг от друга отчасти по тому,какие самоле ты им нужны.Например,одни компании обслуживают большое число маршрутов с небольшим пассажиропотоком,другие — более загруженные маршруты.
Модель предвыборной конкуренции
Начиная с известной книги американского политолога Энтони Даунса(1957),модель горизонтальной конкурении используется при моделировании поведения политических партий или кандидатов на выборах.Предположим,что в некоторой стране президентский пост оспаривают два кандидата.Стратегией каждого кандидата является его п редвыборная программа.Будем считать,что программа описывается одним параметром — степ енью ее левизны или правизны. Левая политика означает высокие налоги,значительные затр аты на производство общественных благ и социальные программы(такие,как пенсии или помощ ь малоимущим)за счет налогов,собранных с более состоятельных граждан.Правая пол итика — низкие налоги и малые затраты на социальную сферу.Пусть s1, s2 [0, 1] — политические программы кандидатов,где s = 0 — крайне левая программа, s = 1 — крайне правая .
Полезность кандидата равна доле голосов избирателей,полу ченных им на выборах.Пусть для каждого избирателя существует величина v [0, 1] — политическая программа,которая больше всего ему нравится,или его наилучшая альтернатива. Избиратели отличаются друг от друга своими предпочтениями относительно политических программ.Например,наилучшая альтернатива человека со средним достатком будет правее наилучшей альтернативы мало зарабатывающего пенсионера,но левее,чем наилучшая альтерн атива бизнесмена.Предположим, что наилучшие альтернативы избирателей равномерно распределены на [0, 1].
Будем считать,что избиратель v проголосует за кандидата1если |s1 −v| < |s2 −v| и проголосует за кандидата2если |s1 −v| ≥ |s2 −v|.В таком случае модель политической конкуренции между двумя кандидатами ничем не будет отличаться от конкуренции между двумя продавцами мороженого,рассмотренной в предыдущем примере.В рав новесии,оба кандидата станут центристами: s1 = s2 = 12 .В более общей постановке,если наилучшие альтернативы изб ирателей распределены на [0, 1] с функцией распределения F (·),то есть если доля избирателей с наилучшими альтернативами v ≤ x равна F (x),в равновесии предвыборные программы избирателей будут s1 = s2 = F −1(12 ) = vm.Программа vm является наилучшей альтернативой

1.3.НЕПРЕРЫВНЫЕ ИГРЫ |
39 |
медианного избирателя,то есть это такая альтернатива,что одна половина избирате лей имеет более левые взгляды,другая половина — более правые.
Модель предвыборной конкуренции с идеологическими кандидатами
В середине1950х годов,когда политологи впервые попыталис ь объяснить поведение кандидатов на выборах при помощи теоретико-игровых моделей,получ енный выше результат(согласно которому в ходе избирательной кампании оба кандидата принимают одну и ту же политическую программу)достаточно хорошо соответствовал реальной пол итической обстановке.В США(а именно там была сосредоточена деятельность значительной части исследователей)программы представителей двух основных политических партий — республиканцев и демократов — не слишком сильно отличались друг от друга по основным вопросам,касающимся национальной экономики.В частности,большинство республиканцев приня ло так называемый «Новый курс» президента от демократической партии Франка Рузвельта,пр едполагавший значительное перераспределение доходов от более состоятельных граждан к бедным.Однако на протяжении последующих десятилетий позиция республиканцев поменялась;она стала в значительной мере отражать интересы наиболее обеспеченной части населения. Наблюдавшееся расхождение политических программ партий(и кандидатов,которые представл яли их на выборах)бросило вызов ученым:как можно,при помощи формальной логики,объяснить наблюдавшиеся тенденции? Очевидно,что предпосылок,заложенных в самую простую моде ль политической конкуренции, описанную выше,было недостаточно.
Возможное объяснение состоит в том,что сами кандидаты могу т быть заинтересованы в реализации каких-то конкретных политических программ.Та кая модель была рассмотрена в работах Уиттмена(1979)и Кальверта(1985).Обозначим за ai [0, 1] наилучшую альтернативу кандидата i = 1, 2 (которая является параметром модели).Пусть,как и раньше, стратегия каждого кандидата i — его политическая программа si [0, 1] (которая может отличаться
от ai).Обозначим за Pi вероятность того,что кандидат |
i выиграет выборы.Пусть выигрыш |
|||||
кандидатов составляет |
|
|
|
|
|
|
U1 |
= |
λP1 − (P1|a1 − s1| + P2 |
|a1 |
− s2 |
|) |
(1.52) |
U2 |
= |
λP2 − (P1|a2 − s1| + P2 |
|a2 |
− s2 |
|) . |
(1.53) |
Здесь мы предполагаем,что кандидату небезразлична как сам а победа на выборах,так и политическая программа победившего кандидата(кем бы он ни был) .Второе слагаемое в функции полезности — ожидаемый ущерб кандидата i от реализации победителем программы,возможно отличающейся от его собственной наилучшей альтернативы ai.Параметр λ [0, 1] отражает относительную важность победы на выборах по сравнению с реализацией наилучшей политической программы.
Осталось определить вероятности победы кандидатов P1, P2.Пусть кандидат побеждает на выборах только в том случае,когда он набирает больше полови ны голосов.Пусть s1 < s2. Избиратель с наилучшей альтернативой v¯ = s1+2 s2 будет безразличен между программами двух кандидатов.Все избиратели с позициями v < v¯ проголосуют за кандидата1,с позициями v > v¯
— за кандидата2.Предположим,что каждый кандидат побеждае т только если он получает голоса более половины избирателей.Следовательно,при vm < v¯ побеждает кандидат1,при vm > v¯ побеждает кандидат2,при vm = v¯ каждый побеждает с вероятностью 12 .
Предположим,что кандидаты знают об избирателях следующее :наилучшая альтернатива медианного избирателя — случайная величина,равномерно ра спределенная на отрезке [12 − 21b , 12 + 21b ].Величина b ≥ 1 отражает степень информированности кандидатов о своем электорате. Чем она выше,тем сильнее изменения политических программ в лияют на вероятности победы

40 ГЛАВА1.СТАТИЧЕСКИЕ ИГРЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ
P1, P2.Это предположение дает нам следующие вероятности побед ка ндидатов при s1 < s2:
|
|
0, s1+2 s2 ≤ 21 − |
1 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
2b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
P1 = |
|
|
|
|
− |
|
|
+ |
2 , |
|
|
|
|
|
|
(2 |
− |
|
|
|
|
, 2 + |
|
|
|
) |
P2 = 1 |
− |
P1. |
(1.54) |
||||||||
2 |
|
|
|
1b |
2 |
|
2b |
2b |
||||||||||||||||||||||||||||||
|
|
1, s1+2 s2 |
1) |
|
21 |
+ |
, |
|
1 |
1 1 |
1 |
|
|
|
|
|||||||||||||||||||||||
|
|
b(s1+s2 |
|
|
|
|
1 |
|
s1+s2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
≥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Найдем равновесие в этой модели для a1 = 0, a2 = 1.Предполагая |
P1 (0, 1) и 0 < s1 < |
|||||||||||||||||||||||||||||||||||||
s2 < 1,получим условия первого порядка максимизации выигрыша ка ндидатов: |
|
|||||||||||||||||||||||||||||||||||||
|
|
∂U1 |
|
|
= −P1 + (λ − s1 + s2) |
∂P1 |
|
|
|
(1.55) |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
= 0 |
|
|
|||||||||||||||||||||||||
|
|
|
∂s1 |
|
|
∂s1 |
|
|
||||||||||||||||||||||||||||||
|
|
∂U2 |
|
|
= 1 − P1 − (λ − s1 + s2) |
∂P1 |
= 0. |
|
|
(1.56) |
||||||||||||||||||||||||||||
|
|
|
∂s2 |
|
|
|
∂s2 |
|
|
|||||||||||||||||||||||||||||
При λ = 0 получим |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
s1 = |
|
|
− |
|
, |
s2 |
= |
|
|
+ |
|
|
. |
|
|
|
(1.57) |
|||||||||||||
|
|
|
|
|
|
|
|
2 |
2b |
2 |
2b |
|
|
|
||||||||||||||||||||||||
Выходит так:чем выше |
b,тем ближе позиции кандидатов к ожидаемой позиции медианно - |
|||||||||||||||||||||||||||||||||||||
го избирателя 21 .Действительно,предположим,что кандидата |
i интересует только реализация |
|||||||||||||||||||||||||||||||||||||
программы,наиболее близкой к своей наилучшей альтернатив е ai.Кандидат стоит перед дилеммой.С одной стороны,чем ближе его позиция yi к ожидаемой позиции медианного избирателя, тем выше вероятность,что он выиграет выборы.С другой сторо ны,это снижает его полезность в случае победы.Чем выше неопределенность относительно по зиции медианного избирателя, тем ближе будет политическая программа кандидата к его наилучшей альтернативе.Отметим, что при b = ∞ равновесные политические программы совпадают с наилучшей альтернативой медианного избирателя,несмотря на то,что в их функции поле зности напрямую не входит победа на выборах.
ПриложениеA.Доказательство теоремы Нэша.
Доказательство теоремы Нэша является неконструктивным.М ы показываем,что для некоторого точечно-множественного отображения(определяемого через наилучшую реакцию игроков на действия остальных)существует неподвижная точка.Та же идея используется и при доказательстве многих других результатов в теории игр.
Сформулируем сначала вспомогательный результат.Если S — некоторое множество,то за 2S обозначим множество всех подмножеств S.
Теорема4 (Какутани, 1941).Пусть S — непустое,компактное и выпуклое подмножество Евклидового пространства.Пусть r : S → 2S — точечно-множественное отображение,такое,что
1.r(s) является непустым и выпуклым для всех s S.
2.r(·) имеет замкнутый график.То есть если (sn, sˆn) → (s, sˆ) — последовательность,такая, что sˆn r(sn) для всех n, то sˆ r(s).
тогда r(·) имеет неподвижную точку.
На рисунке1.12представлены два примера точечно-множеств енных отображений.В обоих случаях, S = [0, 1].На рисунке1.12(a), r(·) удовлетворяет всем условиям теоремы Какутани. Для s ̸= 12 множества r(s) состоят из единственного элемента,в то время как r(12 ) = [14 , 34 ]. Это отображение имеет неподвижную точку s = 12 , так как 12 r(12 ).Это видно из графика,так как именно в этой точке график r(·) пересекается с графиком функции f(s) = s.
