game_theory

Легко убедиться,что это действиетельно равновесие.Дейст вие a является оптимальным по

uS(t, m, a(m)),что соответствует определению равновесия.

Такое равновесие является неинформативным,так как вера иг рока R не зависит от сообщений m.Все возможные отклонения от сигнала m¯ воспринимаются как «пустой треп»:увидев сигнал m ̸= m¯ ,игрок R считает,что у каждого типа игрока S была одинаковая вероятность совершить такое отклонение.Таким образом,сообщения игро ка S не оказывают влияния на веру игрока R,которая равна априорному распределению типов игроков p(·).

Пример. Вот игра с сообщениями,в которой существует разделяющее ра вновесие:

ИгрокS t1 t2

Заметим,что это — не матричная запись статической игры,изв естная нам по Главе1. Игроки ходят по очереди;каждый столбец соответствует одно му из двух типов Игрока1, каждая строка — одному из двух возможных действий Игрока2.М ножество возможных сигналов для Игрока1совпадает с множеством его типов,но вы игрыш игроков зависит только от типа Игрока1,но не от его сигнала.Пусть p(t1) (0, 1).Очевидно,что равновесием является m(t1) = t1, m(t2) = 2, a(m1) = a1, a(m2) = a2.

Пример. Рассмотрим теперь игру с сообщениями,в которой у игрока S три возможных типа,которые равновероятны,а у игрока R — три варианта действий.Пусть выигрыши игроков таковы:

В такой игре в равновесии информация не может раскрываться полностью.Действительно,

пусть игрок S правдиво сообщает свои типы: m(t1) = t1, m(t2) = t2, m(t3) = t3.Тогда игрок R будет реагировать на эти сообщения следующим образом: a(t1) = a1, a(t2) = a2, a(t3) = a3.

Однако uS(t1, a(t1)) < uS(t1, a(t2)),то если игрок R верит в то,что игрок S правдиво сообщает свой тип,и игрок S имеет тип t1,то игроку S выгодно соврать,назвавшись типом t2.

Тем не менее существует равновесие,в котором m(t3) = t3.Сообщение m(t3) = t3 будет достоверным:если a(t3) = a3,то игроку S не будет выгодно сообщать m(t1) = t3 или m(t2) = t3. Можно продолжить построение этого равновесия.Предположи м,что игрок R,получив сигнал t1,с равной вероятностью считает,что игрок S имеет тип t1 или t2.При такой системе вер, оптимальными действиями игрока R будет a(t1) = a(t2) = a2.При сигналах m(t1) = m(t2)t1 или m(t1) = m(t2) = t2 такая система вер будет оправдана с точки зрения правила Байеса. Например,при m(t1) = m(t2)t1,

Мы получаем равновесие,в котором происходит частичное рас крытие информации:игрок R не может отличить игрока S типа t1 от игрока типа t2,но если игрок S имеет тип t3,то это становится известно.

????????????????????????????????

182 ГЛАВА4.ДИНАМИЧЕСКИЕ ИГРЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ

4.3Примеры

4.3.1Раскрытие информации в играх с сообщениями

В двух примерах на страницах180–181мы рассмотрели простые примеры игр с сообщениями. В первой такой игре возможно равновесие с полным раскрытием информации,когда игрок R всегда узнает тип игрока S.Во второй игре этого не происходит — игрок R не может отличить t1 от t2.Почему в одних играш происходит раскрытие информации,а в д ругих — нет?Общая закономерность здесь такова:чем сильнее совпадают интере сы двух игроков,тем больше информации раскрывается.В первом примере мы видели полное совпадение интересов,во втором — частичное(если S имеет тип t3,то полезности обоих игроков максимизируются при a = a3,если t1 или t2 — то не все так просто).В случае,когда интересы не совпадают

— как,например,в следующем примере — будет существовать то лько смешивающее равновесие:

Рассмотрим более общую модель,предложенную Кроуфордом и С обелем(1982).Пусть t — некая случайная величина,равномерно распределенная на от резка [0, 1].Значение этой величины известно игроку S,но не игроку R.Пусть a [0, 1] — действие,предпринимаемое игроком R.Выигрыши игроков зависят от t и a следующим образом:

Таким образом,фукнция полезности выигрыш каждого игрока я вляется однопиковой по a, при - чем наилучшая альтернатива — величина,известная только иг року S;предпочтения игроков отличаются на величину b.

Можно привести много жизненных примеров такой игры.Наприм ер,игрок S является экспертом в одной из областей экономической политики,скажем, председателем соотвествующего парламентского комитета.Он потратил много времени на изуч ение своей предметной области,и поэтому именно ему известна величина t — оптимальная на данный момент времени политика.Игрок R в таком случае будет представитель большинства в парламенте,который и определяет величину a — политику,которая будет реализована.Проблема состоит в т ом,что интересы парламентского большинства могут отличаться от интересов председателя комитета. Пусть,например,речь идет о необходимой величине сокращен ия или увеличения расходов на образование.Председатель комитета может сам быть из профе ссорской среды,что делает его склонным рекомендовать более высокие затраты на образование,чем порекомендовал бы человек с другим прошлым.Это не может не быть известно парламент скому большинству,которое обязано учитывать разницу во взглядах — выражаемую в нашей модели величиной b — при принятии решения.Получется так,что при b > 0 у нас не может быть полного раскрытия информации.Если мы предположим,что большинство верит предс едателю комитета и проводит ту политику,которую он рекомендует — a = t — то председатель комитета будет врать,максимизируя свою полезность при m = t + b.Но если он ведет себя таким образом,то большинство будет учитывать эту разницу во взглядах,выбирая действие a = t − b.

Предположим,что стратегия игрока S имеет следующий вид.Пусть X1, X2, . . . , Xn — под -

Каким будет реакция игрока R на такую сигнальную стратегию?Вера игрока R определяется по правилу Байеса для всех m [0, 1]:если m Xi,то тип игрока S будет случайной величиной,равномерно распределенной на Xi.Тогда задача игрока R —

при t Xi.

Теперь убедимся,что в любом совершенном байесовом равнове сии мы обязаны иметь Xi =

t1 X1, t2 X2 мы имеем t1 > t2,то мы получаем противоречие:либо |x1−(t1+b)| > |x2−(t1+b)|, либо |x2 − (t2 + b)| > |x1 − (t2 + b)|.Этого не может быть в равновесии,ибо мы получим

uS(t1, a(m(t1))) < uS(t1, a(m(t2))), либо uS(t2, a(m(t2))) < uS(t2, a(m(t1))).

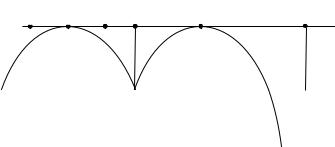
Получается,что каждый отрезок Xi+1 на 4b единиц длиннее предыдущего(рисунок4.13).Для того,чтобы найти равновесие,нам необходимо найти x1, . . . , xn+1,такие,что xn = 1, и выпол - няется(4.46)для всех i = 1, . . . , n − 1.

xi−1 x¯i−1 xi xi + b x¯i xi+1

Рис. 4.13:Соотношение xi и xi+1 в игре с сообщениями.

Если x0 = 0, то мы получим (x2 − x1) = x1 + 4b, (x3 − x2) = x1 + 8b,и так далее,вплоть до (1 − xn−1) = x1 + 4(n − 1)b.Суммируя,получается

i=1

184 ГЛАВА4.ДИНАМИЧЕСКИЕ ИГРЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ

Равновесиеcчастичным раскрытием информации существует, если есть x1 (0, 1) и целое число n ≥ 2,которые удовлетворяют уравнению(4.47)для данного b > 0.

Мы можем посмотреть,как степень раскрытия информации в рав новесии зависит от параметра b,опретеляющего соответствие интересов двух игроков.Чем в ыше n,тем больше вероятность того,что информации раскрывается.Можно дать формал ьное определение «раскрытию информации»,как матожиданию разности между проводимой по литикой a и сигналом t, полу - чаемым игроком S.Формально,мы определим

Для равновесия,в котором n = 1,то есть раскрытия информации не происходит,мы имеем a(m(t)) = 12 для всех t,и,соответственно, Ir(1) = 14 . Для n = 2,уравнение(4.47)дает нам x1 = 1−24b .Равновесие существует только при b < 14 ,то есть даже для минимального уровня раскрытия информации необходимо,чтобы интересы двух игро ков были достаточно схожи.В

таком случае,мы получим Ir(2) = 14 (x21 + (1 − x1)2) = 18 + 2b2 < 14 .Очевидно,что чем n — то есть число категорий сигналов t,между которыми может различать игрок R — тем меньше Ir.

Однако равновесие высоким n возможно только при достаточно малом b.Действительно,из

При b → 0,мы получаем возможность все большего раскрытия информаци и.Будет ли исход игры оптимальным по Парето при достаточно большом b?Для оптимальности по Парето необходимо,чтобы для всех t,не существовало такой a′ [0, 1], что uR(t, a′) ≥ uR(t, a(m(t))) и uS(t, a′) ≥ uS(t, a(m(t))),хотя бы с одним строго выполняющемся неравенством.Это озн ачает, что для всех t,мы должны иметь a(m(t)) [t, t + b].Но это условие не выполняется при всех положительных b:например,мы всегда получим x¯i−1 = a(xi) < xi < xi + b.Мы в очередной раз убеждаемся,что асимметрия информации вредит обоим игрока м.

4.3.2Экономическая теория политического популизма

Неравенство доходов свойственно большинству развивающихся стран.Неудивительно,что часто политическая программа президентского кандидата призывает к перераспределению доходов в пользу малоимущих слоев населения.Однако,раз за разо м,демократически выбранные политики-«популисты» принимают слишком жествие меры,кот орые в краткосрочной перспективе действительно дают снижение неравенства,но в среднес рочной — приводят к макроэкономическому кризису.Как правило,такая «популистская» поли тика состоит в чрезмерном росте государственных расходов.Этот рост финансируется за счет двух источников.Во-первых,это рост налогообложения,создающий отрицательные стимулы дл я развития бизнеса.Во-вторых, это увеличение государственного долга,которгое может при вести к долговому кризису — дефолту на рынке государственных облигаций,снижению стоимо сти национальной валюты,и болезненному снижению государственных расходов,либо вкл ючению «печатного станка» и высокой инфляции.В итоге положение широких слоев населения — во имя которых и проводились радикальные реформы — на самом деле ухудшается,хотя не наст олько,насколько ухудшается положение элиты и среднего класса.

Если рассматривать политическую программу кандидата как точку на шкале «лево-право», где левая политика предполагает распределение от богатых к малоимущим,то по сути получается,что некоторые кандидаты занимают ультра-левую поз ицию,более левую,чем предпочтения большинства населения.При этом основой риторики та ких политиков — как во время

избирательной кампании,так и после нее — является проводим ая ими борьба за интересы простого народа против небольшой и привилегированногй элиты. Пожалуй,наиболее известным политиком такого плана является Уго Чавес в Венесуэле — однако список можно продолжить: Боливия(Эво Моралес),Перу(Алан Гарсиа),Эквадор(Рафаэт Коррера),и так далее.

Конечно же,такие вещи всегда имеют простое объяснение:нар од(а,подчас,и сам политик) не имеют представления о том,во какие последствия будут име ть предлагаемые реформы в ближайшем будущем.Возможно,что отчасти это так и есть.Одн ако такой ход рассуждения не приветствуется в академической среде:ведь при помощи выбо рочных предположений о нерациональности тех или иных игроков можно объяснить практически все происходящее в нашем мире.Б´ольшим и более интересным вызовом всегда является нахождение формального объяснения.Как должна быть устроена система стимулов и информ ационная структура,чтобы такое могло произойти с рациональными,все понимающими изб ирателями и политиками?

Асемоглу,Егоров и Сонин(2011)объясняют этот феномен,не п рибегая к предположению о нерациональности политиков или избирателей.Дело в том,ч то в странах Латинской Америки — как и во многих других странах — политики часто маскируют свои истинные интересы. Бывает так,что кандидат в президенты обещает проводить спр аведливую по отношению к большинству граждан политику,а в итоге оказывается агенто м влияния небольшой и очень богатой элиты,и проводит политику,направленную на обогащен ие немногих за счет большинства (как правило,это достигается за счет низких налогов,попус тительства коррупции,и поддержке монополий).Как политику убедить своих граждан,что он — н е волк в овечьей шкуре,что его собственные предпочтения действительно совпадают с интересами граждан?Возможный способ так сделать — после избрания начать проводить политику,совершенно неприемлемую для потенциального представителя интересов элиты.Настол ько неприемлемую,что публика станет рассуждать так:«Наш президент,господинX,действи тельно хочет того же,чего хотим мы.Если бы он представлял интересы ненавистных нам богачей ,то не стал бы себя так вести

— даже если это позволило бы ему нас обмануть и заставить нас избрать его на новый срок». Рассмотрим формальную модель,проводящую эту аргументаци ю.Пусть существуют четыре игрока — находящийся у власти президент,его возможный пр еемник,и две группы граждан: большинство и элита.В момент времени t = 1 президент выбирает,какую экономическую программу y1 R ему следует проводить.В момент времени t = 2 происходят выборы:большинство решает,оставить президента у власти,или избрать нового.В момент времени t = 3 переизбранный президент(или новоизбранный преемник)проводят полит ику y2 R.Затем реализуются

выигрыши.

Полезность гражданина зависит от проводимой политики в обоих периодах,и от того,к

где vm, ve — наилучшие альтернативы каждого из двух типов граждан.Так им образом,граждане обладают однопиковыми предпочтениями относительно политики.Будем считать,что большинство предпочитает более левую политику(то есть бол ьше перераспределения),чем

элита: vm = 0 < ve.

Выигрыш президента равен

переизбран.Величина ap отражает наилучшую альтернативу президента.Таким образо м,мы

политик мог убедить избирателей в том,что при наступлении в торого президентского срока он внезапно не предаст их интересы,оказавшить на самом деле проводником интересов элит, «волком в овечьей шкуре» с ap = ve.Каков смысл условия b > (1 − p)ve2?Во-первых,цен- ность президентского кресла b должна быть достаточно большой — иначе президент от элиты, имеющий ap = ve,не будет готов имитировать радикально левую политику для т ого,чтобы обмануть избирателей и переизбраться.Во-вторых,вероятнос ть p того,что предпочтения президента совпадают с предпочтениями большинства избирателей,должна быть низка.И,наконец, в-третьих,предпочтения элиты не должны слишком сильно отл ичаться от предпочтений большинства.Полезность избирателей и политиков убывает пропо рционально квадрату расстояния между их наилучшей альтернативой и реализуемой политикой. Если разница между позициями элиты и большинства будет слишком большой,то издержки,свя занные с имитацией поведения «народного» политика,будут слишком высоки.

Найдем второе условие для разделяющего равновесия.Полити ка y1m не должна быть слишком левой,иначе «народный» президент с ap = vm = 0 просто предпочтет выбрать y1 = 0, упуская возможность избраться на второй срок.Данное услов ие будет таким:

Из условий(4.60)и(4.63)следует,что при b ≤ (1 − p)ve2 разделяющее равновесие с системой вер(4.57)всегда существует,а при b > (1 − p)ve2,необходимым и достаточным условием существования разделяющего равновесия является

Это условие всегда выполняется;следовательно,разделяющ ее равновесие существует всегда, причем при b > (1 − p)ve2 в любом таком равновесии с системой вер(4.57)мы будем иметь y1m < 0,то есть политик,чьи интересы совпадают с интересами больи нства избирателей,будет реализовывать политику более радикальную,чем та,кото рую предпочитает большинство избирателей и он сам.4

4.3.3Репутация и кредитно-денежная политика центральног о банка

Вернемся к задаче установки кредитно-денежной политики центральным банком,рассмотренную на стр. 88–91.Напомним,что в этой задаче рассмотрена дв ухпериодная игра,в которой сначала публика выбирает уровень инфляционных ожиданий,з атем центральный банк реализует кредитно-денежную политику,определяющую уровень инфляции.Показано,что при определенных предположениях относительно целевых функций публики и центрального банка,в совершенном по подыграм равновесии уровень инфляции б удет неоптимально высок.В

4Приведенная здесь модель является адаптацией работы Асемоглу,Егорова и Сонина(2011).В исходной работе модель строилась несколько по-другому.Предполага лось,что избиратели не наблюдают политику y1, реализуемую президентом в момент времени t = 1. Вместо этого им становится известна величина z = y1 +e, где e — не наблюдаемая избирателями случайная величина , распределенная с нулевым матожиданием и ненулевой плотностью f(·) на (−∞, ∞). Таким образом , еслиy1m и y1e — политика , реализуемая президентом каждого

Это дает нам единственное равновесие,но несколько усложня ет доказательство его существования и анализ сравнительной статики.В исходной формулировке,качестве нная зависимость политики «народного» кандидата от параметров модели та же,что и для условия(4.60).

188 ГЛАВА4.ДИНАМИЧЕСКИЕ ИГРЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ

рассмотренной задаче Парето-оптимальным уровнем инфляции является нулевая инфляция; однако если публика ожидает нулевую инфляцию,то у централь ного банка будет стимул обмануть эти ожидания для того,чтобы добиться увеличения ВВП.П ублика,зная,что центральный банк будет вести себя подобным образом,предвидит такой(по ложительный)уровень инфляции, что выигрыш центрального банка от установки уровня инфляции выше ожидаемого полностью компенсируется его проигрышем от высокой инфляции.

Существуют ли силы,могущие заставить центральный банк достоверно обещать публике низкую инфляцию?Один из таких механизмов — репутационный. Если центральный банк обладает репутацией принципиального борца с высокой инфляцией,то публика может верить его обещаниям не поднимать цены.Обманув ожидания публики одна жды,центральный банк сможет добиться временного повышения ВВП,но при этом потеряет репутацию:в будущем публика будет знать,что центральный банк будет пытаться стимулиро вать ВВП при помощи кредитноденежной политики,и будет ожидать высокую инфляцию.Таким образом,репутация принципиального сторонника низкой инфляции может быть выгодна для руководителя центрального банка, даже если эта репутация не соответствует действительности.Это расс уждение впервые было предложено Бэрро(1986)и Бакусои и Дриффилом(1985).Т еоретико-игровая модель, рассмотреная здесь и формализующая это рассуждение,взята из учебника Ромера(2006,стр.

511–514).

Пусть взаимодействие центрального банка и публики происходит на протяжении двух периодов.В каждый момент времени t = 1, 2,публика формирует инфляционный ожидания πte;

В игре существует три игрока:публика в момент времени t = 1,публика в момент времени

Центральный банк может быть двух типов.Первый тип — оппорту нист,имеющий функцию

где π = 0 — оптимальный уровень инфляции , β < 1 — фактор дисконта.Второй тип центрального центрального банка — принципиальный борец с инфляцией,который устанавливает π1 = π2 = 0 вне зависимости от того,каковы инфляционные ожидания публ ики.Пусть p — вероятность того,что центральный банк окажется оппортуни стом.

Если центральный банк является принципиальным борцом с инфляцией,то его поведение не определяется внутри модели.Нас интересует,как поведет се бя банк-оппортунист.Рассмотрим,

тип1после момента времени t = 1.Математическое ожидание выигрыша публики в момент

5Эта функция полезности немного отличается от функции(2.65 ),рассмотренной в примере на стр. 88–91.В данном случае функция полезности центрального банка является линейной по ВВП(а не квадратичной,как в прошлом примере).Это упрощение не критично для основного р езультата,который основан на предположении, что целевая функция центрального банка нелинейно зависит от уровня инфляции .

Найдем λ.Очевидно,что если π1 ̸= 0, то λ = 0 (поскольку принципиальный банкир всегда выбирает нулевую инфляцию).Очевидно,что для банкива второг о типа любая стратегия,пред-

где qp — вероятность того,что банк будет иметь первый тип и выберет нулевую инфляцию, 1−p — вероятность того,что банк будет иметь второй тип(что авто матически означает π1 = 0).

Найдем выигрыш центрального банка,если в момент времени t = 1 он выбирает π1 = 0. Мы получим

3.Равновесие,в котором q (0, 1),то есть центральный банк играет смешанную стратегию.

кие инфляционные ожидания на завтрашний день),и устойчива к альтернативным спецификацифям модели.Одним из выводов сравнительной статики сос тоит в том,что на инфляцию влияет фактор дисконта центрального банка:низкоинфляцио нное равновесие возможно только при при достаточно высоком β,то есть если банк ценит будущий период достаточно высоко по сравнению с сегодняшним.

Эмпирические исследования подтверждают предположение о том,что предпочтения центрального банка могут влиять на уровень инфляции.Алесина и Саммерс(1993)показали,что инфляция значимо зависит от степени независимости центрального банка.В тех странах,где председатель центрального банка назначается редко и на долгий срок,а также не вынужден отчитываться перед парламентом или исполнительной властью,инфляция ниже.Действительно,если центральный банк подвержен влиянию политической к онъюнктуры(которая может

4.3.4Подотчетность политиков и выборы.

Бизли и Смарт(2007),Бэрро(1971),Фереджон(1986)

Рассмотрим некоторую страну,в которой политик(президент )должен,в течение двух электоральных циклов,принять решение относительно того,как р аспределять налоги,собранные с населения,между производством общественных благ и нецел евым использованием(то бишь воровством).Пусть игра имеет следующую структуру.

Этап1 Природа определяет типы действующего президента t1 {b, g} и его конкурента на выборах t′1 {b, g}.Каждый политик может быть одного из двух типов:честный( g),или коррупционер( b).Типы политиков независимы,причем P (t1 = g) = P (t2 = g) = π.

Этап2 Действующий президент решает,какова должна быть ставка на логообложения τ1 [0, 1],и как следует собранные налоги перераспределить между про изводством общественных благ и нецелевыми расходами s1.Пусть

где G1 — объем производства общественного блага во время первого электорального цикла, θ — издержки производства1единицы общественного блага, s1 — объем коррупции в первом электоральном цикле.Величина θ может принимать значения θ {H, L},причем P (θ = H) = q.Значение этой величины известно только действующему през иденту.

Этап3 Проходят выборы.Публика выбирает,кто должен стать следую щим президентом:действующий президент,или претендент.

Этап4 Наступает следующий электоральный цикл.Новоизбранный пр езидент решает,какой должна быть ставка налогообложения τ2 [0, 1],и как следует собранные налоги перераспределить между производством общественных благ и нецелевыми расходами s2. Как и раньше,действует ограничение