game_theory

Таким образом,наилучший отклик игрока1на линейную страте гию игрока2— также играть линейную стратегию.Мы не просто нашли равновесие в классе л инейных стратегий.Мы нашли пару линейных стратегий,которая является равновесием — уч итывая,что каждый из игрок может выбрать любую другую стратегию.

Из(3.51)получим,что β2 = 23 и α2 = α31 . Из (3.51) получим α1 = 13 (α31 + 23 ), или α1 = 14 , β1 = 23 , и α2 = 121 .Является ли полученное равновесие эффективным?Нет.Торг овля происходит

только в том случае,когда p1 ≤ p2, или 23 c + 14 ≤ 23 v + 121 , или c ≤ v − 14 ,в то время как Паретооптимальность предполагает обмен в том случае,если c ≤ v.

Предвыборная конкуренция с идеологическими кандидатами

В некоторой стране проходят выборы.В них участвуют два канд идата.Предположим,что каждый кандидат может предложить избирателям одну из трех программ:левую,правую, или центристскую.Соответственно,множество действий для каждого кандидата i = 1, 2 будет Ai = {L, C, R}, где L — левая программа, C — центральная, R — правая.Кандидаты не знают предпочтений избирателей.Им известно,что с вероятностью α медианный избиратель будет центристом,с вероятностью 1−2α — левым или правым.Следовательно,вероятность того,что первый кандидат выиграет выборы,зависит от программ канди датов следующим образом:

с равной вероятностью голосует за каждого из кандидатов.Та кже,если один кандидат левый, а другой-правый,то избиратель-центрист голосует в равной вероятностью за обоих.

Будем считать,что выигрыш каждого кандидата зависит тольк о от того,какова программа победившего кандидата.Кандидат1может быть двух типов:це нтрист или левый: T1 = {L, C}. Кандидат2может быть центристом или правым: T2 = {C, R}.Пусть β — вероятность того, что каждый из кандидатов является центристом.Будем считат ь,что типы кандидатов независимы.Выигрыш каждого кандидата составляет 0 если реализовывается программа,равная его типу, −1,если реализуется программа,отличающаяся от его типа на од ин шаг(например, если кандидат — центрист,а побеждает кандидат с левой прогр аммой),и −c,если реализуется программа,отличающаяся от его типа на два шага(если кандид ат — левый,а победил правый, или наоборот),где c ≥ 2.

Кандидат1не станет выбирать a1 = R,так как это действие доминируется(причем строго) действием a1 = C при обоих типах кандидата1.Аналогично,второй кандидат не будет играть L.Стратегией кандидата1в этой модели будут пара (pL, pC) — вероятности,что кандидат1 выберет действие a1 = L в случае,если его тип L или C.Аналогично,стратегией кандидата2 будет пара (qR, qC) — вероятности выбрать действие a2 = R в зависимости от собственного типа.

124 ГЛАВА3.СТАТИЧЕСКИЕ ИГРЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ

Рассмотрим упрощенный пример из работы Полфри,Гоури и Холь та(2001).Есть такая игра 2 × 2:

Это — игра производства общественного блага при технологии «слабое звено».Два игрока решают,сколько усилий —1единицу( L)или2единицы( H)потратить на производство общественного блага.Количество произведенного блага равняет ся минимуму затраченных усилий. Издержки одной единицы усилий равны c ≤ 1.

При c ≤ 1 в этой игре два равновесия в чистых стратегиях: (H, H) и (L, L) и одно равновесие в смешанных стратегиях,в котором каждый игрок выбирает H с вероятностью c.То есть в смешанном равновесии,высокий уровень производства общес твенного блага тем вероятней,чем выше издержки его производства.Этот результат противоинт уитивен.Эксперименты с такими играми(например,Гоури и Хольт, 2005)показывают,что част ота,с которой игроки выбирают низкие уровни усилий,возрастает с уровнем издержек c.

Рассмотрим теперь модифицированную игру,в которой к выигр ышу каждого игрока i = 1, 2

Рис. 3.5:Равновесие дискретного отклика в игре с производс твом общественных благ.

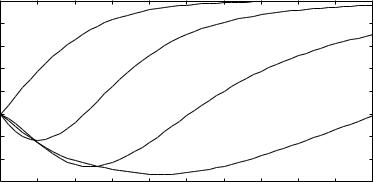
На рисунке3.5показана зависимость равновесного p от c при разных значениях λ.Действительно,при более высоком значении c,каждый игрок с большей вероятностью выберет L. То есть переход к модели,в которой у полезностей игроков есть с лучайная(и ненаблюдаемая)компонента ϵ,позволяет нам получить сравнительную статику,которая со ответствует как нашей интуиции,так и экспериментальным данным.

Рис. 3.7:Равновесие в игре «сорокорожка» со стохастически ми функциями полезности.

большинства значений λ верно соотношение p1 < q1 < p2 < q2,то есть вероятность того,что игрок выберет действие T и заберет приз тем выше,чем ближе к концу игры мы подходим.Эт о соответствует тому,что мы наблюдаем в большинстве экономи ческих экспериментов с игрой «сороконожка».Во-вторых,при увеличении λ — то есть при снижении дисперсии функции полезности — поведенческие стратегии игроков стремятся к равновесию в игре с совершенной информацией,в которой игроки всегда забирают приз во всех в ершинах игры.Наконец,в- третьих, (и это наиболее интересно)при малых значениях λ вероятности p1, p2, q1 и q2 убывают с λ.

3.2Дизайн механизмов

Находя равновесие в теоретико-игровой модели,мы даем отве т на вопрос:Как поведут себя игроки,будучи поставленными в определенные условия?Дизайн механизмов — это раздел теории игр,который изучает обратную задачу:Какие правила игры не обходимо создать для того,чтобы в равновесии игроки реализовывали данный профиль действий?Задача дизайна механизмов имеет большое практические значение.Проведение аукционо в — первый пример,приходящий в голову.Мировой объем торгов на аукционах(как по продажам товаров частным лицам,так и по государственным закупкам)исчисляется сотнями миллиар дов долларов в год.Как правильно прописать правила аукциона,чтобы товар был продан по наи большей цене,а возможность сговора между покупателями была минимальна?Другая област ь,в которой дизайн механизмов играет важную роль — раздел имущества во время бракоразводных процессов.Бывшие супруги должны договориться,как поделить совместное имущество ,которое состоит из большего количества разных предметов.Каждый по-разному ценит разн ые предметы,и хотелось бы(с точки зрения максимизации суммарного благосостояния),чт обы каждая вещь досталась тому, кто ее больше ценит.Задачей представляется так построить п роцесс раздела имущества,что каждый супруг на вопрос «во сколько вы оцениваете этот предмет» отвечал бы правдиво.

3.2.2Нэш-реализуемость механизмов

Посмотрим,в каких случаях мы можем ожидать,что значения да нной функции общественного выбора будут являться равновесием Нэша в игре с неполной информацией.

Определение33 Механизм M Нэш-реализует правило общественного выбора f,если для всех t T ,мы имеем g(s (t)) = f(t), где s — равновесие Нэша в игре G(M).

Рассмотрим,в качестве примера,задачу продажи товара на ау кционе с двумя покупателями.Пусть действует правило аукциона второй цены:покупате ли одновременно делают заявки, товар продается покупателю с наибольшей заявкой,причем пл атит он сумму,равную наименьшей заявке.В первой главе на странице9мы доказали,что в рав новесии в этом аукционе заявка каждого покупателя равна его оценке стоимости товара.То есть,если t1, t2 — типы покупателей,соответствующие их оценкам стоимости товара ,то механизм «аукцион второй цены» Нэш-реализует следующую функцию общественного выбора:если t1 > t2, продать товар покупателю1по цене t2,если t1 = t2 — продать товар каждому из двух покупателей с равной вероятностью,если t1 < t2 — продать покупателю2по цене t1.

Аукцион второй цены эффективен — то есть он справляется с задачей продажи товара тому покупателю,который готов заплатить больше других.Однако ,к сожалению для продавца,в аукционе второй цены покупатель практически всегда недоплачивает.Можно ли придумать правила,при которых аукцион принесет продавцу большую при быль?Возможно ли придумать такой аукцион,в котором покупатель будет отдавать продавц у все,что он готов заплатить?

На первый взгляд,задача дизайна такого механизма выглядит очень сложной.Существует множество различных вариантов организации аукциона:спус кающаяся и поднимающаяся торговля,аукционы первой и второй цены,и так далее.Можно ли их всех описать математически? К счастью,оказывается,что можно.Дадим такое определение .

Определение34 Пусть T — множество типов игроков, C — множество исходов.Механизм

M = A, g является прямым механизмом если A = T .

Если продолжить пример с продажей товара,то любой прямой ме ханизм будет предполагать,что участие покупателя в аукционе ограничивается соо бщением продавцу максимальной суммы,которую он готов заплатить за товар.Следующий резул ьтат,полученный,в том числе, Майерсоном(1979),показывает,что в задаче поиска механиз ма нам достаточно рассматривать только прямые механизмы.

когда ведущий говорит каждому игроку:«Скажи мне свой тип,и я сам сыграю за тебя твою равновесную стратегию в механизме M».Каждый игрок честно сообщит ведущему свой тип — иначе,если игрок соврет,то ведущий сыграет за него стратег ию,которая может отличаться от равновесной.

Следовательно, является равновесием Нэша в игре ¯ .

a = t G(M) Q.E.D.

Монотонность по Маскину

Что мы можем сказать про то,какие функции общественного выб ора можно Нэш-реализовать при помощи какого-то механизма?Дадим такое определение.

игроков,предписываемый ранее исход стал менее предпочтит ельным относительно какого-то другого варианта.Это свойство получило названия монотонн ости по Маскину,по имени Эрика Маскина,нобелевского лауреата.Им же(Маскин1977, 1985)б ыл доказан такой результат:

для всех i и для всех a′i Ai. Однако a не является равновесием в игре G(M) при типах игроков

Следовательно, g удовлетворяет условию монотонности. Q.E.D.

Пример.Соломонов суд.

Библейская легенда о суде мудрого царя Соломона — ранний и очень известный пример попытки решить задачу дизайна механизма:

Мудрость свою Соломон показал прежде всего на суде.Вскоре п о воцарении его пришли к нему на суд две женщины.Они жили в одном доме,и у кажд ой было по младенцу.Ночью одна из них своего младенца задавила и подло жила его к другой женщине,а живого у той взяла себе.Утром женщины стали спори ть:«живой ребенок

«Рассеките живого ребенка пополам и отдайте половину одной и половину другой». Одна из женщин при этих словах воскликнула:«отдайте лучше е й младенца,но не убивайте его!» Другая же,напротив,говорила:«рубите,пус ть не достанется ни ей ни мне».Тогда Соломон сказал:«не убивайте ребенка,а отдайте его первой женщине: она его мать».Народ услышал об этом и стал бояться царя,пото му что все увидели, какую мудрость дал ему Бог(Ветхий завет, 3-я книга Царств,г л. 3,ст. 16-—28).