20. Случайные величины. Виды случайных величин. Их сходства и отличия.

Случайная величина – переменная, которая в результате опыта в зависимости от случая принимает одно из множества значений (какое именно – неизвестно). С теоретико-множественной позиции СВ – функция, определенная на пространстве элементарных событий. Случайные величины бывают дискретные и непрерывные. Дискретная величина – принимает конечное или бесконечное счетное множество значений (можно пронумеровать натуральными числами). Непрерывная величина – это СВ, бесконечное и несчетное множество значений которой есть некоторый интервал (конечный или бесконечный) и она сплошь заполняет этот интервал. Дискретная величина задается законом распределения или функцией распределения, непрерывная СВ – функцией плотности и функцией распределения.

21. Дискретная СВ. Математическое ожидание и дисперсия. Основные законы распределения дискретных СВ (перечислить).

Д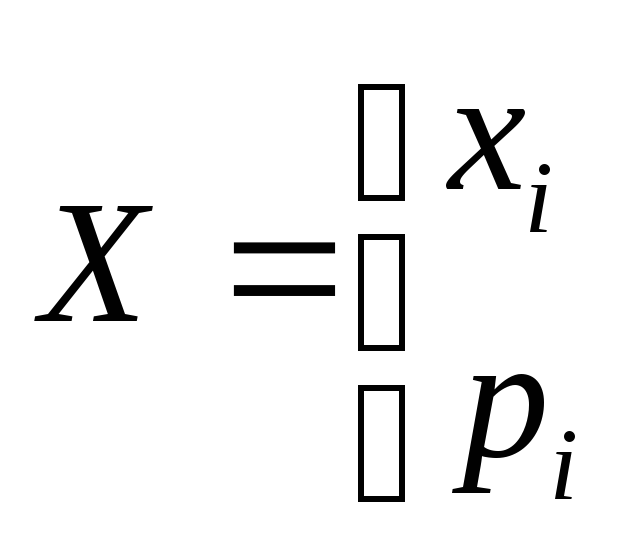искретная величина – принимает конечное или бесконечное счетное множество значений (можно пронумеровать натуральными числами). Дискретная величина задается законом распределения или функцией распределения.

Закон распределения: где х_i – значение СВ, p_i - вероятность значений.

0≤ p_i≤1 Σp_i =1

Функция распределения F(x) – функция, выражающая для каждого х вероятность того, что СВ примет значение меньше х.

Математическое ожидание – это среднее значение СВ. Для дискретной СВ , для конечных n. Если СВ принимает бесконечное, но счетное число значений, если ряд сходится, то

Дисперсия характеризует разброс, рассеяние значение СВ вокруг её мат. ожидания. Для дискретной СВ с конечным числом значений n , для СВ, принимающей бесконечное, но счетное число значений (если ряд сходится) . Основные законы распределения – биномиальный, Пуассона, отрицательный биномиальный, 1й геометрический, 2й геометрический, гипергеометрический

22. Функция распределения и ее свойства. Сходства и отличия функций распределений дискретных и непрерывных СВ.

Функция распределения F_ξ(x) – функция, выражающая для каждого х вероятность того, что ξ примет значение меньше х. F_ξ(x)=Р(ξ<x)

F(x) – интегральная функция распределения, вероятность попадания случайной точки ξ левее заданной х

Общие для дискретной и непрерывной СВ свойств функции распределения:

1) 0≤F(x)≤1, как вероятность. F(-∞)=0 F(+∞)=1 F_ξ(x)=0, ∀x≤x_min

F_ξ(x)=1 ∀x≤x_max

2) F(x) – неубывающая функция на всей числовой оси

3) Р(a≤x≤b) = F(b) – F(a)

Свойства только дискретной СВ:

4) F(x) = Функция разрывная и ступенчатая.

5) Вероятность попадания дискретной СВ в интервал (-∞; -b] равна значению функции распределения в точке, смещенной относительной b вправо на бесконечно малое значение. Р(х≤b)=F(b+0)

Cвойства функции распределения только непрерывной СВ:

4) Ф-я F(x) непрерывна в любой точке и имеет всюду непрерывную производную

23. Непрерывная случайная величина. Теорема о вероятности отдельно взятого значения. Математическое ожидание и дисперсия. Основные законы непрерывных СВ (перечислить).

Непрерывная величина – это СВ, бесконечное и несчетное множество значений которой есть некоторый интервал (конечный или бесконечный) и она сплошь заполняет этот интервал. Непрерывная СВ задается функцией плотности и функцией распределения.

Теорема о вероятности отдельно взятого значения: Вероятность любого отдельно взятого значения непрерывной величины равна 0.

Доказательство:

Математическое ожидание – это среднее значение СВ. Для непрерывной СВ

Дисперсия характеризует разброс, рассеяние значение СВ вокруг её мат. ожидания для непрерывной СВ

Основные законы распределения – Нормальный, равномерный, показательный (экспоненциальный), логнормальный, Гамма-, Пирсона, Стьюдента, Фишера - Снедекора.

24. Непрерывная случайная величина. Функции плотности вероятности и ее свойства

Непрерывная величина – это СВ, бесконечное и несчетное множество значений которой есть некоторый интервал (конечный или бесконечный) и она сплошь заполняет этот интервал. Непрерывная СВ задается функцией плотности и функцией распределения.

f(x)=F`(x) дифференциальная функция

Свойства f(x):

1. f(x)≥0 (как производная монотонно не убывающей функции.

2. Вероятность попадания в (х₁;х₂). Р(х₁≤Х≤ х₂)=

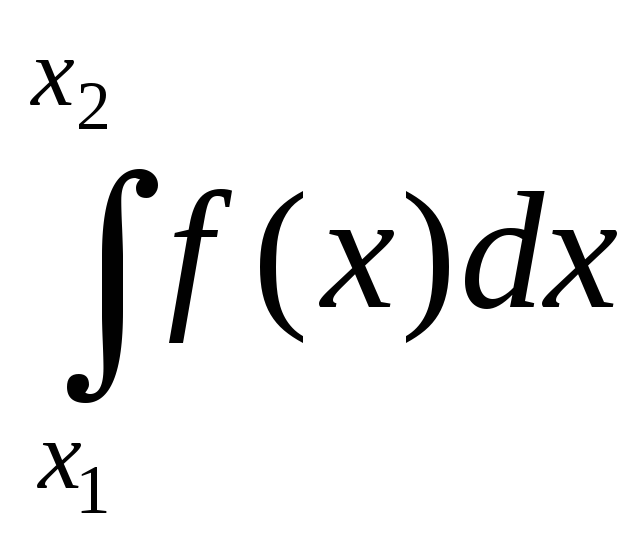
3. F(x)=

4. 

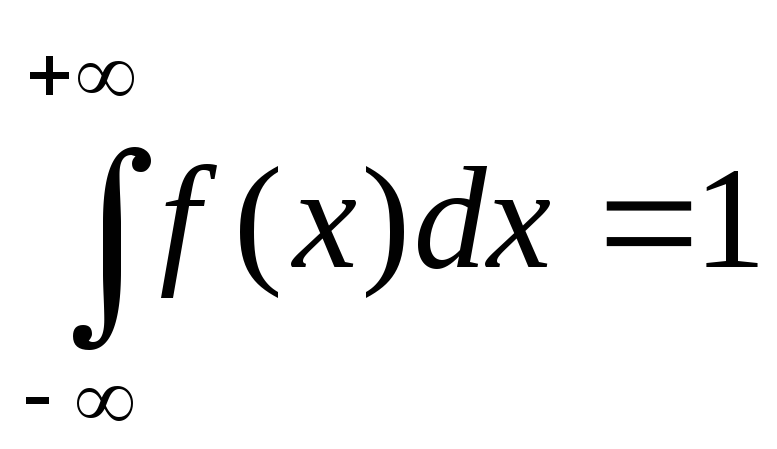
25. Математическое ожидание случайной величины. Его свойства. Отличия для независимых и зависимых СВ в расчете математического ожидания их произведения.

Математическое ожидание – это среднее значение СВ. Для дискретной СВ , для конечных n. Если СВ принимает бесконечное, но счетное число значений, если ряд сходится, то Для непрерывной СВ .

Свойства:

1. М(С)=С

2. М(СХ)=С*М(Х)

3. М(Х+У)=М(Х)+М(У)

М(Х-У)=М(Х)-М(У)

М(Х±С)=М(Х)±С

Мат. ожидание произведения независимых величин Х, У: М(ХУ)=М(Х)*М(У)

Мат. ожидание произведения двух зависимых СВ Х,У: М(ХУ)=М(Х)М(У)-cov(X,Y)

26. Понятие о центрированной и стандартной случайной величине. Их связь с исходной величиной, изменение формы и положения на координатной плоскости полигона или кривой плотности распределения вероятности.

Центрированная СВ: ẋ=х-М(х) М(ẋ)=0 D(ẋ)=D(x)

Стандартная СВ: Т= ẋ/σ_х М(Т)=0 D(T)=1

При центрировании полигон и функция плотности сдвигается влево на величину М(х), при стандартизировании сжимается относительно оси ординат в σ_х раз.

27. Дисперсия случайной величины. Её свойства. Отличия независимых и зависимых СВ в расчете дисперсии их суммы. Среднее квадратическое отклонение. Понятие о центрированной и стандартной случайной величине.

Дисперсия характеризует разброс, рассеяние значение СВ вокруг её мат. ожидания. Для дискретной СВ с конечным числом значений n , для СВ, принимающей бесконечное, но счетное число значений (если ряд сходится) . Дисперсия характеризует разброс, рассеяние значение СВ вокруг её мат. ожидания для непрерывной СВ

Свойства дисперсии:

1) D(C)=0

2) D(CX)=C^2*D(X)

3) D(X)=M(X²)-[M(X)]²

4) D(X±Y) = D(X)+D(Y) для независимых D(X±Y) = D(X)+D(Y) ±2cov(X,Y) для зависимых

5) D(XY)=D(X)*D(Y)+D(X)*(M(Y))²+D(Y)*(M(X))²

Среднее квадратическое отклонение

Центрированная СВ: ẋ=х-М(х) М(ẋ)=0 D(ẋ)=D(x)

Стандартная СВ: Т= ẋ/σ_х М(Т)=0 D(T)=1

28. Начальные и центральные моменты k-го порядка СВ, их наиболее применимые значения. Связь между ними.

Момент СВ – числовая характеристика распределения СВ. Начальный момент k-го порядка считается по формуле . ν₁=М(х); ν₂=М(х²) D(x)= ν₂ – (ν₁)²

Центральный момент k-го порядка считается по формуле μ_k(x)=M(X-M(X))^k = M(ẋ)^k

μ₁=0 μ₂=D(X) μ₃ = ν₃-3ν₂ν₁+2(ν₁)² – используется для расчета коэффициента асимметрии.

μ₄=ν₄-4ν₃ν₁+6ν₂(ν₁)²-3(ν₁)⁴ - используется для расчета коэффициента эксцесса.

29. Коэффициенты асимметрии и эксцесса СВ. Мода.

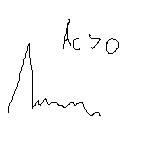
К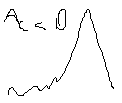оэффициент асимметрии с конечным 3м моментом – показатель асимметричности распределения, определяющий степень наклона полигона вероятностей дискретной случайной величины или скошенности функции плотности вероятностей непрерывной СВ.

Для симметричного распределения Ас=0.

Ас>0 – правосторонняя асимметрия

Ас<0 – левосторонняя асимметрия

Коэффициент эксцесса с конечным 4м моментом – показатель, служащий мерой

крутости (плосковершинности и крутовершинности) у кривой плотности вероятностей непрерывной СВ и у полигона дискретной СВ по сравнению с функцией плотности вероятности нормального закона распределения.

Мода – наиболее часто встречающееся значение СВ. Если одна мода, то распределение унимодальное, если 2 моды – бимодальное, много мод – полимодальное.