А) спектр амплитуд, б) спектр фаз сигнала

1.2. Спектры основных периодических сигналов

1. Спектр гармонического сигнала. Простейшим периодическим сигналом является гармоническое колебание s(t) = A_mcos(ω₀t+₀). Оно состоит из одной гармоники с амплитудой A_m и начальной фазой ₀, которые располагаются на частоте ω₀. Временная диаграмма, амплитудный и фазовый спектр гармонического сигнала приведены на рис. 1.2.

а)	 An  б) φ в)
Рис. 1.2. Детерминированный (гармонический) синусоидальный сигнал: a) временная диаграмма и его; б) амплитудный спектр; в) фазовый спектр

2. Спектральный состав прямоугольных видеоимпульсов

Рассчитаем амплитудный и фазовый спектры периодической последовательности прямоугольных видеоимпульсов, имеющих амплитуду u(В), длительность (с), период повторенияТ (с) и расположенных симметрично относительно начала координат (рис. 1.3а).

Определим среднее значение амплитуды видеоимпульса за период:

, (1.5)

г

S (t)

депринято называтьскважностью импульса, Т – период следования импульсов,   длительность импульсов.

t T  0 /2 -/2 U а)

б)

Рис. 1.3. Временная диаграмма и амплитудный спектр периодической последовательности прямоугольных видеоимпульсов

Так как исследуемая функция является четной, в ряде Фурье будут отсутствовать слагаемые с синусоидальной составляющей, т.к. . Следовательно, достаточно определить амплитуды косинусоидальных составляющих:

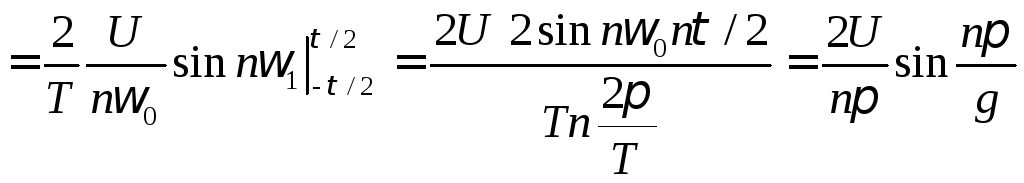. (1.6)

Из (1.5) и (1.6) следует, что среднее значение униполярного меандра равно амплитуде меандра деленной на скважность импульсов; амплитуды гармоник, кратные скважности (, k = 1, 2, 3,…), равны нулю. Например, если скважность равна 2, то в ряде Фурье будут присутствовать только нечетные гармоники . Ряд Фурье, аппроксимирующий периодическую последовательность видеоимпульсов, иметь вид:

, (1.7)

где .

На рис. 1.3б приведен амплитудный спектр сигнала при скважности g=4.

3. Треугольный импульс (симметричный).

Временная диаграмма сигнала приведена на рис.1.4а. Коэффициенты ряда Фурье рассчитываются по формулам:

–среднее, ,b_k=0.

Амплитудный спектр треугольного импульса приведен на рис.1.4б.

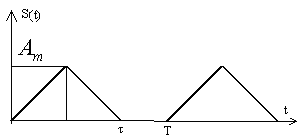
а) б)

Рис. 1.4. Треугольный импульс (симметричный) (а) и его спектр (б)

4. Треугольный импульс (пилообразный).

Временная диаграмма сигнала приведена на рис.1.5а. Коэффициенты ряда Фурье рассчитываются по формулам:

–среднее, , а_k=0.

Амплитудный спектр пилообразного импульса приведен на рис.1.5б.

а) б)

Рис. 1.5. Треугольный импульс (пилообразный) (а) и его спектр (б)

1.3. Модулированные сигналы

Сигналы, поступающие из источника сообщений (микрофона, передающей телевизионной камеры и т. д.), как правило, являются низкочастотными и не могут быть переданы по радиоканалу на большие расстояния.

При передаче по радиоканалу необходимо спектры этих сигналов перенести из низкочастотной области в область более высоких частот (радиочастот). Данная процедура в радиотехнике носит название модуляции.

Несущее или высокочастотное колебание генерируется в передающем устройстве, оно эффективно излучается антеннами и с малыми затуханиями распространяется в пространстве. В радиотехнике широкое распространение получили системы модуляции, в которых в качестве несущего используется простое гармоническое колебание s(t)=S_m Sin(₀t+₀). При изменении во времени одного из параметров несущего колебания (амплитуды, частоты, фазы) по закону передаваемого сообщения, несущее колебание приобретает новое свойство – нести в себе информацию, которая заложена в низкочастотное сообщении.

Т.о. модуляция это процесс изменения одного из параметров (амплитуды, частоты, фазы) высокочастотного (несущего) колебания по закону управляющего низкочастотного колебания.

Процесс обратный модуляции, при котором из модулированного сигнала извлекается низкочастотный сигнал, называется детектированием.

Рассмотрим наиболее простой вид модуляции – амплитудную модуляцию.

1.4.1. Амплитудная модуляция (АМ).При амплитудной модуляции (АМ) прямо пропорционально амплитуде информационного сигнала s(t) изменяется амплитуда несущего колебания , где–постоянная амплитуда высокочастотного колебания,– коэффициент пропорциональности:

,

где –постоянная угловая частота, –постоянная начальная фаза.

В общем случае s(t) носит случайный характер, но для выявления основных характеристикAM-колебаний будем полагать, чтоs(t) является детерминированной функцией и представляет собой чисто гармоническое низкочастотное колебание. Такой сигнал называется тональным, его спектр содержит одну гармоническую составляющую на частоте Ω.

Пусть , тогда аналитическое выражение АМ-сигнала имеет вид (временная диаграмма АМ-сигнала приведена на рис.1.6).

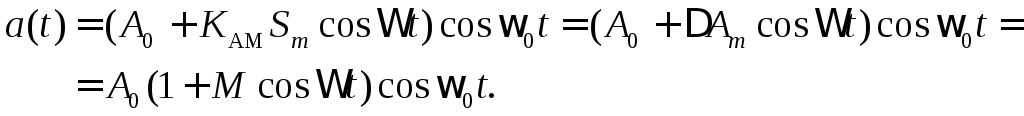(1.8)

Здесь ; , M – коэффициент, или глубина, модуляции.

Обычно ω₀>> Ω. Для неискаженной передачи: .

Спектр АМ-колебания легко определить, если записанное выражение (1.8), используя тригонометрические формулы, разложить на гармонические составляющие:

Рис. 1.6. Осциллограмма однотонального АМ колебания при МSупр(t)=1	Рис. 1.7. Спектр АМ сигнала при тональной модуляции.

На рис.1.7 представлен спектр АМ-колебания при модуляции гармоническим колебанием s(t). Он состоит из трех составляющих. Первое слагаемое представляет собой исходное немодулированное колебание (несущую) на частоте ω₀. Второе и третье слагаемые называются соответственно верхней ( на частоте – ω₀+Ω) и нижней (ω₀-Ω) боковыми составляющими. Если модуляция осуществляется сложным периодическим сигналом, спектр которого состоит из нескольких составляющих, то в спектре АМ-сигнала появляются верхняя и нижняя боковые полосы. Ширина спектра АМ-колебания равна удвоенной частоте от максимальной частоты модулирующего сигнала Ω_max, т.е. Δω = 2Ω_max.