Polnaya_uynya_shpora_po_sopromatu

8.2.4 Расчет на прочность при внецентральном сжатии

Расчет на прочность бруса из пластичного материала производят по наибольшему по абсолютной величине нормальному напряжению.

Условие прочности имеет вид:

R – расчетное сопротивление материала растяжения.

Для бруса из материала имеющего различные сопротивления растяжения и сжатия необходимо производить проверку прочности как по наибольшим растягивающим напряжениям, так и по наибольшим сжимающим напряжениям.

Rs – расчетное сопротивление материала на сжатие. x, y – координаты опасной точки.

Для сечения типа прямоугольных, двутавр и т.д. условие прочности может быть записано в виде:

Wx и Wy – моменты сопротивления сечений.

В приведенных формулах для расчета напряжений следует подставлять абсолютные значения M, Mx, My, x и y, а знак нужно принимать для всего слагаемого в целом, устанавливая его по характеру деформации стержня, имея в виду, что напряжение растяжения принимается со знаком «+», а сжатие «-».

На практике часто используют формулу для расчета напряжений, имеющую вид:

y и x – координаты точки, в которой определяется напряжение. yF и xF – координаты приложения силы.

При использовании этой формулы условие прочности имеет вид:

8.2.1 Внутреннее сжатие.Внутренние силовые усилия

.Если при растяжении/сжатии внешняя сила приложена в ЦТ сечения,то такое растяжение/сжатие наз.центральным.Если приложена не в ЦТ сечения,а с некоторым смещением,то такое сжатие/растяжение

8.3.1 Косой изгиб – такой вид изгиба, при котором сила действует к главным осям инерции под углом

Есть 2 вида косого изгиба:

1)Плоский

2)Пространственный

Плоский косой изгиб – хар-рен тем, что все нагрузки расположены в одной пл-ти, называемой силовой. Упругая линия деформ. Бруса яв-ся плоской кривой, но эта плоскость не совпадает с плоскостью действия нагрузки. Пространственный косой изгиб – возникает при действии на брус нагрузок, расположенный в разных плоскостях. В этом случае упругая линия изогнутого бруса является пространственной кривой

8.3.2 Определение косого изгиба.

При поперечном косом изгибе в поперечных сечениях бруса возникают и внутр. силовые факторы: поперечные силы(Qx Qy) и изгибающие моменты (Mx My). Влияние поперечных сил, как правило, незначительно и при расчёте на прочность и жёсткость не учитываются

9.1устойчивость стержней и общие сведения

Если прямой стержень,размеры которого слишком малы по сравнению с длинной сжим.небольшой силой,приложенной в центре тяжести сечения,то он будет испытывать только укорочение.Стержень находится в состоянии

устойчивого равновесия.По мере увелич.вертик.нагрузки стержень все медленнее возвращ.назад при его отклонении, и наступит такой момент,когда стержень не вернется в первонач.положение.состояние

безразличного равновесия. В таком сост.при дальнейшем

незнач.увелич.нагрузки наступает значит.деформ.стержня.Т.О,стержень проходит 3 стадии равновесия:устойчивое,безразличное и неустойчивое.Эти

состояния можно характеризовать так:Изгиб,связанный с потерей устойчивоси назыв.продольным,т.к. его вызывает продольная нагрузка.Значение продольной сжим.нагруз.,при которой стержень будет в сост.безразличн.равновесия(критичное сост.) назыв.критической силой.Состояние сжатого стержня при критич.силе рассматривается как предельное(опасное).В целях безопасой работы сжатых конструкций вводится коэф.запасов устойчивости,с помощью которого вычисляется безопасная нагрузка. Fmax=Fкр/n Значение коэф.запаса устойчивости принимается несколько большим,чем значение запаса прочности.Поскольку учитыватся такие небл-е условия работы сжат.стержня,как возможн.его начальная кривизна,отклонения силы от ц.т. сечения.

9.2Опрепеделине критической силы

В практ.расчетах для опр.критич.силы используют формулу Эйлера:Fкр=(П2*Е*Imin)/( μ*L)2

Е-модуль упругости, Imin-миним.из 2ух существ.моментов инерции,L-длина стержня, μ-коэф.приведенной длины стержня.Формула эйлера справедлива в предположении упругой работы стержня,хар-й законом Гука,поэтому она может бфть использована,когда критичное напряжение не превышает предел

пропорциональности. 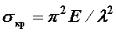-критич.напряжение,где -гибкость стержня,и минимальный радиус инерции сечений Для стержней из стали формула Эйлера применима,если гибкость равна 100 и более.Если гибкость будет меньше 100,формула неприменима,т.к.критичное напряжение будет больше предела пропорциональности.В этом случае для опр.критич.силы использ.формулу Ясинского: σкр = a – bλ+сλ2, где abcпостоянные,завис.от вида материала. Критич.сила определяется: Fкр = σкрA Если гибкость стержня менее 40,потеря устойчивости исключена и расчет ведут по условию прочности на сжатие.

9.3Практические расчеты стержней на устойчивость.

На практике расчет на устойчивость сжатых стержней ведут из условия устойчивости:

σmax=N/A<R*φ,где φ-коэф.продольного изгиба,зав-й от материала стержня и его гибкости.Приведенный расчет по внешнему виду напоминает обычный расчет на прочность про сжатии.Вместе с тем,это расчет на устойчивость,поскольку он включает коэф.продольного изгиба φ,учит.явление потери устойчивости.Приведенная формула позволяет выполнять три вида расчета:1)проверочный расчет.2)определение допустимой нагрузки(N=ARφ).3)подбор сечения элемента конструкции(A=N/Rφ)

Нагрузки, воздействующие на конструкции с большими или неравномерными скоростями, а также нагрузками внезапного кратковременного действия называются динамическими

при действии этих нагрузок появл-ся большие силы энергии, которые в расчетах необходимо учитывать. Установлено, что силы динамического воздействия пропорциональны статическим, поэтому расчет при динам. Нагрузках выполн. По методам разрешенных для статических нагрузок, но с введением динамического коэффициента.

Различают следующие виды расчетов на динамическую нагрузку

1.Расчет на действие сил инерции

2.Расчет на ударную нагрузку

3.Расчет на колебательную нагрузку

При поднятии груза с ускорением а ,на трос будут действовать вес груза σ и сила инерции

Fi

Где Nстпродольная сила в тросе при стат-ом положении груза

Ngпродольная сила в тросе при поднятии груза с ускорением а

g- Ускорение свободного падения

ударная нагрузка харкат. Таким взаим.движ. тел, при котором после их соприкосновения за малый промежуток времени происходит резкое изменение скоростей. Изменение скорости ударяющего груза за короткое время вызывает большую силу инерции.

В зав-сти от направления действия удара и места его приложения могут возникать различные виды деформации, в том числе и сложные деформации.

Если упругую систему (стержень. Балку) вывести из состояния равновесия, каким-либо внешн. воздействием, а затем убрать это воздействие, то система будет совершать колебания около положения статического равновесия, такие колебания называют свободными.

Они будут продолжаться до тех пор, пока сообщенная энергия полностью не израсходуется на работу, против сил внутреннего трения и сопротивления среды.

По виду деф-ции элемента конструкции различают:

1.Продольные (при растяжении-сжатии стержня)

2.Поперечные (при изгибе балки)

3.Крутильные –при кручении

Если на элемент конструкции будет действовать не разовая сила, а периодически повторяющееся ,то элемент конструкции будет совпадать вынужденные , с частотой ,с которой

10.1Понятия о динамических нагрузках

Динамические нагрузкинагрузки с большими скоростями . При действии динамических нагрузак появляются силы энергии которых необходимо учитывать в расчетах. Нахождения нагрузок выполняется методом введения динамического коэф.

Различают виды расчета нагрузок : на действия сил энергии ; на ударную нагрузку ; на калебательную нагрузку .

ударная нагрузка – взаимодействие движения тела при которм после их соприкосновения за малый промежуток времени происходит разное изм.скоростей

10.2 Расчет на вибрационную нагрузку

Если упругую систему вывести из сос-яния равновесия каким либо внешним воздействием а затем нужно убрать это воздействие то изм. Будет совершать колебания около положения статического равновесия такие колебания наз. Свободными .

колебания различают : продольные ; поперечные ; крутящие