Polnaya_uynya_shpora_po_sopromatu

3.1 Поперечная сила

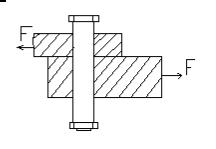
Деформацию сдвига можно представить на примере резки ножницами, когда две равные близкорасположенные силы направлены противоположно друг

другу и действуют на брус

перпендикулярно его продольной оси.

Рассечем брус сечением m-m, отбросим правую часть, а чтобы левая оставалась в равновесии заменим действие правой части на оставшуюся левой силой Q.

Тогда Σ Fy= - Q+F=0 Q=F

Когда сил несколько поперечная сила в сечении численно равна сумме сил действующих на оставшиеся части. Сдвиг, при котором в поперечном сечении действует только одна поперечная сила Q, называется чистым сдвигом.

§ 3.2 Касательное напряжение

Отношение поперечной силы Q к площади поперечного сечения A называется касательным напряжением.τ=Q/A – касательное напряжение, Па Касательное напряжение считается положительным,

если оно стремится повернуть бесконечно малый элемент конструкции походу часовой стрелки и наоборот. Касательное напряжение τ связано с нормальным напряжением δ зависимостью: p2=δ2+τ2, где p – полное напряжение Нормальное напряжение возникает в тех случаях, когда два сечения при деформации отдаляются друг от друга или наоборот сближаются. Касательное напряжение возникает при сдвиге одного сечения относительно другого. Иными словами, нормальное напряжение возникает при линейных деформациях, а касательное при условных. Считается, что касательное напряжение

равномерно распределяется по сечению. На взаимноперпендикулярных площадках касательное напряжение равно и противоположно по знаку, что обеспечивает равновесие элемента. Иными словами, касательные напряжения всегда действуют попарно (закон парности касательных напряжений). Они либо направлены к грани элемента (грани CK и AL) либо направлены от грани (грани

BE и DM).

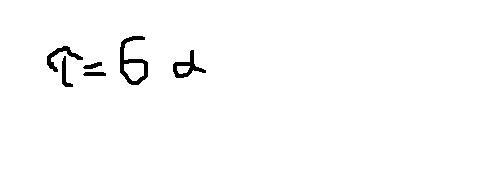
3.3 Закон Гука при сдвиге . Модуль упругости при сдвиге , связь

между модулями при сдвиге и растяжении .

При сдвиге считается что все волокна проворачиваются но одинаковый угол альфа.

где S – абсолютный сдвиг , l- длинна сдвигаемого участка .

Угол альфа называется относительным сдвигом , он характеризует величину деформации сдвига подобно тому как относительное удлинение характеризует деформацию растяжения.

Чем больше альфа тем больше касательное напряжение. Считают что она прямо пропорциональна :

G – модуль упругости при растяжении . Эта зависимость носит название Закон Гука для

сдвига.

G - определяется эксперементально .

3.4 Потенциальная энергия при чистом сдвиге.

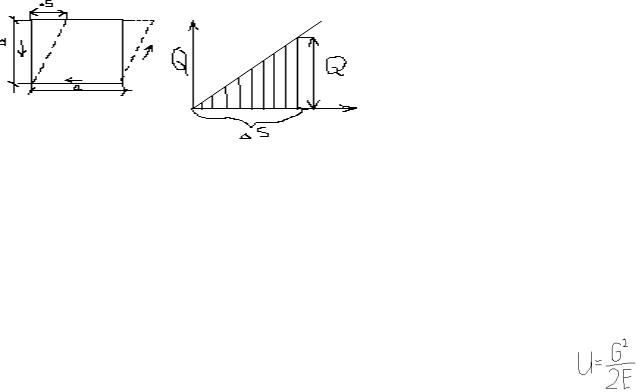
При деформации элемента ограниченного площадками чистого сдвига, работу совершает касастельная сила приложенная к верхней границе.касательная сила равна

Q= τ ∙a∙1 Τ=Q/A= Q|/a∙1

Сдвиг ∆S в пределах закона Гука пропорциональна силе Q поэтому работа этой силы W и численно равная ей потенциальная энергия U посчитана как заштрихованная на графике площадь w=U=1/2Q∙∆S или учитывая что Q= τA и ∆S=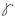 потенциальная энергия U=1/2 τ 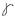a2 Объём элемента V=a2 ∙1

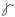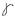Поэтому удельная потенциальная энергия деформации сдвига U=U/V=1/2 τ Применяя τ=G из этого следует, что = τ/G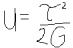

3.5. Расчёт на прочность и жёсткость при сдвиге.

Расчёт на прочность при сдвиге ведут из условия прочности при сдвиге:

τ мах = Qmax/A<[τ] , где τмах- макс. Касательное напряжение, [τ]-допуст. Касат. Напряжение.

Она определяется испытанием мат-ла либо принимается [τ]=0,6[δ]

Условие жёсткости при сдвиге: Smax=Q*a/A*G<[ΔS] ΔSmax-мах сдвиг при внешней нагрузки.

На практике расчёты на сдвиг чаще всего свод. к расчёту прочности мест соединения отдельных эл-ов конструкций. Соед. металлических эл-ов констр. осуществляется при помощи сварных швов, болтов и заклёпок. Деревянные констр. соед. врубок, шпанок и клея. Для соед. железобетонных констр. используют специальные закладные детали.

3.5.1. Расчёт сварных соединений.

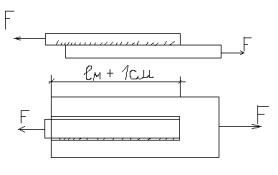
Рассмотрим соед. 2-х стальных листов в нахлёстку при помощи фланговых швов, подверженные действию растягивающих сил F.Под действием этих сил, листы по пл-ти соприкасаются, следовательно, произ. сдвиг относительно друг друга. Этому сдвигу препятствует угл. сварные швы. Считают, что разрушение шва происходит от касат. напряжений, путём среза(сдвига). При этом

касат. напр. принимают равномерно распределённым по площади среза. условия прочности сварного шва имеет вид: τмах=Q/A ≤[τ] или τмах=Q/l*h≤[τ] Q- поперечная сила, l-длина сварного шва. h-высота катета сварного шва. Обычно h принимают по констр. соображениям и из условия прочности находят расчётную длину шва, который из соображ. безопасности +1см. l=Q/h[τ] + 1см

3.5.2. Расчёт болтовых и заклёпочных соединений.

Рассмотрим болтовое соед. 2-х стальных листов. В практических расчётах считают,что соед. на болтах разрушается от среза на плоскости поперечного сечения. Если разрушение каждого болта происходит оп одной плоскости среза, такое соединение называется односрезным. Если по двум-двухсрезным ит.д.При расчёте на срез для упрощения принимают, что касат. напряж. в

поперечном сечении среза болта распределены равномерно по всей площади и все болты нагружены одинаково. Условия прочности болтового соед. : τмах= Q/Anm≤[τ], n- кол-во болтов, m-кол-во срезов Из этого условия определяем необходимое количество болтов, кот. обеспечат прочность болт. соед.: n=Q/Am[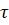]=4Q/Пd2m[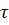] При недост. толщине соед. элементов может возникнуть их смятие в местах соприкосновения с болтом. Поэтому опред. дополнительно кол-во болтов из условия прочности соединения на смятие: σсмятие=F/dhn≤[

σсмятие]

Их данного условия определим кол-во болтов. Определение кол-во заклёпок в соед. осущ. аналогично в болтовом соед. Необходимо отметить, что наличие заклёпок или болтов вносит изменение в проверку прочности на раст. или сжатие самих листов. Опасным сечением каждого листа будет сечение, проходящие через заклёп. или болтовое соед.

3.5.3. РАСЧЕТ ВРУБОК

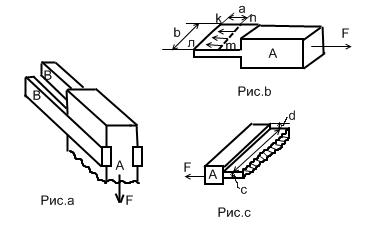
Пусть к неподвижным брусьям В при помощи врубки присоединен брус А, нагруженный силой F, приложенной по его оси.

Конец бруса А может разрушиться от скалывания по площади, равной удвоенной площади лmnk, величина которой равна А В(рис.b). Тогда расчет на скалывание ведут из условия

τ ск,max = Q/A ≤ [τ ск ] или

τ ск,max = Q/2ab ≤ [τ ск ] , где

Q=F,

[τ ск ] – допускаемое напряжение на скалывание (берут из справочника) Концы врубки испытывают напряжение смятия. Расчет на смятие ведут из уравнения:

σ см,max = F/2bd ≤ [σ см ] , где

[σ см ] – допустимое напряжение на смятие древесины (из справочника) Врубки также рассчитывают на разрыв в опасном сечении (заштрих. сечение на рис.с)

Площадь его равна bc.

Тогда расчетное уравнение на разрыв будет иметь вид: σ max = F/bc ≤ [ σ] ,

где [ σ] - допустимое напряжение на разрыв.

4.1. ГЕОМЕТРИЧЕТКИЕ ХАРАКТЕРИСТИКИ СЕЧЕНИЙ ОСНОВНЫЕ ПОНЯТИЯ.

При изучении растяжении сжатия прямых стержней было установлено, что сопротивление стержня пропорционально площади поперечного сечения: чем больше площадь поперечного сечения, тем меньше напряжение в сечении и меньше удлинение стержня. Картина резко меняется, если сила приложена к стержню перпендикулярно его оси, вызывая его изгиб.

Если на стержень, заделанный одним концом с поперечным сечением в виде вытянутого прямоугольника, действует сила, приложенная на другом конце, то стержень будет изгибаться, и сечение переместится на некоторую величину f1.

Если стержень повернуть на угол 90º вокруг его оси так, чтобы наибольший размер поперечного сечения

расположился горизонтально, то под действием той же силы конец стержня опустится на величину f 2, значительно большую, чем f1.

Таким образом, при одной и той же площади, в зависимости от ориентации поперечного сечения, стержень может по-разному сопротивляться одной и той же оси.

Следовательно, площадь поперечного сечения не может характеризовать в полной мере сопротивляемость стержня изгибу.

При изучении изгиба, а также кручении стержня, необходимо привлекать более сложные геометрические характеристики сечения.

4.2. СТАТИЧЕСКИЙ МОМЕНТ ПЛОЩАДИ ПОПЕРЕЧНОГО СЕЧЕНИЯ.

Предположим, что задано поперечное сечение стержня с площадью А, тогда статический момент этой площади относительно произвольных осей х и у, лежащих в одной плоскости с сечением А:

Sx = ∫ ydA; Sy = ∫ xdA dA – элементарная площадка с координатами х и у.

Если известны координаты центра тяжести всего сечения (хс и ус), то:

Sx = усА; Sy = хсА Статический момент имеет размерность м3 . Он в зависимости от положения фигуры относительно осей координат может быть положительным, отрицательным и равным 0.

Статический момент, относительно оси, проходящей через центр тяжести, равен 0, а такая ось называется центральной.

4.3. Определение центра тяжести плоского сечения Координаты центра тяжести плоской фигуры по отношению к принятым осям находят:

ус= Sx/A; хс= Sy/A Для фигуры, имеющей ось симметрии, центр тяжести находится на этой оси и определяется лишь одной координатой, если сечение имеет 2 оси симметрии, то центр тяжести соотв. их точке пересечения. Для сечения, состоящего из двух частей, центр тяжести находится на прямой, соединяющей центры тяжести этих частей. В случае сплошной фигуры, центр тяжести определяется по формулам: ус =∑ Sx/A хс =∑ Sy/A