Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский национальный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Pole

.pdf

Скачиваний:

Добавлен:

31.05.2015

Размер:

344.42 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

1) Скалярное поле определено функцией e	x 2 y 2 z 2 . Найти градиент поля в точке	A 1; 0; 1 .
Построить поверхности уровня для 1, e,	4 .

Определение. Градиентом скалярного поля u

grad u

;

x, y, z называется векторная функция

uz .

Смысл. Функция (скалярная функция) ≡ скалярное поле. Градиент функции ≡ скорость изменения функции в

конкретной точке; величина векторная.

Градиент функции есть вектор, направление которого указывает направление наибыстрейшего возрастания функции, а модуль равен наибольшей скорости изменения функции в определённой точке. Строго говоря, градиент является направленным отрезком (фиксирован в фиксированной системе координат, в то время как вектор (свободный вектор) есть класс эквивалентности направленных отрезков).

► В произвольной точке M x; y; z :

e x 2 y 2 z 2 x e

x 2 y 2 z 2

e x 2 y 2 z 2

x 2 y 2 z 2

e x 2 y 2 z 2

x e x 2 y 2 z 2

x 2 y 2 z 2

e x 2 y 2 z 2 y e

x 2 y 2 z 2

e x 2 y 2 z 2

x 2

y 2 z 2 y

e x 2 y 2 z 2

2 y

y e x 2 y 2 z 2

x 2 y 2

z 2

x 2 y 2 z 2

e x 2 y 2 z 2 z e

x 2 y 2 z 2

e x 2 y 2 z 2

x 2

y 2 z 2 z

e x 2 y 2 z 2

z e x 2 y 2 z 2

x 2 y 2

z 2

x 2 y 2 z 2

В точке A 1; 0; 1 :

1 e

12 0 2 1 2

12 0 2 1

0 e

12 0 2 1 2

12 0 2 1

1 e

12 0 2 1

Градиент скалярного поля x; y ; z

в произвольной точке M x; y; z :

grad

Градиент скалярного поля в точке A 1; 0; 1 :

e 2

grad

; 0;

► Поверхности уровня для 1, e, 4 .

а) При 1:

e x 2 y 2 z 2 1

x 2 y 2 z 2 0

- поверхностью уровня является точка 0; 0; 0 .

б) При e :

e x 2 y 2 z 2 e

x 2 y 2 z 2 1

- поверхностью уровня является сфера с центром 0; 0; 0 и радиусом r 1.

в) При 4 :

x 2 y 2 z 2	4
x 2 y 2 z 2	e ln 4

x 2 y 2 z 2 2 ln 2 2

- поверхностью уровня является сфера с центром 0; 0; 0 и радиусом r 2 ln 2 .

в точке A 1; 0;1

B 3; 2; 2 .

2) Найти производную функции arctg

в направлении

AB , где

x y

Производная функции x , y , z

по направлению a в точке A :

grad

1 ; 2 0 ; 2 1 2; 2;1

AB 3

► В произвольной точке M x; y; z :

arctg

x y

x y x

z x

		x	z

	arctg
y		z
			x y y
		x	z

	arctg

z		z	x y z

В точке A 1; 0;1 :

x y 2

x 2

x y

z 2 x 2

z 2

x y

z 2 x 2

z z

				1						1							1
				1						1							1
x	A		12 12						1	0 2							2


				1				1
y	A		1 0 2					1
y

			1						1					1
			1						1					1
z	A		1 0				12 12							2


Градиент скалярного поля x; y ; z																	в произвольной точке M x; y; z :
grad					i				j				k
grad					i				j				k
			x				y				z
Градиент скалярного поля в точке A 1; 0;1 :
grad																				1			1		1	;	1;	1


		A			x			i		y					j		z	k			i j			k
							A					A						A		2			2		2			2
																				2			2		2			2

► Производная функции x, y , z																в точке A 1; 0;1
► Производная функции x, y , z																в точке A 1; 0;1						по направлению a AB 2; 2;1 :
														1		2	1 2		1 1			1 2		1
			grad					AB																	5
			grad					AB
						A								2					2					2
a						A																	3		6
	A					AB									2 2 2 2 12
	A					AB									2 2 2 2 12

			x 2i y 2 j z 2k

3) Показать, что поле вектора a					является потенциальным. Найти его потенциал.
			x 3 y 3 z 3
Здесь P x; y ; z	x 2		Q x; y; z		y 2			R x; y ; z	z 2
		,					,			.
	x 3 y 3 z 3			x 3	y 3	z 3			x 3 y 3 z 3

► Векторное поле a P x; y; z i Q x; y; z j R x; y; z k называется потенциальным (безвихревым, градиентным), если во всех точках поля ротор равен нулю: rot a 0 .

rot a

P x; y; z

Q x; y; z

R x; y; z

x 2

y 2

z 2

x 3 y 3 z 3

z 2

3 y 2

y 2

3z 2

z 2

3x 2

x 2

3z 2

y 2

3x 2

x 2

3 y 2

- следовательно, поле вектора a потенциальное.

Найдём потенциал U векторного поля a по формуле

U x; y ; z

x, y, z

Pdx Qdy Rdz

x0 , y0 , z0

Выберем в качестве фиксированной точки точку с координатами 1; 0; 0

U x; y; z

x, y, z

x 2dx

y 2dy

z 2dz

0;0;0 x

Интегрируем по ломаной:

U x; y; z								x					x	2												y						y	2										z							z		2
													x											dx								y								dy										z						dz
												3		3			3							dx					3				3			3				dy								3				3			3	dz
												3	y	3	z		3												3		y		3	z		3												3		y		3	z		3
								1	x				y		z			y 0, z 0								0 x					y			z					z 0				0		x					y			z
x	dx			y			y 2dy						z			z 2dz												1			y	d x 3 y 3									1	z		d x 3 y 3 z 3
	dx						y 2dy									z 2dz								ln	x			1				d x 3 y 3									1			d x 3 y 3 z 3
	x					x	3	y				3			3	y		3		z		3		ln	x			3					x	3	y			3			3					x	3			y	3		z	3
							3					3		x	3			3				3												3				3									3				3			3
1			0										0	x																	0											0
ln		x			1		ln				x 3 y 3					ln			x 3				1 ln				x 3			y 3 z 3							ln			x 3 y 3									C


					3																		3
					3																		3
		x			1					x 3 y 3							1				x 3 y 3 z 3									C				1 ln					x 3			1 ln					x 3 y 3 z 3										C
ln							ln											ln



1					3								x 3				3							x 3 y 3										3								3									x 3
					3								x 3				3							x 3 y 3										3								3									x 3
	ln			x 3			y 3 z 3							C			- потенциал поля a .
	ln			x 3			y 3 z 3							C			- потенциал поля a .
3
3

► Векторное поле a называется соленоидальным, если во всех точках поля дивергенция (расходимость)

равна нулю: d iv a

0 .

x 2

y 2

d iv a

2x x 3 y 3 z 3 x 2

3x 2

2 y x 3

y 3 z 3 y 2 3 y 2

2z x 3 y 3 z 3 z 2 3z 2

x 3 y 3 z 3 2

x 4

2xy 3 2xz 3

2 yx 3 y 4 2 yz 3

2zx 3 2zy 3

z 4

x 3 y 3 z 3 2

x x 3 2 y 3 2z 3 y 2x 3 y 3 2z 3 z 2x 3 2 y 3 z 3 0

x 3 y 3 z 3 2

-следовательно, поле вектора a не является соленоидальным.

4)Определить векторные линии поля градиентов функции x 2 y 2 z 2 2x 2 y z .

Поле градиентов функции x, y , z - векторное поле grad .

Векторные линии векторного поля a P x; y; z i Q x; y; z j R x; y; z k описываются дифференциальными уравнениями векторных линий:


	dx		dy	dz
	P x; y; z		Q x; y ; z	R x; y ; z
или		Q x; y ; z
dy		Q x; y ; z

		P x; y; z
dx		P x; y; z
		R x; y; z
dz		R x; y; z
		P x; y; z

dx

-нормальная система дифференциальных уравнений относительно двух неизвестных функций y x и z x .

►Частные производные в произвольной точке M x; y; z :

x 2 y 2 z 2 2x 2 y z x 2x 2x

x 2 y 2 z 2 2x 2 y z y 2 y 2y

z x 2 y 2 z 2 2x 2 y z z 2z 1

Градиент скалярного поля x; y ; z в произвольной точке M x; y; z : grad x i y j z k 2x 2 ; 2 y 2 ; 2z 1

► Дифференциальные уравнения векторных линий:

dy	2 y 2
		2x 2
dx		2x 2
dz		2z 1
		2x 2
dx		2x 2

Видим, что система в данном случае распадается на два отдельных уравнения, содержащих каждое только одну неизвестную функцию. Интегрируем:

2 y 2

2x 2

2 y

2x 2

d 2 y 2

d 2x 2

2 y 2

2x 2

2 y 2

2x 2

2 y

2 C

2x 2

y C

1 1

2z 1

2x 2

d 2x 2

d 2z 1

2z 1

2x 2

ln 2z 1 ln 2x 2 ln C2

2z 1 C2 2x 2 z C2 x 1 21

Линии пересечения этих плоскостей и есть векторные линии поля градиентов данной функции:

y C1 x 1 1

z C2 x 1 12

Литература:

1) Аксёнов А.П. "Математика. Математический анализ", часть 2, 2005, стр. 739 (задача).

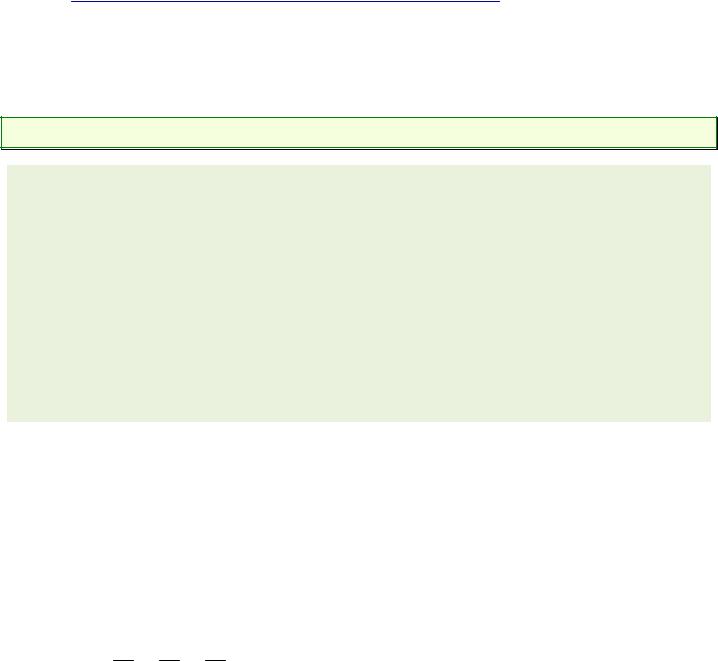
5) Вычислить криволинейный интеграл вектора a y 1 i x 2 j zk по дуге окружности

x a

y a cos tz a sin t

лежащей в первом октанте от точки A a; a; 0 до точки B a; 0; a .

Криволинейный интеграл 2-го рода от вектор-функции a ax i ay j az k		по кривой AB обозначается
a dr ax x, y , z dx ay x, y , z dy az x, y , z dz
AB	AB
и в случае параметрического задания кривой интегрирования
x x t
	t
y y	t

z z t

вычисляется по формуле

ax x, y , z dx ay x, y , z dy az x, y , z dz

ax x t ; y t ; z t x t ay x t ; y t ; z t y t az x t ; y t ; z t z t dt

(результат интегрирования зависит от направления интегрирования)

Вданном случае путь интегрирования проходим при изменении параметра 0 t 2 , следовательно

y t ;

z t x

ay x t ; y t ; z t y

t az x t ; y t ; z t z

t dt

ax x t ;

sin t

sin

0 a 2 a sin t a sin t a cos t dt a

2t dt

a 2 cos t

a 2

cos 2t

a 0

Литература:

1)Краснов М.Л., Киселёв А.И., Макаренко Г.И., Шикин Е.В., Заляпин В.И. "Вся высшая математика", том 4, 2005, стр. 49;

2)Письменный Д.Т. "Конспект лекций по высшей математике", 2005, стр. 407.


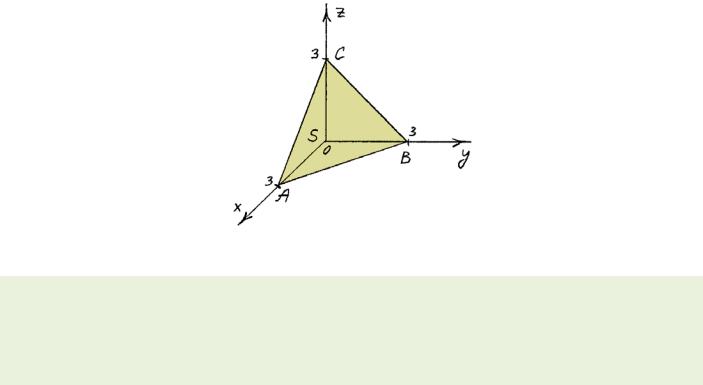
6) Вычислить поток вектора a y x i y z j x z 2 k через:
а) полную поверхность пирамиды, вершины которой S 0; 0; 0 ,	A 3; 0; 0 ,	B 0; 3; 0 ,	C 0; 0; 3 ;
б) грань ASC в положительном направлении оси Oy .

Вычислим поток векторного поля a через полную поверхность пирамиды непосредственно (по определению) и применяя формулу Остроградского.

1-й способ решения - по определению.

Поток вектора (векторного поля) a P;Q; R можно вычислить как поверхностный интеграл

П Pdy dz Qdx dz Rdx dy

где P P x; y; z , Q Q x; y; z , R R x; y; z - проекции вектора a на соответствующие координатные оси.

Решая таким способом, в процессе решения получим ответ на пункт "б".

Рассмотрим четыре составляющие потока П ПASB ПBSC ПASC ПABC и вычислим их методом проектирования на одну из координатных плоскостей.

Нормальный вектор к поверхности ASB :										n k . Рассматриваем проекцию на плоскость xOy , поэтому
z 0 :							y x i y z j x z 2 k k d

ПASB		a n0 d																	x 0 2 dx dy
	ASB					ASB												ASB
		3	x 3			0					0				0
	dx				x dy dx x y				0 x 3		x 3 x dx 3x x 2						dx
																	dx

		0	0			3					3				3
		3x	2	x	3	0		3 3		2	3 3	3	1	1		3 3	3 2
		3x	2	x	3	0		3 3		2	3 3	3	1	1		3 3	3 2
							0				3							4, 5
							0				3							4, 5
		2		3		3		2			3		3	2		6	2
		2		3		3		2			3		3	2		6	2
Нормальный вектор к поверхности BSC :										n i . Рассматриваем проекцию на плоскость yOz , поэтому
x 0 :		a					y x i y z j x z 2 k i d
																			y 0 dy dz
ПBSC			n0 d																y 0 dy dz
	BSC					BSC												BSC
		3	y 3			0					0				0
	dy				y dz dy y z				0 y 3 y 3 y dy 3 y y 2 dy 4, 5


		0	0			3					3				3

Нормальный вектор к поверхности ASC : n j . Рассматриваем проекцию на плоскость xOz , поэтому

y 0 :		a									y x i y z									j x z 2 k j d

ПASC				n0 d																						0 z dx dz
	ASC								ASC																	ASC
	3			x 3					3			z	2		x 3		1	3		3 x 2 dx 1				0
	3			x 3					3				2		x 3			3						0
	dx					z dz dx																		3 x 2 d 3 x
	dx					z dz dx																		3 x 2 d 3 x
	0				0				0		2				0		2	0					2	3
											2				0		2						2

	1		3 x 3					0			1		3	0 3		3 3				3		3 3	3 2		4, 5
			3 x 3																				3 2

	2				3			3		6												6	2
	2				3			3		6												6	2
																	F		;	F	;	F	1;1;1 , т.к.			F x, y , z x y z 3 .
Нормальный вектор к поверхности ABC : n																	x		;	y	;		1;1;1 , т.к.			F x, y , z x y z 3 .
																	x			y		z
		1			1		1
Нормируем: n				;		;			(для метода проектирования на одну из координатных плоскостей нормаль
Нормируем: n		3		;	3	;	3
		3			3		3

необязательно нормировать). Рассматриваем проекцию на плоскость xOy , на рассматриваемой поверхности

z 3 x y :

ПABC		a n0 d		y x dy dz			y z dx dz				x z 2 dx dy
	ABC		BSC			ASC				ASB
	3	y 3		3	x 3			3	x 3	x z 2	dy
dy			y x dz dx			y z dz dx				x z 2	dy
	0	0		0	0			0	0
	3	y 3			3	x 3				3	x 3	x 3 x y 2	dy
dy			y 3 y z dz dx				3 x z z dz dx					x 3 x y 2	dy
	0	0			0	0				0	0
3	y 3		3	x 3			3	x 3	x 2 y 2 2xy 5x 6 y 9 dy				45
dy		3 z dz dx			3 x dz dx				x 2 y 2 2xy 5x 6 y 9 dy				45	11, 25
0	0		0	0			0	0					4
0	0		0	0			0	0

Следовательно

П ПASB ПBSC ПASC ПABC 4, 5 4, 5 4, 5 11, 25 6,75

Ответ:

а) поток вектора a через полную поверхность пирамиды П 6,75 ;

б) поток вектора a через грань ASC в положительном направлении оси Oy ПASC 4, 5 .

► Вычисление потока поля через замкнутую поверхность по формуле Остроградского.

Теорема Остроградского (Остроградского-Гаусса, Гаусса-Остроградского).
Если в некоторой области G пространства R 3 координаты вектора
a P x, y , z i Q x, y , z j R x, y , z k
непрерывны и имеют непрерывные частные производные P ,	Q ,	R	, то поток вектора (векторного поля) a
x	y	z

через любую замкнутую кусочно-гладкую поверхность S , лежащую в области G , равен тройному интегралу
от дивергенции этого поля по области V , ограниченной поверхностью S :
				0
П a	ds div a dv		(здесь ds n		d )
S		V

							P			Q	R		1 1					2z dv 2 z dv
П div a dv							x			y	z	dv	1 1					2z dv 2 z dv
	V			V			x			y	z				V							V
	V			V											V							V
	3	x 3	3 x y							3	x 3			z 2			3 x y	3	x 3
	3	x 3	3 x y							3	x 3						3 x y	3	x 3
2 dx dy					z dz 2 dx							dy						dx 3 x y 2 dy
2 dx dy					z dz 2 dx							dy	2				0	dx 3 x y 2 dy
	0	0	0							0	0							0	0


	3	x 3					2	d	3 x y			3				3 x y 3				x 3
	3	x 3					2					3				3 x y 3				x 3
dx 3 x y												dx					3			0
	0	0										0


		3															3					3
	1	3 x x 3 3 3 x 0 3 dx													1		3 x 3 dx				1	3 x 3 d 3	x
	3	0													3		0				3	0
		0															0					0
	1	3 x 4		3			1			3 3	4 3 0				4 3 3			6,75
	1	3 x 4					1

	3	4		0		12											4
	3	4		0		12											4

Ответ: поток вектора a через полную поверхность пирамиды П 6,75 .

Литература:

1)Краснов М.Л., Киселёв А.И., Макаренко Г.И., Шикин Е.В., Заляпин В.И. "Вся высшая математика", том 4, 2005, стр. 79, стр. 85 (пример 1);

2)Письменный Д.Т. "Конспект лекций по высшей математике", 2007, стр. 511.

7)Проверить формулу Стокса для поля вектора a 4x 2 x 2 z i y j 4z 2k , принимая за контур интегрирования - окружность

x 2 z 2 9

y 1

а за поверхность - часть поверхности цилиндра

x 2 z 2 9

1 y 5

и плоскость y 5 .

1 / 21 2 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
26.04.2019392.7 Кб13Philosophy.doc
#
02.08.201973.97 Кб80Physics.docx
#
31.05.2015278.53 Кб9Pip_-_gotovye_shpory.doc
#
26.03.20165.08 Mб9Places, Streets and Movement to Manual for Streets.pdf
#
15.04.201990.62 Кб4pl_lek.doc
#
31.05.2015344.42 Кб5Pole.pdf
#
31.05.2015135.38 Кб24politologia.docx
#
31.05.2015227.75 Кб136Politologia.docx
#
30.08.201929.08 Кб7Politologia.docx
#
26.03.20162.08 Mб23Polnaya_uynya_shpora_po_sopromatu.pdf
#
31.05.2015311.81 Кб18POS-terminaly_POS-sistemy.doc