
Polnaya_uynya_shpora_po_sopromatu
.pdf6.7Расчет балок на прочность
Взависимости от поставленной цели производят 3 вида расчетов:
1)проверка дополнительного напряжения в балке при известных размерах поперечного сечения и заданных прочностных характеристиках материала.
2)Подбор сечения, т.е. определения необходимых размеров поперечных сечений при заданных его форме и прочности характеристиках материала.
3)Определение предела нагрузки при заданных размерах сечения и характеристиках материала.
Расчеты балок производятся по наибольшим норм., касательных и эквивалентным (средневзвешенных) напряжениям.

6.7.1. Расчет на прочность при максимальных нормальных напряжениях.
Балки из пластичного материала изготавливают симметричного сечения для того, чтобы раст./сжим. Напряжения крайних волокон были одинаковы. Опасным сечением балки будет то сечение, в котором возникает мах изгибающий момент, а опасными точками этого сечения – наиболее удалённые от нейтральной оси. Условие прочности в опасном сечении без учёта знака изгибающего момента выглядит σмах= ≤[σ], Или для симметричного сечения σмах=
≤[σ], Или для симметричного сечения σмах=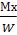 ≤[x], ,где W – осевой момент сопротивления поперечного
≤[x], ,где W – осевой момент сопротивления поперечного
сечения, м3. Wx=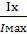 , Wx – геом. характеристика прочности поперечного сечения
, Wx – геом. характеристика прочности поперечного сечения
балки, чем больше момент сопротивления, тем меньше напряжение, |
|
возникающее в опасных точках. Осевой момент связан с полярным |
|
зависимостью Wρ=2Wx/ Для подбора сечения большая величина |
|
требуемого момента сопротивления определяется по формуле Wx тр= |
, |
τmax=Mo/Wx≤ . По полученным значениям Wx тр при заданной форме поперечного сечения подбирают размеры этого сечения. Определение предельной нагрузки определяется : Мx max=Wx . После расчёта балки по нормальным напряжениям производят проверку на прочность по наибольшим касательным напряжениям. На касательное напряжение необходимо проверять, когда сечение имеет резкое изменение ширины. Условие прочности имеет вид: τмах =(Q /b)/(Sx/Ix)≤ c , где с – расчетное сопротивление на срез. Расчет на прочность по эквивалентным напряжениям. Мах касательное напряжение возникает на уровне нейтральной линии, где нормальное напряжение =0. Наиболее напряженными являются промежуточные волокна, в которых возникают и те и другие напряжения. Здесь поперечная сила и изгибающий момент одновременно достигают больших значений . А также в сечениях с резко меняющейся шириной. При указанных сочетаниях нужна проверка: эквивалентных напряжений. Условие прочности : σэкв мах= ≤ 6.8Расчет балок на жесткость. Наряду с расчетом на прочность балку
≤ 6.8Расчет балок на жесткость. Наряду с расчетом на прочность балку
рассчитывают на жесткость. Даже весьма прочная балка может оказаться
l
непригодной, если под нагрузкой они сильно деформируются. Условие:

 , f – абсолютное значение стрелы прогиба. fн – значение стрелы
, f – абсолютное значение стрелы прогиба. fн – значение стрелы
прогиба, установленное. Помимо линейных перемещений сечение балки испытывает гловое перемещение. Существует несколько способов для определения углового и линейного перемещения. Опред-е линейного перемещения при помощи диф. уравнения изогнутой оси балки. Определение оси при помощи интеграла Бора Метод начальных параметров.В методе начальных параметров используют 2 уравнения: 1-е для определения прогиба; 2-е для определения углов поворота.
EIy=EIyo=EIQz+ |
+ |
+ |
(a) Диф-руя уравнение (а) по |
|
dz, получают выражение для |
определения углов поворота поперечного |
|||
сечения. |
|
|
|
|
|
|
EIQ=EIQ0+Mi(zi-ai)+ |
+ |
(b) |
7.1 Виды напряженного состояния
Через любую точку элемента конструкции можно провести большое кол-во различно ориентированных в пространстве сечений. Напряжения по каждой из этих площадок будут различны . Совокупность напряжений по всевозможным площадкам , проведенным через точку хар-т напряжение состояния в этой точке. Если в окрестности точки выделить элемент в виде бесконечно малого куба , то на его гранях будут действовать внутренние силы , заменяющие действие отброшенной части. Полное напряжение на гранях куба от этих внутренних сил будут состоять из нормальных и касательных напряжений.
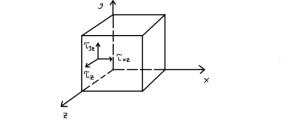 На невидимых гранях куба возникают такие же напряжения , но противоположном направленные.
На невидимых гранях куба возникают такие же напряжения , но противоположном направленные.
В нормальном напряжении присваивают индекс , указывающий ось , параллельно которой они направлены. Для обозначения касательных напряжений используется двойной индекс ; первый указывает ось, II которой направлено нормальное касательное напряжение ; второй указывает ось, II которой направлена нормаль площадки где действует нормальное напряжение.
При изменении ориентации грани призмы также меняются . И может оказаться , что касательное напряжение равно 0, а нормальное напр. в этом случае будут экстремальны . Такие площадки называются главными . А нормальное напряжение на них главным напряжением.
В общем случае нагруженные через любую точку можно провести три взаимно перпендикулярные главные площадки . Главные напряжения обозначают 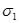 ,
,  ,
,  . При этом индексы следует расставлять так, чтобы выполнялось неравенство
. При этом индексы следует расставлять так, чтобы выполнялось неравенство
 >
> >
>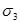 .
.
Если отличны от нуля все три главных напряжения, то напряженное состояние называется трехосным или объемным.
Если равно нулю одно из главных напряжения, то напряженное состояние называется двухосным или плоским.
Если равно нулю два главных напряжения, то напряженное состояние называется одноосным или линейным.

7.2 Линейное напряженное состояние
Q A
N sin
A
cos
2
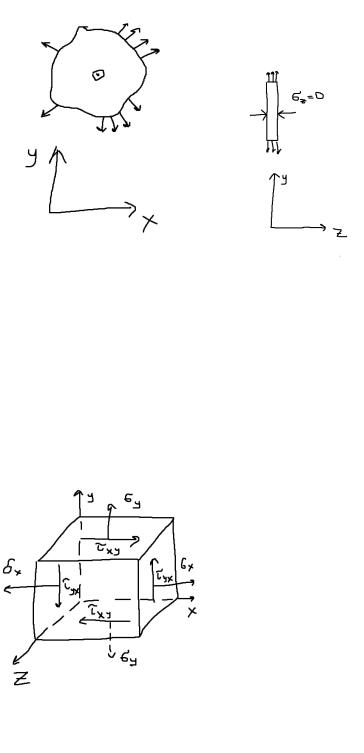
Примером линейного напряженного состояния является напряжение в стержнях испытываващих растяжение, либо сжатие. При растяжении силойF в его поперечном сечении.σ=N/A Касательное напряжение в этой площадке =0. Рассмотим сейчас не перпердикулярные оси площадку, а
наклоненную к ней под углом α. А/Аα=cosα |
|
||||||||||
Аα=A/cosα |
|
Любой площадку Аα внешняя |
|
||||||||
нормаль, которая образует с направлением |
|
||||||||||
силыF угол α. Нормальное и касательное |
|
||||||||||
sin 2 напряжение можно посчитать |
|
||||||||||
|
N |
|
N cos |
|
2 |
|
2 |
|
|||
|
|
|
|
|
|
cos |
|
|
0σα=σcos α (1) |
τα=σsin2α/2 |
|
A |
|
A |
|
|
|||||||
cos
(2)
Используя эти формулы проанализируем линейное напряжение состояние: 1) при α=0: (сos2α=1, sin2α=0) 0 max 0 0
Нормальное напряжение мах, а касательное =0. 2) при α=900: (сos2α=0, sin2α=0)
900 0 900 0
Т.е. в продольных сечение отсутствуют и нормальные и касательные напряжения. Это значит, что продольные элементы бруса по боковым поверхностям друг с другом не имеют никакого внутреннего силового взаимодействия и растяжение бруса можно уподобить растяжению пучка несвязанных друг с другом параллельных нитей. Как было отмечено площадки на которых нет касательных напряжений – это главные площадки, а нормальные напряжения на них – главные напряжения. Следовательно при осевом растяжении – сжатии главные площадки во всех точках бруса перпендикулярны его продольной оси, а нормальное напряжение в поперечном сечение – естьглавное напряжение. Обозначим его через σ1.
σ1=N/A Так как в данном случае отличные от 0 только одно главное напряжение, то рассматриваемое напряженное состояние является линейным или одноосным.
3) Как свидетельствует из формул (1) и (2) в других сечениях отличных от поперечных и продольных есть и нормальные, и касательные напряжения.
0Касательное напряжение максимально при α=450 (sin2α=1): 450 max 2 (3)
Минимально алгебраическое значение касательного напряжения при α=1350 (sin2α=-1): 1350 min 2 (3а)Из выражений (3) и (3а) видно, что наибольшее и наименьшее касательное напряжение равны по абсолютному значению и противоположны по знаку. Это свойство справедливо для любой пары касательных напряжений действующих по двум взаимно перпендикулярных сечениях.
7.3 Плоское напряженное состояние
Рассмотрим тонкую пластинку , нах-ся под действием произвольных к кромке пластины и лежащие на плоскости.
Так как на внешней поверхности пластины напряжение отсутствует и толщина пластины мала ,
то можно предположить что их нету и внутри пластины, на площадках II этой поверхности.
Вырежем куб из пластины в окрестности произв. точки К , сечениями перпендикулярными плоскости пластины.
Со стороны среды на куб будут действовать как нормальные , так и касательные напр..
При изучении плоского напр. состояния выделенного вокруг точки принято изображать в виде квадрата представляющего собой проекцию куба на плоскость , совпадающую с площадкой , на которой нет напряжения

Значение напряжений достаточно указать на 2-х взаимно перпендикулярных гранях.
Если требуется показать , возникающее не в одной паре взаимно перпендикулярных площадок , проходящих через данную точку , а в нескольких, то соответствующие квадраты изображаются как на рис с верху.
Если по граням куба действует главное напряжение 1, 2 , то определить нормальное и кас.
напряжение на площадках под углом a можно по формулам:
a= 1*cos2a+ 2*sin2a
|
|
|
1 |
2 |
sin 2 |
|
|
2 |
|||
|
|
|
|
||
|
|
|
|
|
Если на площадках действует не главное напряжение , то напр-е главных площадок определяют:
А численные значения главных направлений на этих площадках:

8.2.2. Нормальные напряжения при нецентральном сжатии.
Согласно принципу независимости действия сил нормальные напряжения в поперечном сечении равны алгебраической сумме напряжений от каждого внутреннего силового фактора.
|
|
|
|
|
|
|
N |
|
M X |
y |
M Y |
x |
N |
Мх |
My |
|
|
|
|||||||
|
|
|
|
A |
|
I X |
|
IY |
||||
|
|
|
|
|
|
|
|
|
||||
х и у – координаты точки, в которой определяется нормальное напряжение. Рассмотрим наиболее простой случай, когда сжимающая сила лежит в плоскости,
проходящей через ось симметрии или через главную ось инерции сечения.
В центр сечения приложим 2 противоположнонаправленные силы F’ и F’’ по величине равные F. Силы F’ и F’’ взаимно уравновешивают друг друга. Поэтому равновесие конструкции и условие работы не изменяются. Тогда силы F и F’’ составляют
пару сил, которые изгибают столб.
MY F C
Оставшаяся сила F’ производит сжатие колонны. В каждом поперечном сечении нормальное напряжение от сжатия распределено равномерно по всему сечению. Напряжение от изгиба на оси Y (нейтральной) равно нулю и возрастает по мере удаления от этой оси. При суммировании напряжений в зависимости от расстояния С, на котором сила приложена от оси Y, возможны 3 случая:
1) Напряжение от изгиба больше напряжения от сжатия.
N M , в этом случае в одной части сечения будут растягивающие, а в другой сжимающие напряжения (рис. а). Нейтральная ось сместилась, но проходит через сечение.
2) Напряжение от изгиба равно напряжению сжатия (рис. б).
N M , в этом случае нейтральна ось проходит по краю сечения , по всему сечению напряжение одного знака.
3) Напряжение от сжатия по абсолютной величине превышает наибольшее напряжение от изгиба: N M , нейтральная ось вне сечения.
При перемещении силы в центр тяжести нейтральная линия сместится в бесконечность.
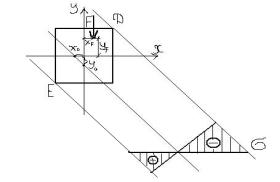
8.2.3. Определение опасных точек сечения.
Для нахождения опасных точек сечения определяется положение нейтральной линии и отыскиваются наиболее удаленные от нее точки, в которых и будут возникать наибольшие нормальные растягивающие и сжимающие напряжения.
Поскольку на нейтральной линии напряжение равно нулю, то уравнение нейтральной линии можно получить, если при равнять к нулю формулу нормальных напряжений:
|
N |
|
|
|
|
M X |
|
y |
|
|
|
|
|
MY |
x |
|
|
|
0 |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||||||||||||||||||||||||||
|
A |
|
|
|
|
I X |
|
|
|
|
|
|
|
|
|
|
|
|
IY |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Хо и Уо – текущие координаты точек нейтральной линии. |
||||||||||||||||||||||||||||||||||||||||||||||
Поскольку: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
M X F yF |
|
|
|
|
|
|
|
|
|
|
|
|
|
MY F xF |
|
||||||||||||||||||||||||||||||
N=F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
F |
|
F yF y0 |
|
F xF x0 |
|
0 |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
A |
|
|
|
|
|
|
|
I X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
IY |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
F |
|
|
|
|
|
y |
F |
|
y |
0 |
|
|
|
|
|
|
x |
F |
|
x |
0 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
A |
|
|
|
|
|
|
I X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
IY |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
I X |
|
i |
2 |
; |
|
IY |
|
|
i |
2 |
|
|
- радиусы инерции поперечного сечения относительно главных центральных |
||||||||||||||||||||||||||||||||
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
A |
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
осей. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
yF y0 |
|
|
|
xF x0 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Тогда: |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
||||||||||||||||||||
|
A |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iX |
|
|
|
|
|
|
|
|
|
|
iY |
|
||||||||||
Т.к. F/A≠0, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
y |
F |
|
y |
0 |
|
|
|
|
|
|
|
x |
F |
|
x |
0 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
0 |
|
|||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
iX |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iY |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
При |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
y0 |
0 x0 |
|
|
|
|
|
y |
|
|
Определив положение нейтральной линии, определяем |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
xF |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нормальные напряжения в наиболее удаленных от нее точках и |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||
|
|
|
|
|
|
|
|
x0 0 y0 |
|
|
iX |
|
|
строим эпюры.Поскольку нейтральная (нулевая) линия делит |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
yF |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сечение на две части, сжатую и растянутую, проводя к контуру |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
сечения касательные параллельные нейтральной линии.
Е и Д – точки, в которых будут действовать наибольшие сжимающие (Д) и растягивающие (Е) напряжения.
