9_Ломтадзе В.В., Шишкина Л.П_Практическая информатика_2011

Контрольные вопросы к главе 3

Способы измерения количества информации; что такое данные, что такое бит, байт, в каких единицах исчисляются

объемы данных; что такое система кодирования, система счисления, позиционная система

счисления; запись содержимого полубайта в десятичной, шестнадцатеричной и дво-

ичной системах; кодирование текста;

кодирование целых чисел, обратный и дополнительный код; кодирование действительных чисел, как складываются действительные

числа на регистрах арифметического устройства процессора; кодирование графической информации, векторная и растровая графика; кодирование аудио- и видеоинформации.

31

4. МОДЕЛИ И АЛГОРИТМЫ. РОЛЬ МОДЕЛИРОВАНИЯ И АЛГОРИТМИЗАЦИИ В РЕШЕНИИ ЗАДАЧ И ФОРМАЛИЗАЦИИ ЗНАНИЙ. ИНФОРМАЦИОННЫЕ РЕСУРСЫ

4.1. Модели решения вычислительных и функциональных задач

Человек всегда стремился понять, а значит представить с упрощением, доступным для своего понимания, многие процессы, явления и объекты. Так появились описательные модели (гелиоцентрическая модель Коперника), физические модели (глобус), картографические модели (карта), математические модели (уравнение плоскости), табличные модели (таблица "Объекты - свойства"). Но в наше время, во время очередной информационной революции (четвёртой

– после письменности, книгопечатанья и электричества) моделирование стало методом исследований, причём современное моделирование не мыслимо без компьютеров. В какой последовательности решаются исследовательские задачи

спомощью моделирования?

1)В области некоторой практической деятельности (предметная область) очерчивается круг актуальных задач, и рассматриваемые в этих задачах объекты, процессы и явления описываются набором параметров. Этот набор параметров (свойств, данных) подбирается так, чтобы можно было решать с достаточной для практики точностью и детальностью именно поставленные задачи. Для решения других задач будет другая модель тех же объектов, т.е. описание их другими параметрами. На этом же этапе решаются основные вопросы организации данных: где, в каких форматах (база данных, книга электронных таблиц, файлы прямого доступа или последовательные и т.п.) будут храниться исходные, промежуточные данные и результаты решения задач.

2)Известные и неизвестные параметры модели связываются математическими выражениями (линейные, нелинейные, дифференциальные и пр. уравнения, целевые функции и т.п.) – так строится математическая модель. Её коренное (философское) отличие от модели объекта или процесса состоит в том, что она может быть инвариантна к предметной области. Например, математическая модель линейного программирования применяется и при выборе оптимального плана выпуска продукции, и при решении обратных задач геофизики (уточнение параметров геологического объекта, по измеренным значениям создаваемого им магнитного, гравитационного или другого физического поля) и во многих других областях. Реализованная на компьютере математическая модель называется компьютерной математической моделью, а проведение целенаправленных расчетов с помощью компьютерной модели называется вычислительным экспериментом.

3)Выбираются аналитические и численные математические методы для оценки неизвестных параметров модели, разрабатываются алгоритмы для решения актуальных задач предметной области, причём с оценкой точности результатов, их однозначности и устойчивости.

32

4)Создаётся приложение – многофункциональная программа, состоящая

восновном из событийных процедур. Каждая событийная процедура обычно соответствует одному из пунктов меню и позволяет решать одну из задач.

Таким образом, модель – это искусственно созданный объект, дающий упрощенное представление о реальном объекте, процессе или явлении, отражающий существенные стороны изучаемого объекта с точки зрения цели моделирования.

Модель позволяет понять явление, структуру изучаемого объекта. Не построив модель, вряд ли удастся понять логику действия той или иной сложной системы, объяснить её действие, причины явлений и характер взаимодействия составляющих.

Задачи, которые мы решаем, по своему назначению можно разделить на две категории:

•вычислительные задачи, целью которых является определение некоторой величины;

•функциональные задачи, предназначенные для создания некоего аппарата, выполняющего некоторые функции.

Компьютерное моделирование включает несколько этапов:

Первый этап – определение целей моделирования. Эти цели могут быть различными:

•Понимание – модель нужна для того, чтобы понять, как устроен конкретный объект, какова его структура, основные свойства, законы развития и взаимодействия с окружающим миром;

•Управление – модель нужна для того, чтобы научиться управлять объектом или процессом и определить наилучшие способы управления при заданных целях и критериях;

•Прогнозирование – модель нужна для того, чтобы прогнозировать последствия способов и форм воздействия на объект.

Второй этап – определение входных и выходных параметров модели; разделение входных параметров по степени важности влияния их изменений на выходные.

Третий этап – построение математической модели. На этом этапе происходит переход от абстрактной формулировки модели к формулировке, имеющей конкретное математическое представление.

Четвертый этап – выбор метода исследования математической модели. Чаще всего здесь используются численные методы, которые хорошо поддаются программированию. Как правило, для решения одной и той же задачи подходит несколько методов, различающихся точностью, устойчивостью и т.д. От верного выбора метода часто зависит успех всего процесса моделирования.

Пятый этап: разработка алгоритма, составление и отладка программы для

ЭВМ.

33

Шестой этап: тестирование программы. Работа программы проверяется на тестовой задаче с заранее известным ответом. Обычно тестирование заканчивается тогда, когда пользователь по своим профессиональным признакам сочтет программу верной.

Седьмой этап: вычислительный эксперимент, в процессе которого выясняется, соответствует ли модель реальному объекту или процессу. Модель достаточно адекватна реальному процессу, если некоторые характеристики процесса, полученные на ЭВМ, совпадают с экспериментально полученными характеристиками с заданной степенью точности. В случае несоответствия модели реальному процессу возвращаемся к одному из предыдущих этапов.

Моделирование применяется для решения самых разных задач. Поэтому классификации моделей также разнообразны. Модель может быть статическая или динамическая (без учёта или с учётом изменений параметров во времени), детерминированная или стохастическая (надо найти определённые оценки параметров или распределения вероятностей), с обратной связью или без (актуально для динамических моделей). Что касается понятий "Информационное моделирование" и "Инфологическая модель", то эти термины скорее относятся к технологии проектирования баз данных (глава 9), а не собственно к проблеме исследований процессов и объектов с помощью моделирования.

4.2. Алгоритмы

Решение задач на ЭВМ реализуется программным способом – путем выполнения последовательности операций, предусмотренных алгоритмом решения задачи. Алгоритм – это точная запись конечного числа действий, приводящих к решению задачи. Алгоритм определяет процесс преобразования информации от исходных данных к результатам. Рассмотрим пример простой задачи. Пусть поезд вышел из пункта A в момент времени t1 и прибыл в пункт B в момент tn. Во время следования поезда в моменты времени t1, t2, … ti, …, tn измерены значения скорости его движения v1, v2, … vi, …, vn. Требуется найти расстояние S от пункта A до пункта B.

Решение этой задачи, как и всякой другой, начато с построения модели явления (объекта). Как уже отмечалось, построение модели состоит в учете только существенных для рассматриваемых задач характеристик, описываемых ограниченным набором параметров. В нашем примере такими параметрами являются S, n и числовые массивы значений ti и vi , где i = 1, 2, …, n. Если мы хотим получить точное решение задачи, то требуется детальная модель, в рамках которой значения времени и скорости чаще регистрируются на тех участках пути, где скорость быстро изменяется.

Вторым этапом решения станет построение математической модели, в которой неизвестные параметры модели объекта (явления) связываются математическими выражениями с известными параметрами. В нашем простейшем примере только один параметр S не известен – построим математическую модель в виде равенства:

34

n 1

Sti 1 ti * vi vi 1 /2

i1

Символы * и / при описании алгоритмов означают умножение и деление. Следовательно, для вычисления расстояния от точки i до точки i+1 время движения на этом интервале умножается на среднюю скорость.

Третьим этапом будет построение алгоритма, отображающего точную последовательность операций при решении задачи с помощью компьютера. Изобразим этот алгоритм графически – в виде блок-схемы (Рис. 4.1).

В блоке 1 выполняются начальные присваивания: в начальный момент, когда поезд еще в точке A, i=1, а S=0. Операция присваивания очень важна для понимания компьютерной реализации алгоритмов. Дело в том, что при разработке программы для ЭВМ считается, что i и S – это не только обозначения математических переменных, но и обозначения ячеек памяти компьютера. Операция присваивания – это занесение нового значения в соответствующую ячейку. Присваивание отображает изменение значения соответствующей переменной в процессе реализации алгоритма. Чтобы отличать присваивание от обычного математического равенства, в некоторых языках программирования, например, в Паскале, операция присваивания обозначается не знаком равно (=), а двумя значками – двоеточием и равно (:=). В этом, вообще говоря, нет необходимости, т.к. знак равенства в математическом смысле при записи алгоритмов применяется только для проверки условий.

Рис. 4.1. Изображение алгоритма в виде блок-схемы

На блок-схемах проверка условий помещается в особые – логические блоки, обозначаемые не прямоугольником, а ромбом (см. блок 4 на рис. 4.1), а в программах инструкции по проверке условий начинаются со слова IF (если).

35

Вблоке 2 (см. рис. 4.1) пройденный путь получает приращение: в ячейку S помещается новое значение, равное прежнему, плюс значение пути за время от ti до ti+1. В блоке 3 наращивается значение i, т.к. мы собираемся повторить вычисления в блоке 2 для следующего интервала – при новом значении индекса i, увеличенном на 1. Но ведь последнее значение i, при котором надо вычислять приращение пути, равно n-1. Вот поэтому и проверяется условие ( i < n? ) в логическом блоке 4. До тех пор, пока это условие выполняется, повторно будут работать блоки 2, 3. Как только условие не выполнится, алгоритм завершит работу – к этому моменту в ячейке S накопится значение пройденного пути.

Врассмотренном алгоритме блоки 2-4 работают n-1 раз, т.е. выполняются циклически, и при каждом исполнении цикла переменные (содержимое ячеек) i и S обновляются. Именно циклы позволяют кратко записывать алгоритмы, в которых многие операции повторяются сотни, тысячи и даже миллионы раз.

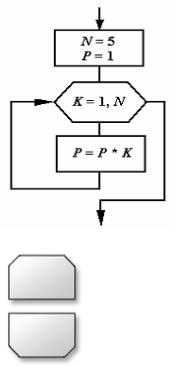
Валгоритмах выделяют три типа структур: последовательное выполнение, ветвление и повторение. Операции, выполняющиеся последовательно, образуют один блок, например, две операции присваивания в блоке 1. Блок либо получает управление более чем от одного блока (см. блок 2 на рис. 4.1), либо передаёт управление более чем одному блоку (см. блок 4), либо отделён от других блоков блоком одного из уже перечисленных типов (например, блок 3 на рис. 4.1). В последнее время для изображения циклов (структур повторения) на блок-схемах применяют специальные обозначения, позволяющие сделать блок-схемы компактнее. Так, изображение цикла, число повторений которого задано некоторой переменной N, иллюстрируется фрагментом блок-схемы на рис. 4.2, а для изображения циклов, завершающихся по условию, применяют символы, показанные на рис. 4.3.

Рис. 4.2. Фрагмент блок-схемы, изображающий цикл, работающий N раз; после выхода из цикла

P=120

Рис. 4.3. Символы, применяющиеся для изображения циклов, завершающихся по условию; условие записывается в одном из них; между этими символами размещаются блоки, выполняющиеся в цикле

36

В качестве примера алгоритма, в котором цикл завершается по условию, приведём блок-схему вычисления Y X (рис. 4.4).

Y=1

Рис. 4.4. Блок-схема вычисления квадратного корня

d = (X / Y – Y) / 2, Y = Y + d

Пока d > e

На этой блок-схеме показан итерационный алгоритм, т.е. значение квадратного корня вычисляется методом последовательных приближений. В качестве первого приближения взято Y=1. Если бы это предположение было верным, то оказалось бы, что d = 0. Здесь d – величина, на которую корректируется значение Y. Корректировки продолжаются до тех пор, пока d по абсолютной величине превышает некоторое очень маленькое число e, определяющее точность вычислений.

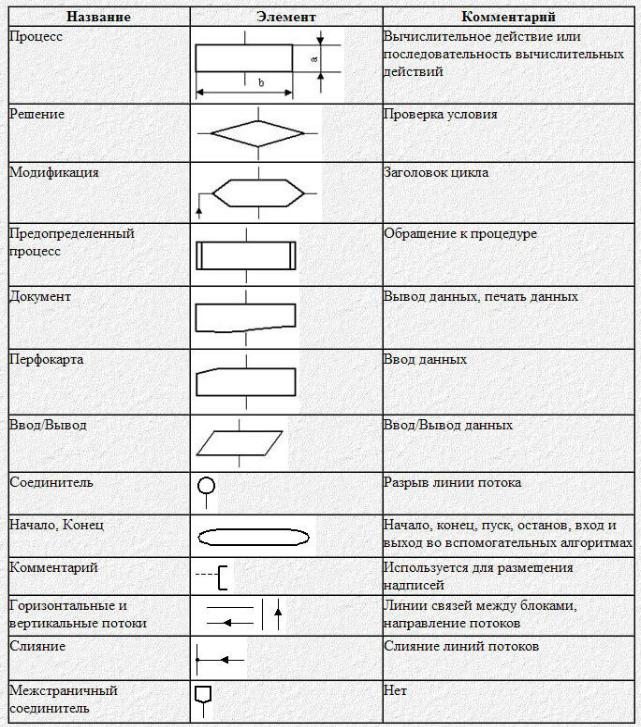
Таким образом, блок-схема – это последовательность блоков, предписывающих выполнение определенных операций, и связей между этими блоками. Внутри блоков указывается информация об операциях, подлежащих выполнению. В табл. 4.1 приведены наиболее часто используемые блоки, изображены элементы связей между ними и дано краткое пояснение к ним. Блоки и элементы связей называют элементами блок-схем.

Конфигурация и размеры блоков, а также порядок графического оформления блок-схем регламентированы ГОСТ 19002-80 и ГОСТ 19003-80 "Схемы алгоритмов и программ".

Алгоритм решения задачи имеет ряд обязательных свойств [4]:

дискретность – разбиение процесса обработки на более простые шаги,

определенность – однозначность выполнения каждого шага,

выполнимость – возможность получения результата за конечное число шагов,

массовость – пригодность алгоритма для решения некоторого класса задач.

Сцелью реализации на компьютере алгоритм записывают в виде программной процедуры (подпрограммы) на одном из языков программирования. Как уже отмечалось в разделе 2, современное приложение состоит из многих событийных и общих процедур. Для удобства записи текстов этих процедур

37

любая современная система программирования имеет в своем составе редактор текстов. Для получения работающего приложения система программирования компилирует процедуры, осуществляя переход от текстов на языке программирования к так называемым объектным модулям, которые состоят из машинных команд, но откомпилированные процедуры еще не увязаны друг с другом. Создание исполняемого приложения (EXE-файла) завершает редактор связей, также входящий в состав практически каждой системы программирования.

Таблица 4.1

Основные элементы, используемые в блок-схемах

38

4.3.Принципы структурного программирования

В70-е годы XX века объёмы и сложность программ достигли такого уровня, что «интуитивная» (неструктурированная) разработка программ, которая была нормой в более раннее время, перестала удовлетворять потребностям практики. Программы становились слишком сложными, чтобы их можно было нормально сопровождать, поэтому потребовалась систематизация процесса разработки и структуры программ. В результате в 70-х годах XX века была предложена Э. Дейкстроем, разработана и дополнена Н. Виртом методология создания программного обеспечения, получившая название структурного программирования.

Воснову этой методологии положены три принципа.

1.Любая программа представляет собой структуру, построенную из трёх типов базовых конструкций:

последовательное исполнение – однократное выполнение операций в том порядке, в котором они записаны в тексте программы;

ветвление – однократное выполнение одной из двух или более операций, в зависимости от выполнения некоторого заданного условия;

цикл – многократное исполнение одной и той же операции до тех пор, пока выполняется некоторое заданное условие (условие продолжения

цикла).

В программе базовые конструкции могут быть вложены друг в друга произвольным образом, но никаких других средств управления последовательностью выполнения операций не предусматривается.

2.Повторяющиеся фрагменты программы (либо не повторяющиеся, но представляющие собой логически целостные вычислительные блоки) могут оформляться в виде т. н. подпрограмм (процедур или функций). В этом случае в тексте основной программы, вместо помещённого в подпрограмму фрагмента, вставляется инструкция вызова подпрограммы. При выполнении такой инструкции выполняется вызванная подпрограмма, после чего исполнение программы продолжается с инструкции, следующей за командой вызова подпрограммы.

3.Разработка программы ведётся пошагово, методом «сверху вниз». Сначала пишется текст основной программы, в котором, вместо каждого

связного логического фрагмента текста, вставляется вызов подпрограммы, которая будет выполнять этот фрагмент. Вместо настоящих, работающих подпрограмм, в программу вставляются «заглушки», которые ничего не делают. Полученная программа проверяется и отлаживается. После того, как программист убедится, что подпрограммы вызываются в правильной последовательности (то есть общая структура программы верна), подпрограммы-заглушки последовательно заменяются на реально работающие, причём разработка каждой подпрограммы ведётся тем же методом, что и основной программы. Такая последовательность гарантирует, что на каждом этапе разработки программист одновременно имеет дело с обозримым и понятным ему множеством фрагментов, и

39

может быть уверен, что общая структура всех более высоких уровней программы верна.

При сопровождении и внесении изменений в программу выясняется, в какие именно процедуры нужно внести изменения, и они вносятся, не затрагивая части программы, непосредственно не связанные с ними. Это позволяет гарантировать, что при внесении изменений и исправлении ошибок не выйдет из строя какая-то часть программы, находящаяся в данный момент вне зоны внимания программиста.

Следование принципам структурного программирования сделало тексты программ, даже довольно крупных, нормально читаемыми. Серьёзно облегчилось понимание программ, появилась возможность разработки программ в нормальном промышленном режиме, когда программу может без особых затруднений понять не только её автор, но и другие программисты. Это позволило разрабатывать достаточно крупные программные комплексы силами коллективов разработчиков, и сопровождать эти комплексы в течение многих лет, даже в условиях неизбежных изменений в составе персонала.

Перечислим некоторые достоинства структурного программирования:

1.Структурное программирование позволяет значительно сократить число вариантов построения программы по одной и той же спецификации, что значительно снижает сложность программы и облегчает понимание её другими разработчиками.

2.В структурированных программах логически связанные инструкции находятся визуально ближе, а слабо связанные – дальше, что позволяет во многих случаях обходиться без блок-схем и других графических форм изображения алгоритмов.

3.Упрощается процесс тестирования и отладки структурированных программ.

4.4. Объектно-ориентированное программирование

Разработка алгоритмов и программ для вычислительных машин первых поколений выполнялась в соответствии с идеологией процедурного программирования, где данные и подпрограммы (процедуры, функции) их обработки формально не связаны. В настоящее время идеология процедурного программирования по-прежнему широко используется. Структурное программирование также направлено на совершенствование этой идеологии.

Принципиально другой идеологией алгоритмизации и программирования является ООП – объектно-ориентированное программирование. В настоящее время оно всё чаще используется для реализации очень больших и сложных проектов. Первым языком программирования, в котором были предложены принципы объектной ориентированности, была Симула. Она появилась в 1967 г., но тогда идеи ООП не были восприняты программистами: создававшиеся в те годы пакеты прикладных программ ещё не были столь масштабными, и их проще было разрабатывать средствами процедурного программирования. Затем концепции ООП были развиты Аланом Кэйем и Дэном Ингаллсом в

40