
- •8. Расчет плоских рам методом конечных элементов
- •8.1. Глобальная система координат. Вектор узловых перемещений и сил, матрица жесткости элемента в глобальной системе координат
- •8.2. Формирование матрицы жесткости и вектора узловых сил системы
- •8.3. Учет граничных условий
- •8.4. Алгоритм расчета стержневых систем на эвм
- •8.5. Пример расчета рамы на действие силовой нагрузки, температуры и смещение опор
8. РАСЧЕТ ПЛОСКИХ РАМ МЕТОДОМ КОНЕЧНЫХ ЭЛЕМЕНТОВ 72
8.1. Глобальная система координат. Вектор узловых перемещений и сил, матрица жесткости элемента в глобальной системе координат 72
8.2. Формирование матрицы жесткости и вектора узловых сил системы 74
8.3. Учет граничных условий 75
8.4. Алгоритм расчета стержневых систем на ЭВМ 76
8.5. Пример расчета рамы на действие силовой нагрузки, температуры и смещение опор 77
8. Расчет плоских рам методом конечных элементов
8.1. Глобальная система координат. Вектор узловых перемещений и сил, матрица жесткости элемента в глобальной системе координат
Стержневые конечные элементы могут соединяться в узлах под различными углами. В общем случае элементы системы работают как на растяжение-сжатие, так и на изгиб. Для суммирования всех сил, действующих на узел, необходимо эти силы представить в единой системе координат, которая называется глобальной (рис. 8.1).
|
Рис. 8.1. Стержневой элемент в локальной и глобальной системах координат |
Перемещения узлов системы также задаются в глобальной системе координат. В глобальной системе координат степени свободы удобно сгруппировать по узлам, а в локальной - по направлениям. Поскольку нумерация степеней свободы в локальной и глобальной системах координат различна, поэтому преобразования векторов перемещений и узловых сил из одной системы координат в другую можно записать в виде
|
(8.1) |
|
(8.2) |
где
|
(8.3) |
Матрица
![]() ортогональна и ее можно получить как
произведение двух ортогональных матриц
– булевой матрицы перестановок и матрицы
направляющих косинусов:
ортогональна и ее можно получить как
произведение двух ортогональных матриц
– булевой матрицы перестановок и матрицы
направляющих косинусов:
|
(75) |
Значения
ненулевых элементов матрицы
![]() даны в таблице 8.3.
даны в таблице 8.3.
Таблица 8.3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Локальная
нумерация
Глобальная
нумерация
оси
1
1
1
1
1
1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Матрица направляющих косинусов элемента состоит из двух одинаковых блоков для каждого узла:
|
(8.5) |
где
|
(8.6) |
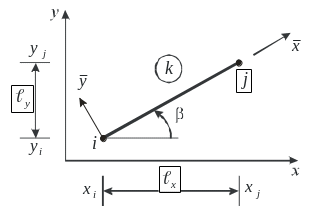
![]() – косинус угла
между осями
– косинус угла
между осями
![]() и
и
![]() ;
остальные элементы матрицы направляющих
косинусов имеют аналогичный смысл. В
[3] показано, что для вычисления синуса
и косинуса удобно воспользоваться
формулами
;
остальные элементы матрицы направляющих
косинусов имеют аналогичный смысл. В
[3] показано, что для вычисления синуса
и косинуса удобно воспользоваться
формулами
|
(8.7) |
Введем
обозначения
![]() ,
,
![]() и на основании (8.4) – (8.7) получим выражение
для матрицы преобразования элемента
(матрица поворота)
и на основании (8.4) – (8.7) получим выражение
для матрицы преобразования элемента
(матрица поворота)
|
(8.8) |
Матрица жесткости элемента в глобальной системе координат связывает глобальные узловые силы и перемещения:
|
(8.9) |
Матрица жесткости элемента в локальной системе координат состоит из двух блоков:
|
(8.10) |
матрица
![]() получена п.6.2 (формула 6.20), а
получена п.6.2 (формула 6.20), а
![]() определяется по формулам (7.23), (7.30), (7.32)
в зависимости от наличия шарниров в
узлах элемента. Если в обоих узлах
имеются шарниры, то
определяется по формулам (7.23), (7.30), (7.32)
в зависимости от наличия шарниров в
узлах элемента. Если в обоих узлах
имеются шарниры, то
![]() .
Аналогичную блочную структуру в локальной
системе координат имеет вектор узловых
сил от внеузловой нагрузки.
.
Аналогичную блочную структуру в локальной
системе координат имеет вектор узловых
сил от внеузловой нагрузки.


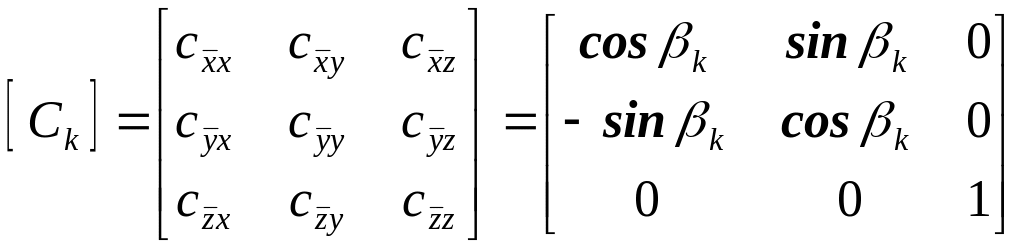 ;
;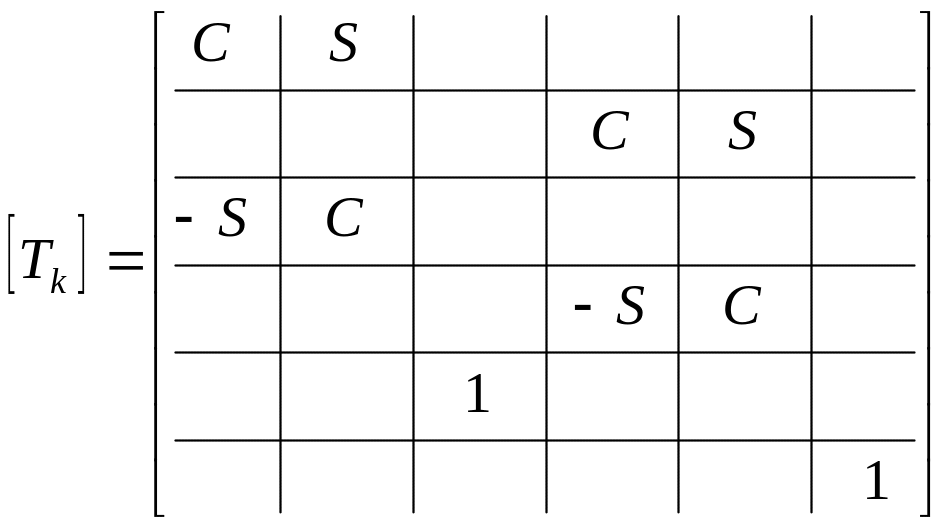
 ,
где
,
где