
TAU_OsipovaEA
.pdf
|
|
I1 x t dt, |
(1) |
0
где x t yуст y t - отклонение управляемой величины от нового установившегося значения, которое она будет иметь после завершения переходного процесса.
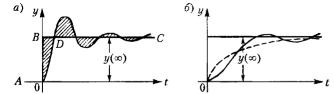
В устойчивой системе x 0 при t и этот интеграл имеет конечную величину. Геометрически это будет площадь под кривой переходного процесса, построенного для отклонения (рис. 1, а).
|
Площадь будет тем меньше, чем |
||
|
быстрее затухает переходный процесс и |
||
|
чем меньше величина отклонения. |
||
|
Поэтому |
параметры |
системы |
|
рекомендуется |
выбирать |
таким |
Рис. 1 |
образом, чтобы добиваться минимума |
||
этой интегральной оценки. |
|
||
|
|
||
Для вычисления интеграла (1) нет необходимости в нахождении x t , так как его
можно легко вычислить, используя изображение Лапласа или Хевисайда-Карсона. Действительно, изображение Лапласа определяется выражением
|
|
|
|
X p x t e pt dt. |
|
||
0 |
|
|
|
Отсюда следует, что интеграл (1) может быть найден посредством предельного |
|||
перехода p 0: |
|
|
|
|
|
|
|
x t dt lim |
x t e pt dt lim X p . |
||
0 |
p 0 |
0 |
p 0 |
|
|
||
Неудобством интегральной оценки вида (1) является то, что она годится только для монотонных переходных процессов, когда не меняется знак отклонения x . Если же имеет место колебательный процесс (рис. 1, б), то при вычислении интеграла (1) площади будут складываться алгебраически и минимум этого интеграла может соответствовать колебаниям с малым затуханием или вообще без затухания. Так как форма перереходного процесса при расчете систем управления может быть неизвестна, то применять интегральную оценку вида (1) оказывается практически нецелесообразным. Поэтому предлагается другая интегральная оценка (модульная):
I2 x t dt,
0
то есть сумма абсолютных величин всех площадей под кривой переходного процесса. Но оказалось, что вычисление ее по коэффициентам уравнения затруднительно.
В свете вышесказанного целесообразно перейти к квадратичной интегральной оценке
|
t dt, x 0 при t , |
|
I3 x2 |
(2) |
|
0 |
|
|
которая не зависит от знаков отклонений , а значит, и от формы переходного процесса(монотонной или колебательной).

|
Величина I3 (2) будет тем меньше, чем меньше сумма |
|
|
заштрихованных на рис. 2 площадей (взятых для квадратов |
|
|
ординат), то есть чем лучше переходный процесс |
|
|
приближается к идеальному скачку управляемой величины |
|
|
вслед за скачком задающего или возмущающего воздействия. |
|
Рис. 2 |
Заметим, что оценку (2) называют также квадратичной |
|
динамической ошибкой. |
||
|
||
|
Рассмотрим один из способов вычисления квадратично |
|
интегральной оценки (2). |
|
|
Изображение управляемой величины по Лапласу представляется в виде |
||
Y p |
|
b b p b pm 1 |
n m . |
|||||||||||||||||||||
|
|
0 |
|
1 |
|
|
m |
|
|
|
|
|
||||||||||||
|
a |
0 |
|
a p a |
n |
pn |
|
p |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда интегральная оценка может быть вычислена из выражения |
||||||||||||||||||||||||
I |
|
|
|
|
1 |
|
|
|
B |
|
B B |
|
2b b . |
|||||||||||
3 |
|
|
|
|
|
|
|
0 |
m |
|||||||||||||||
|
|
|
2a2 |
|
0 |
|
1 1 |
|
|
|
|
|
|
m |
|
0 1 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определитель находится следующим образом: |
||||||||||||||||||||||||
|
|
|
a0 |
|
|
|
a2 |
|
a4 |
a6 |
|
0 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
0 |
|
|
|
|
|
a1 |
a3 |
a5 |
|
|
|
0 |
|
|
|||||||
|
0 |
|
a0 |
|
a2 |
a4 |
|
0 |
|
. |
||||||||||||||
0 |
|
|
|
|
|
0 |
a |
a |
3 |
|
|
|
0 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
0 |
|
|
|
|
|
0 |
|
0 |
0 |
|
|
|
|
an 1 |
|
|
|||||
0,1, , m - определитель, получающийся из заменой 1 -го столбца столбцом
a1, a0 ,0, ,0.
Коэффициенты B1 , , Bm вычисляются следующим образом:
B0 b02 ,
B1 b12 2b0b2 ,
B b2 2b b 2 1 k b b ,
k k k 1 k 1 0 2k
Bm bm2 .
Недостатком интегральных оценок является то, что здесь ничем не ограничивается форма кривой переходного процесса. Оказывается, например, что три совершенно различных по форме процесса, изображенных на рис. 3, имеют одно и то же значение квадратичной интегральной оценки (2). Часто оказывается, что выбранные по минимуму этой оценки параметры системы соответствуют сильно колебательному
Рис.3
переходному процессу, ибо отмечавшееся уже при этом стремление приблизить процесс к идеальному скачку вызывает большую скорость процесса при подходе к установившемуся значению.
Это получается вследствие того, что оценка (2) учитывает только величину отклонения и быстроту затухания и никак не учитывает близость системы к колебательной границе устойчивости.
Если, например, подать на вход системы единичный скачок, то ошибка в переходном процессе определится заштрихованной частью на рис. 4, а. Очевидно, что величина интегральной оценки (2) будет тем меньше, чем ближе будет кривая переходного процесса к ломанной линии AOBC. Но приближение процесса к этой линии требует увеличения угла наклона кривой в начальной стадии процесса (приближение части кривой OD к отрезку OB).
Увеличение же начальной скорости может вызвать значительное перерегулирование и, следовательно, малый запас устойчивости.
Поэтому применяется еще другой вид интегральной оценки, в которой ограничение накладывается не только на величину отклонения x , но также и на скорость отклонения x . Эта улучшенная квадратичная интегральная оценка имеет вид
|
x2 T 2 x2 |
dt , |
|
Ik |
(3) |
||
0 |
|
|
|
где T - некоторая постоянная времени.
Рис. 4
Выясним, какой вид переходного процесса будет получаться при выборе параметров системы по минимуму улучшенной интегральной оценки (3). Для этого проделаем следующее преобразование:
|
|
|
|
0 |
|
|
Ik |
x Tx 2 dt |
2Txxdt |
x Tx 2 dt Tx2 |
Tx02 |
x Tx 2 dt, |
|
0 |
0 |
0 |
|
x0 |
0 |
|
|
|
|||||
|
|
|
где x0 - начальное значение отклонения в переходном процессе.
Наименьшее значение последнего выражения будет при выполнении условия
Tx x Tp 1 x 0.
Это дифференциальное уравнение первого порядка, решение которого имеет вид
|
|
t |
|
|
|
|
|
t |
|
|
x x e |
|
y y |
e |
|
|
|||||
T , |
1 |
T , |
(4) |
|||||||
0 |
|
|
|
|
уст |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где x0 yуст - установившее значение управляемой величины.
Этот процесс изображен на рис. 4 пунктиром. Следовательно, выбирая параметры системы по минимуму улучшенной интегральной оценки (3), можно приблизить переходный процесс к заданной экспоненте (4) с постоянной времени T , которая носит в этом случае название экстремали.
Выбор параметров системы по улучшенной интегральной оценки приводит к менее колебательным процессам по сравнению с использованием обычной квадратичной интегральной оценки (2).
В принципе возможно использование более сложных выражений, чем (3), в которые кроме первой производной от отклонения будут входить вторая, третья и т.д. производные. Экстремаль в данном случае будет соответствовать более сложной кривой, чем экспонента, что позволяет точнее задать желаемый вид переходного процесса.
Тема 3.7. Инвариантные системы. Комбинированное управление
Проблема инвариантности - это проблема определения таких структур и параметров системы управления, при которых влияние некоторых произвольно изменяющихся внешних возмущений и собственных параметров системы на динамические характеристики процессов управления могут быть частично или полностью скомпенсированы.
Задача инвариантности возникает и в более простой постановке, когда требуется сделать по возможности независимой ту или иную переменную (обобщенную координату) от одного или нескольких внешних воздействий. Такими воздействиями могут быть возмущающие силы, нагрузка или помехи, но это могут быть и некоторые полезные (управляющие) воздействия, которые должны вызывать изменения одних переменных и не должны оказывать влияние на некоторые другие координаты системы.
Если внешнее воздействие допускает прямое или косвенное измерение, то точность системы может быть повышена за счет комбинированного управления. под комбинированным управлением понимается такой метод построения автоматических систем, когда наряду с замкнутым контуром регулирования по отклонению используется регулирование по задающему или возмущающему воздействию. Таким образом, комбинированное управление сочетает принципы регулирования по замкнутому и разомкнутому циклам.
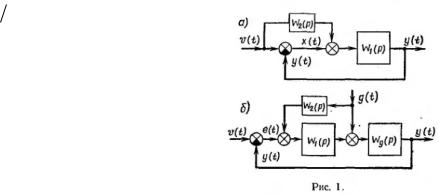
Рассмотрим случай комбинированного управления по задающему воздействию. структурная схема системы управления изображена на рис. 1, а.
Если |
осуществлять |
регулирование |
только по отклонению, то есть положить |
W2 p 0 , то |
1 W1 p , |
|
|
Y p W1 p V p |
(1) |
||
где W1 p |
- передаточная функция |
разомкнутой |
|
системы. |
|
|
|
|
|
|
При введении |
регулирования по |
|||||
воздействию получим |
|
|
|
|||
Y p |
|
W1 p |
|
|
1 W2 p V p . |
|
1 |
W1 p |
|||||
|
|
|||||
задающему
(2)
Из последнего уравнения видно, что введение регулирования по задающему воздействию не меняет
характеристического уравнения системы, работающей по отклонению, так как знаменатели в уравнениях (1) и (2) одинаковые. Это означает, что при комбинированном управлении сохраняются не только условия устойчивости, но и оценки качества переходного процесса, основанные на использовании корней характеристического уравнения.
Передаточная функция по ошибке
х p |
1 W2 p W1 |
p |
. |
|||
1 W1 |
p |
|
||||
|
|
|||||
Положив |
|
|
|
|
|
|
W2 p 1 W1 p , |
|
|
|
(3) |
||
получим х p 0 , т.е. ошибка системы не будет зависеть от задающего воздействия.
Условие (3) называется условием полной инвариантности (то есть независимости) системы по отношению к задающему воздействию. Поскольку реальные системы представляют собой различные комбинации инерционных и интегрирующих звеньев, то
(3) можно представить в виде
W p a |
0 |
a p a |
2 |
p2 |
a |
3 |
p3 |
. |
(4) |
||
2 |
|
1 |
|
|
|
|
|
|
|||
Для |
астатических |
систем |
a0 0 . Из (4) видно, что при |
комбинированном |
|||||||
управлении для получения полной инвариантности необходимо вводить первую и высшие производные от задающего воздействия. На практике получение высших производных (выше второй) затруднительно, поэтому может быть получена не полная, а частичная инвариантность с точностью до некоторой величины .
Комбинированное управление может быть использовано также для уменьшения влияния контролируемого возмущающего воздействия g t , приложенного в какой-либо точке системы (рис. 1, б). При этом передаточная функция по возмущению
Wyg p Wg p W2 p Wp p  1 Wp p ,
1 Wp p ,
где Wp p W1 p Wg p - передаточная функция разомкнутой системы; Wg p - передаточная функция по данному возмущению в разомкнутой системе.
Полная инвариантность может быть получен при Wyg p 0 , т.е.
W2 p Wg p 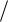 Wp p .
Wp p .
Если есть возможность контролировать несколько возмущений в разных точках системы, то можно рассчитать условия инвариантности по каждому из них.
Тема 3.8. Управляемость и наблюдаемость систем управления Раздел 4. Синтез систем управления
Тема 4.1. Оптимальные системы
Под оптимальной системой автоматического управления понимают систему, в которой управление осуществляется таким образом, что некоторый показатель качества ее работы, принимаемый за критерий оптимальности, имеет экстремальное (чаще всего минимальное) значение. В качестве критерия оптимальности могут быть выбраны время переходного процесса, энергетические показатель работы системы, интегральные оценки качества переходных процессов и др.
В теории оптимальных систем существует два направления: оптимальное управление в детерминированных системах и оптимальное управление в стохастических системах.
Обратимся к рассмотрению первого направления. Основой теории является классическое вариационное исчисление, принцип максимума Л.С. Понтрягина и динамическое программирование Р. Беллмана. Большой вклад в теорию оптимальных систем внесли советские ученые А.М. Летов, Н.Н. Красовский, А.А. Красовский, А.А. Фельдбаум и другие.

Приведем классический пример задачи управления, в основе решения которой лежит математический приём известный как принцип максимума.
Задача состоит в определении оптимальной траектории движения ракеты. Управляющие параметры в такой задаче – это моменты включения двигателей и длительность их работы, величина и направление силы тяги, которую следует приложить к ракете в каждый отдельный момент времени. Режим работы двигателей выбирается в зависимости от ряда ограничений, например, в зависимости от общего количества ракетного топлива, имеющегося на борту. Фазовыми переменными, описывающими траекторию ракеты, являются её масса, а также положение и скорость относительно фиксированной системы координат. Зависимость фазовых координат от силы тяги выражается с помощью системы дифференциальных уравнений, получаемых на основе законов физики. В результате расчет траектории предстоящего космического полета заключается в отыскании максимума некоторого целевого функционала.
Постановка задачи
Авторы принципа максимума, Лев Семенович Понтрягин со своими учениками, в свое время рассмотрели ряд задач математического и прикладного характера, в которых управляемые процессы могут быть описаны системой обыкновенных дифференциальных уравнений
|
dxi |
f i (x1, ..., xn ,u1, ..., ur ), |
i 1, ..., n. |
(1) |
|
||
|
|
|
|||||
|
dt |
|
|
|
|
|
|
Здесь |
x1, ... , xn |
− величины, характеризующие |
процесс, т.е. |
фазовые |
|||
координаты |
управляемого |
объекта, |
определяющие его состояние в каждый |
момент |
|||
времени t ; u1, ..., ur − параметры управления, определяющие ход процесса, и t − время. Заметим, что система (1) автономна, то есть правые её части не зависят явно от времени t .
Эта же система дифференциальных уравнений в векторной форме:
dx f (x, u). dt
Для того чтобы ход управляемого процесса (1) был определён на некотором отрезке времени t0 t t1 , достаточно, чтобы на этом отрезке времени были заданы (как
функции времени) параметры управления u1, ..., ur :
u j u j (t), |
j 1, ... , r. |
(2) |
||
Тогда при заданных начальных значениях |
|
|||
xi (t |
0 |
) xi , |
i 1, ... , n, |
(3) |
|
0 |
|
|
|
решение системы (1) определяется однозначно. Подлежащая решению вариационная задача, связанная с управляемым процессом (1), заключается в следующем. Рассматривается интегральный функционал
|
t1 |
|
|
J f 0 (x1 , ... , xn , u1, ... , ur )dt, |
(4) |
|
t0 |
|
где |
f 0 (x1, ..., xn , u1, ..., ur ) - заданная |
функция. Для каждого управления (2), |
заданного на некотором отрезке t0 t t1 , однозначно определяется ход управляемого процесса, и интеграл (4) принимает определенное значение. Допустим, что существуют

управления (2), переводящие управляемый объект из заданного фазового состояния (3) в предписанное конечное фазовое состояние
xi (t ) xi , i 1, ..., n . |
(5) |
|
1 |
1 |
|
Требуется отыскать управление |
|
|
u j (t), j 1, ... , r, |
(6) |
|
которое осуществляет переход управляемого объекта из состояния (3) в состояние (5) таким образом, чтобы функционал (4) имел минимальное значение. При этом моменты
времени t0 и t1 в рассматриваемой постановке задачи не фиксируются, а требуется
только, чтобы в начальный момент времени объект находился в состоянии (3), а в конечный момент – в состоянии (5) и чтобы функционал (4) достигал минимума. В
частном случае, когда функция f 0 (x1, ..., xn , u1, ..., ur ) , определяющая функционал (4),
тождественно равна единице, функционал (4) имеет величину t1 t0 , и наша вариационная задача превращается в оптимальную задачу быстродействия.
В технических задачах, где параметры управления u1 ,...,ur определяют, например, положение рулей машины, эти параметры не могут принимать произвольных
значений, а подчинены некоторым ограничениям. Скажем, u1 может принимать лишь значения, удовлетворяющие условию
u1 1.
Причем это условие означает, что для руля допустимы и его крайние положения,
когда u1 1, |
могущие, в частности, давать оптимальное управление. Для |
объекта |
|||||||
снабженного r |
«рулями», от положения которых зависит движения объекта, положения |
||||||||
«рулей» характеризуются точками |
u (u1, u2 ,...,ur ) U |
некоторой |
области |
||||||
управления |
U , |
которая |
может быть |
любым множеством |
некоторого r - |
мерного |
|||
евклидова пространства |
Er . Физический |
смысл замкнутой |
и |
ограниченной |
области |
||||
управления |
U |
ясен: |
управляющими |
параметрами u1,u2 ,...,ur |
могут |
служить |
|||
количество подаваемого в двигатель топлива, температура, сила тока, напряжение и т. п., которые не могут принимать сколь угодно больших значений. Кроме того, между
управляющими параметрами могут существовать связи, что делает область U геометрически более или менее сложной.
Предполагается обычно, что |
класс допустимых управлений u j (t), j 1, ... , r |
состоит из кусочно-непрерывных |
функций, заданных на отрезке t0 t t1 , и |
принимающих значения из области |
управления U . Кусочно-непрерывные функции |
непрерывны для всех рассматриваемых t , за исключением лишь конечного числа моментов времени, где функция может терпеть разрывы первого рода. Кусочнонепрерывные управления соответствую предположению о «безынерционности» рулей, так
как значения функций u j (t), j 1, ... , r могут (в моменты разрыва) мгновенно перескакивать с одной точки области управления в другую.
Фазовые координаты x1, ..., xn считаются непрерывными и кусочнодифференцируемыми функциями времени.
Принцип максимума

Переходим теперь к формулировке принципа максимума, дающего решение поставленной основной задаче. Для этого будет удобно к фазовым координатам
x1, ..., xn , меняющимся по закону (1)
|
|
dxi |
f i (x1 , ... , xn ,u1 , ... , u r ), |
i 1, ... , n; |
|
||
|
|
|
|
|
|||
|
|
dt |
|
|
|
||
добавить ещё одну координату x 0 , закон изменения которой имеет вид |
|
||||||
|
dx0 |
f 0 |
(x1, x2 ,..., xn ,u1,u2 ,...,ur ), |
(7) |
|||
|
|
||||||
|
dt |
|
|
|
|||
где f 0 - функция, участвующая в определении функционала J . |
|
||||||
Функции |
f i , i 0,1, ..., n предполагаются непрерывными по |
совокупности |
|||||
переменных x1, ..., xn и непрерывно дифференцируемыми по x1, ..., xn , поэтому можно построить ещё одну систему уравнений относительно вспомогательных переменных
0 , 1, ..., n :
|
d |
i |
|
n |
f (x,u) |
|
|||
|
|
|
|
|
|
, i 0,1, ..., n. |
(8) |
||
|
dt |
|
|
x |
i |
||||
|
|
|
0 |
|
|
|
|
||
Системы |
(7) |
и (8) |
можно объединить с помощью функции |
Гамильтона |
|||||
переменных x1, ..., xn , 0 , 1, ..., n , u1,u2 ,...,ur :
n
H f (x, u) .
0
Непосредственно проверяется, что системы (7) и (8) могут быть с помощью этой функции записаны в виде следующей гамильтоновой системы:
dxi |
H |
|
|
|
|
|
, i 0,1, ..., n, |
|
i |
||
dt |
|
||
d i H , i 0,1, ..., n. dt xi
Теорема 1. Для оптимальности управления u(t)
существование такой ненулевой вектор-функции соответсвующей функциям u(t) и x(t) , что:
(9)
(10)
и траектории x(t) необходимо
ψ(t) ( 0 (t), 1(t),... , n (t)) ,
1. |
при любом |
t , t0 t t1 , функция |
|
переменного u U достигает в |
точке u u(t) максимума. |
|
|
||
2. |
в любой момент времени t , t0 t t1 , выполнены соотношения |
|||
0 |
(t) 0, |
max H ψ(t), x(t) 0. |
|
|
|
|
u U |
|
|
Теорема 2. Пусть u t , |
t0 t t1 |
- |
допустимое управление, переводящее |
||||||||||||||||||
фазовую точку из положения x0 |
в положение x1 , а x t - соответствующая траектория, |
||||||||||||||||||||
так что x t0 x0 , x t1 x1 . Для |
оптимальности (по быстродействию) управление u t и |
||||||||||||||||||||
траектории |
x t |
|
необходимо |
существование |
такой |
ненулевой |
вектор-функции |
||||||||||||||
ψ(t) ( 1 (t),..., n (t)) , соответствующей функциям u t и x t , что: |
|
|
|||||||||||||||||||
1. |
для всех |
t , t0 t t1 , функция |
|
переменного u U достигает в точке |
|||||||||||||||||
u u(t) максимума. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2. |
в любой момент времени t , t0 t t1 , выполнены соотношения |
|
|||||||||||||||||||
|
max H ψ(t), x(t) 0. |
|
|
|
|
|
|
|
|
|
|||||||||||
|
u U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рассмотрим |
уравнение |
|
d 2 x |
u , где |
u вещественный |
управляющий |
параметр, |
||||||||||||||
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dt2 |
|
|
|
|
|
|
|
||
подчиненный |
условию |
|
u |
|
1. |
|
В |
фазовых координатах |
x1 x, |
x2 |
dx |
это |
уравнение |
||||||||
|
|
|
|||||||||||||||||||
|
|
|
dt |
||||||||||||||||||
переписывается в виде следующей системы: |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
dx1 |
x2 , |
dx2 |
|
u. |
|
|
|
|
|
|
|
|
|
(11) |
|
|||||
|
dt |
dt |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рассмотрим (для фазовой точки, движущейся по закону (11)) задачу о быстрейшем |
|||||||||||||||||||||
попадании в начало координат |
0,0 из заданного начального состояния x0 . Иначе говоря, |
||||||||||||||||||||
мы будем рассматривать задачу об оптимальном быстродействии в случае, когда |
|||||||||
конечным положением служит начало координат: x1 |
0,0 . |
||||||||
Функция H в рассматриваемом случае имеет вид |
|||||||||
H |
x2 u. |
|
|
|
(12) |
||||
1 |
|
2 |
|
|
|
|
|
||
Далее, для вспомогательных переменных 1, 2 |
мы получаем систему уравнений |
||||||||
|
d 1 |
0, |
d 2 |
|
|
, |
|
||
|
|
|
1 |
|
|||||
|
dt |
|
dt |
|
|
|
|||
|
|
c1,c2 постоянные . Условие 1 теоремы 1 дает нам (учитывая |
|||||||
откуда 1 с1, 2 |
с2 с1t |
||||||||
(12) и условие 1 u 1 ) |
|
|
|
|
|||||
u t sign 2 t sign c2 c1t . |
(13) |
||||||||
Из (13) следует, что каждое оптимальное управление u t , t0 t t1 , является |
|||||||||
кусочно-постоянной функцией, принимающей значения 1 и имеющей не более двух |
|||||||||
интервалов постоянства (ибо линейная функция c2 c1t не более одного раза меняет знак на отрезке t0 t t1 ). Обратно, любая такая функция u t может быть получена из соотношения (13) при некоторых значениях постоянных с1,с2 .
Для отрезка времени, на котором u 1, мы имеем (в силу системы (11))
|
|
|
2 |
|
|
|
|
|
s |
2 |
2 |
|
x2 t s2 , |
x1 |
t |
|
s2t s1 |
1 |
t s2 2 |
s1 |
|
|
|
, |
|
|
|
|
|
|
|
|||||||
|
2 |
|
2 |
|
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
( s1, s2 постоянные интегрирования), откуда получаем

x1 |
1 |
x2 2 |
s, |
(14) |
|
2 |
|||||
|
|
|
|
где s s1 12 s2 2 - постоянная. Таким образом, кусок фазовой траектории, для которого
u 1, представляет собой дугу параболы (14). Семейство парабол (14) показано на рис. 1,
а.
Аналогично, для отрезка времени, на котором u 1, мы имеем x2 t s 2 ,
|
|
2 |
|
|
|
|
|
s |
2 |
2 |
|
x1 |
t |
|
s 2t s 1 |
1 |
t s 2 2 |
s 1 |
|
|
|
, |
|
|
|
|
|
|
|
||||||
2 |
|
2 |
|
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
откуда получаем |
|
|
|
|
|
|
|
|
|||
|
x1 |
1 |
x2 2 s . |
|
|
|
(15) |
|
|||
|
|
|
|
|
|
||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
Семейство парабол (15) показано на рис. 1, б. По параболам (14) фазовые точки |
||||||||||
движутся снизу вверх (ибо |
|
dx2 |
|
u 1), а по параболам (15) - сверху вниз ( |
dx2 |
|
u 1). |
||||
|
dt |
dt |
|||||||||
|
|
|
|
|
|
|
|
||||
u t |
Как было указано выше, каждое оптимальное управление |
|
|||||||||
является кусочно-постоянной функцией, принимающей |
|
||||||||||
значения 1 и имеющей не более двух интервалов постоянства. |
|
||||||||||
Если управление u t сначала, в течение некоторого времени, |
|
||||||||||
равно |
1 , а затем равно |
1, то фазовая траектория состоит из |
|
||||||||
двух |
кусков парабол (рис. 2, |
а), примыкающих друг к другу, |
|
||||||||
причем второй |
из этих кусков лежит на той из парабол (15), |
|
|||||||||
которая проходит через начало координат (ибо искомая |
|
||||||||||
траектория должна вести в начало координат). Если же, наоборот, |
|
||||||||||
сначала u 1, |
а затем |
u 1, то фазовая кривая заменяется |
|
||||||||
центрально симметричной (рис. 2, б). |
Рис. 1 |
|
|
На рис.2 подписаны на дугах парабол |
|
соответствующие значения управляющего |
|
параметра u . На рис. 3 изображено все |
|
семейство полученных таким образом фазовых |
|
траекторий (АО - дуга параболы x1 1 x2 2 , |
|
2 |
|
расположенная в нижней полуплоскости; ВО - |
|
дуга параболы x1 1 x2 2 , расположенная в |
|
2 |
Рис. 3 |
верхней полуплоскости). Фазовая точка |
|
движется по проходящей через начальную точку |
x0 дуге параболы (15), если точка x0 |
расположена выше линии АОВ, и по дуге параболы (14), если точка x0 расположена ниже этой линии. Иначе говоря, если начальное положение x0 расположено выше линии АОВ,
то фазовая точка должна двигаться под воздействием управления u 1 до тех пор, пока она не попадет на дугу АО; в момент попадания на дугу АО значение u переключается и становиться равным 1 вплоть до момента попадания в начало координат. если же начальное положение x0 расположено ниже линии АОВ, то u должно быть равно 1 до
