TAU_OsipovaEA
.pdf
называется колебательной. В системе в этом случае устанавливаются незатухающие гармонические колебания с амплитудой Ak и частотой k .
При наличии двух (кратных) нулевых корней pk pk 1 0 соответствующая им сумма составляющих решения (2), как известно, представляется в виде
Ck Ck 1t e pk t Ck Ck 1t ,
т.е. при Ck 1 0 она неограниченно увеличивается. Поэтому в данном случае систему
следует рассматривать как неустойчивую.
3. Если есть хоть один корень в правой полуплоскости комплексной плоскости, то система неустойчива.
Тема 3.4. Алгебраические критерии устойчивости. Критерии Гурвица и Рауса
Критерий Гурвица
Пусть дано характеристическое уравнение системы
a |
n |
pn a |
n 1 |
pn 1 ... a p a |
0 |
0. |
(1) |
|
|
1 |
|
|
Необходимо составить определитель Гурвица, содержащий n строк и n столбцов, из коэффициентов уравнения
|
an 1 |
an 3 |
an 5 |
0 |
|||
|
an |
an 2 |
an 4 |
0 |
|||
|
0 |
an 1 |
an 3 |
0 |
|||
n |
0 |
an |
an 2 |
0 |
|||
0 |
0 |
an 1 |
|
0 |
|||
|
|||||||
|
|
|
|
|
|
||
|
0 |
0 |
0 |
a3 |
a1 |
0 |
|
|
0 |
0 |
0 |
a4 |
a2 |
a0 |
|
Далее составляются главные диагональные миноры определителя Гурвица:
|
|
a |
|
|
|
|
|
|
an 1 |
an 3 |
|
|
|
|
an 1 |
an 3 |
an 5 |
|||
|
|
|
|
|
|
|
||||||||||||||
1 |
n 1 |
; |
2 |
|
; |
3 |
a |
n |
a |
n 2 |
a |
n 4 |
||||||||
|
|
|
|
|
|
an |
an 2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
an 1 |
an 3 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
и т.д. до n включительно.
Критерий устойчивости Гурвица формулируется следующим образом. Для устойчивости линейной системы автоматического регулирования с характеристическим
уравнением (1) необходимо и достаточно, чтобы при an 0 все главные диагональные миноры определителя Гурвица были положительны. Если выполнены все условия критерия Гурвица, кроме одного n 1 0 , то характеристическое уравнение системы имеет пару сопряженных чисто мнимых корней и система находится на границе колебательной устойчивости. Если же выполнены все условия Гурвица, кроме a0 0 , то
уравнение имеет один нулевой корень (это следует из непосредственного рассмотрения характеристического уравнения (1)) и система находится на границе апериодической устойчивости.
Критерий Рауса
Пусть дано характеристическое уравнение системы (1).
Составим таблицу Рауса.
Число строк таблицы Рауса равно степени уравнения плюс единица, т.е. n 1 . Коэффициентам с отрицательными индексами соответствуют нули.
Критерий устойчивости Рауса формулируется следующим образом. Для устойчивости системы автоматического регулирования необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса были положительны, т.е. чтобы
c11 0;c12 0;c13 0;c14 0; ;c1,n 1 0.
При составлении таблицы Рауса для численно заданных коэффициентов уравнения в целях упрощения вычислений можно умножать или делить строки таблицы на положительную величину. Это не меняет результат.
Если не все коэффициенты первого столбца положительны, т.е. система неустойчива, то число корней уравнения, лежащих в правой полуплоскости, равно числу перемен знаков в первом столбце таблицы.
Нуль в предпоследней строке первого столбца таблицы Рауса свидетельствует о появлении пары чисто мнимых сопряженных корней характеристического уравнения (граница колебательной устойчивости). При этом последняя строка таблицы не
рассчитывается, поскольку для нее rn 1 . При a0 0 в нуль обращается c1,n 1, что
соответствует появлению одного нулевого корня характеристического уравнения (граница апериодической устойчивости).
Тема 3.5. Частотные критерии устойчивости. Критерии Михайлова и Найквиста
Критерий Михайлова
В основе критерия Михайлова лежит известный в теории функций комплексного переменного принцип аргумента. Согласно этому принципу приращение аргумента функции f комплексного переменного p при изменении его по замкнутому контуру в
положительном направлении (против часовой стрелки) составляет |
2 N p , где N - |
||
число нулей, а |
p - число |
полюсов функции f p внутри |
замкнутого контура. |
Предполагается, |
что функции |
f p аналитична внутри этого контура(кроме конечного |
|
числа полюсов) и не имеет нулей и полюсов на контуре. Если применить принцип аргумента к полиному
D p an pn an 1 pn 1 ... a1 p a0 ,
стоящему в левой части характеристического уравнения, используя в качестве контура мнимую ось p j , замкнутую полуокружность бесконечного радиуса, то можно получить критерий Михайлова. Приведем его доказательство.
Пусть дано характеристическое уравнение
D p an pn an 1 pn 1 ... a1 p a0 0.
Полином D p можно представить в виде
D p an p p1 p p2 p pn ,
где pi - корни характеристического уравнения.
Положим p j , тогда
D j an j p1 j p2 j pn .
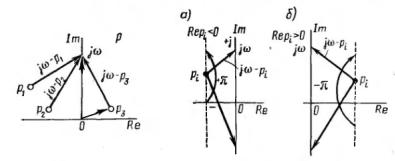
Рассмотрим геометрическое представление комплексных чисел j pi на комплексной плоскости p . Начала векторов, изображающих комплексные числа, лежат в точках pi , а концы – на мнимой оси в точке j (рис.1).
Рис. 1 Рис. 2 Найдем аргумент комплексного числа D j :
|
n |
|
|
arg D j arg j pi . |
|
||
|
i 1 |
|
|
Изменение аргумента D j с изменением от до равно |
|||
|
n |
|
|
arg D j arg j pi . |
(1) |
||
|
i 1 |
|
|
Согласно (1) для определения изменения аргумента необходимо подчитать сумму |
|||
изменений аргументов двучленов j pi . |
Изменения аргументов зависят от того, в |
||
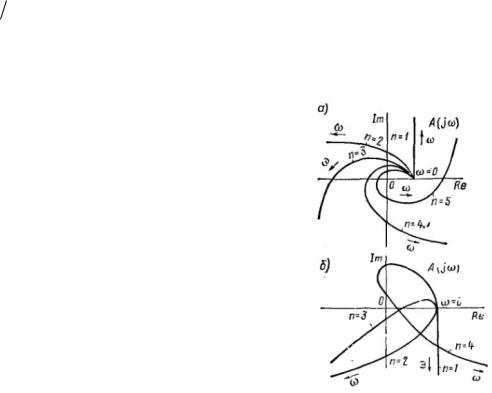
какой (правой или левой) полуплоскости лежат корни pi . Рассмотрим два случая. Пусть корень pi лежит в левой полуплоскости (рис. 2, а). При изменении от до конец вектора j pi скользит вдоль мнимой оси снизу вверх, поворачиваясь против часовой стрелки на 180 , при этом изменение аргумента
arg j pi . |
(2) |
|
|
Если корень pi лежит в правой полуплоскости (рис. 2, |
б), то, рассуждая |
аналогично, получим
arg j pi . |
(3) |
|
|
Допустим, что уравнение D p 0 имеем l |
корней в правой полуплоскости и |
n l корней в левой полуплоскости (порядок уравнения равен |
n ). Тогда на основании |
(1), (2), (3) |
|
arg D j n 2l . |
(4) |
|
|
Выражение (4) и представляет собой запись принципа аргумента для характеристического полинома D p .
Для устойчивости системы автоматического регулирования, имеющей характеристическое уравнение необходимо и достаточно, чтобы число правых корней l было равно нулю, при этом
arg D j n. |
(5) |
|
D j будет монотонно возрастать с |
Заметим, что при l 0 аргумент |
|
увеличением . |
|
Критерий Михайлова является наглядной графической интерпретацией формулы
(5). При построении годографа характеристического вектора D j , называемого годографом Михайлова, можно ограничиться половинным диапазоном изменения0 , так как для полиноминальной функции от j справедливы равенства
Re D j Re D j ;
Im D j Im D j ,
и часть годографа D j , соответствующая отрицательным значениям , представляет собой зеркальное отражение относительно действительной оси части годографа D j
для положительных . При изменении в половинном диапазоне
arg D j n 2.
0
Согласно критерию Михайлова для устойчивости системы автоматического регулирования необходимо и достаточно, чтобы годограф характеристического вектора
D j , начинаясь при 0 на действительной оси, с
ростом от 0 до обходил последовательно в положительном направлении (против часовой стрелки) n квадрантов, где n - порядок характеристического уравнения.
На рис.3, а показаны годографы Михайлова для устойчивых систем при различных значениях n . Все ни начинаются при 0 со значения a0 на положительной
действительной полуоси. Это означает, что характеристические уравнения приведены к виду, при котором их коэффициенты положительны. Годографы, изображенные на рис. 3, а, уходят в бесконечность прии обходят соответствующее число квадрантов в положительном направлении.
Рис.3
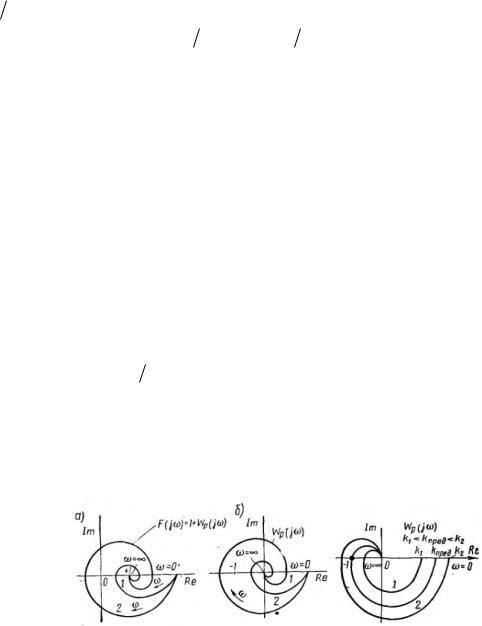
На рис. 3, б показаны годографы неустойчивых систем. Все они не удовлетворяют
условию обхода n квадрантов в положительном направлении. |
|
||
Критерий Найквиста |
|
|
|
Пусть |
передаточная функция разомкнутой |
системы |
регулирования |
Wp p K p |
D p . Образуем функцию |
|
|
F p 1 Wp p D p K p D p A p |
D p . |
(6) |
|
Числитель этой функции представляет собой характеристический полином
замкнутой системы, знаменатель – характеристический полином разомкнутой системы. |
||||
Пусть степень D p |
равна n , а степень |
K p |
равна |
m n . Степень |
характеристического полинома замкнутой системы K p D p также равна n .
Рассмотрим три случая состояния разомкнутой системы: устойчива, неустойчива и находится на границе устойчивости, причем в последнем случае характеристическое
уравнение разомкнутой системы D p 0 имеет нулевой корень кратности , то есть
D p p D1 p .
I случай – система в разомкнутом состоянии устойчива.
Согласно критерию устойчивости Михайлова изменение аргумента характеристического полинома разомкнутой системы
arg D j n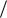 
2.
0
Если потребовать, чтобы система в замкнутом состоянии была устойчива, то
должно удовлетворяться равенство |
|
|
|
arg D j K j n 2. |
|
|
|
0 |
|
|
|
При этом из (6) следует, что |
|
|
|
arg F j arg D j K j arg D j 0. |
(7) |
||
0 |
0 |
0 |
|
Таким образом, система автоматического регулирования устойчива, если (и только |
|||
если) изменение аргумента вектора F j при изменении от |
0 до равно нулю. |
||
|
Рис. 4 |
|
На рис. 4, а показаны два |
годографа F j 1 Wp j : |
1 соответствует |
устойчивой системе, так как он не охватывает точку 0, j0 ; 2 – неустойчивой, так как он |
||
охватывает точку 0, j0 . Поскольку |
F j отличается от Wp j на |
1, то условие |
устойчивости можно получить непосредственно для характеристики Wp j (рис. 4, б).
Приведем формулировку критерия Найквиста для этого случая. Для устойчивости замкнутой системы автоматического регулирования необходимо и достаточно, чтобы
частотный годограф разомкнутой системы Wp j при изменении от 0 до не
охватывал точку 1, j0 .
II случай – система в разомкнутом состоянии неустойчива.
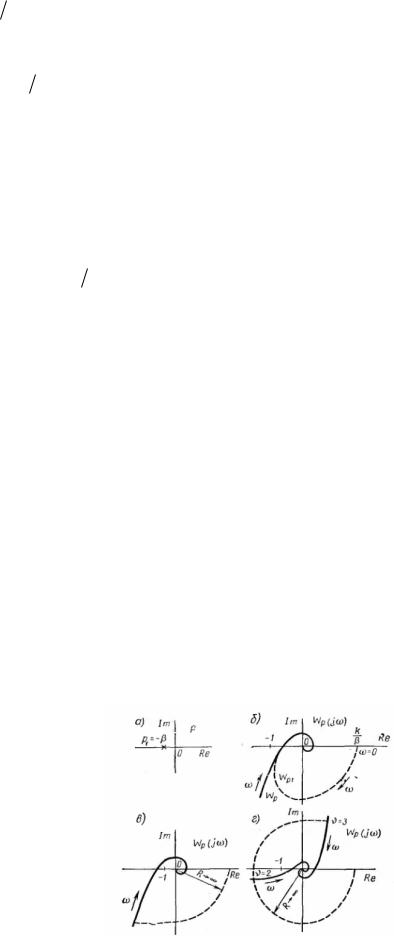
Пусть система в разомкнутом состоянии неустойчива, при этом характеристическое уравнение разомкнутой системы имеет l корней в правой
полуплоскости. тогда согласно принципу аргумента (4), учитывая симметрии характеристик для и , получим
arg D j n 2l 2. |
|
||
|
0 |
|
|
если потребовать, чтобы система в замкнутом состоянии была устойчивой, то |
|||
должно выполняться равенство |
|
|
|
arg D j K j n 2. |
|
||
|
0 |
|
|
При этом с учетом (7) |
D j K j arg |
|
|
arg |
F j arg |
D j |
|
0 |
0 |
0 |
|
n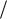 
2 n 2l 
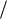2 l
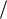2 2 .
отсюда следует формулировка критерия Найквиста. для устойчивости замкнутой
системы автоматического регулирования необходимо и достаточно, чтобы частотный |
||||
годограф |
частотной |
передаточной функции разомкнутой системы Wp j |
при |
|
изменении |
от |
0 |
до охватывал l 2 раз в положительном направлении точку |
|
1, j0 , где l - |
число корней характеристического уравнения разомкнутой системы, |
|||
лежащих в правой полуплоскости. очевидно, что формулировка критерия Найквиста для первого случая является частным случаем ( l 0 ) только что приведенной формулировки.
III случай – система в разомкнутом состоянии находится на границе устойчивости ( 1) или неустойчива ввиду наличия нескольких нулевых корней ( 1)
Передаточная функция системы в разомкнутом состоянии
Wp p K p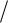 
p D1 p ,
где - число нулевых корней характеристического уравнения системы в разомкнутом состоянии; K p и D1 p - полином от p , причем D1 p не имеет нулей в правой полуплоскости и на мнимой оси.
В этом случае нельзя пользоваться приведенными выше формулировками критерия Найквиста, поскольку принцип аргумента, положенный в основу критерия Найквиста, не
рассматривает варианты, когда корни находятся на мнимой оси. При |
0 значение |
||
Wp j , и поэтому невозможно |
судить, |
охватывает годограф |
Wp j точку |
1, j0 или нет. |
|
|
|
Путём искусственного сдвига |
нулевых |
корней ( pi ) |
с последующим |
предельным переходом 0 рассматриваемый случай можно к первому или второму
случаям, что даст возможность применить приведенные формулировки критерия Найквиста.
сведем |
рассматриваемую систему |
к |
|||
системе, |
устойчивой |
в |
разомкнутом |
||
состоянии ( pi |
). возьмем для простоты |
||||
вначале |
систему при |
1 и |
запишем |
ее |
|
измененную |
передаточную |
функцию |
в |
||
разомкнутом состоянии: |
|
|
|||
Рис. 5
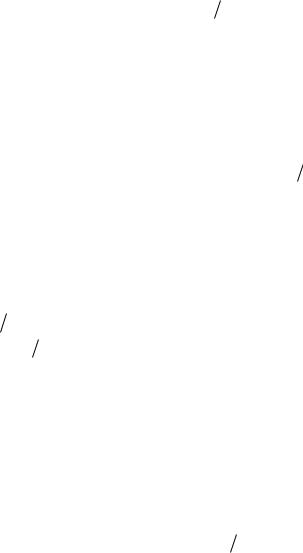
W p |
K p |
|
|
1 |
|
K p |
. |
|
p D1 p |
|
p 1 D1 p |
||||||
p1 |
|
|
|
|||||
|
|
|
|
|
|
|
||
На рис. 5, а показано, как сместился нулевой корень характеристического уравнения разомкнутой системы: она стала устойчивой. При этом интегрирующее звено
превратилось в инерционное с постоянной времени и коэффициентом усиления, равным
1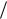
.
Частотная передаточная функция разомкнутой системы |
||||||||||
W |
|
j |
K j |
|
|
1 |
|
K j |
|
. |
p1 |
j D1 j |
|
j 1 D1 j |
|||||||
|
|
|
|
|
||||||
|
|
|
|
|
||||||
На рис. 5, б показаны частотные годографы Wp j и Wp1 j соответственно |
||||||||||
сплошной и штриховой линиями. они близки друг к другу на высоких частотах и |
|||||||||
отличаются на низких частотах: |
годограф |
Wp j |
при |
0 |
уходит |
вниз в |
|||
направлении отрицательной мнимой полуоси, годограф Wp1 j при |
0 проходит |
||||||||
через IV |
квадрант |
и попадает на |
действительную положительную |
полуось |
в точку |
||||
k , j0 , |
где k |
- |
коэффициент усиления исходной |
разомкнутой |
системы, |
равный |
|||
K j0 D1 j0 . При |
0 оба годографа совпадают на всех частотах, кроме 0: |
||||||||
годограф |
Wp1 j |
отличается от |
Wp j |
наличием |
дуги |
бесконечного |
радиуса, |
||
проходящей через IV квадрант и приводящей годограф при 0 к действительной положительной полуоси (рис. 5, в). Будем называть эту часть годографа "дополнением в бесконечности".
Аналогично строятся измененные частотные годографы при
2 дополнение в бесконечности проходит через два квадранта, а для произвольного значения дополнение годографа в бесконечности представляет собой дугу бесконечно
большого радиуса, начинающуюся при |
0 на действительной оси и с увеличением |
частоты описывающей угол 2 |
в отрицательном направлении вокруг начала |
координат (рис. 5, г). |
|
Для частотных годографов разомкнутых систем, дополненных в бесконечности, можно пользоваться первой формулировкой критерия Найквиста. Для устойчивости замкнутой системы автоматического регулирования необходимо и достаточно, чтобы
частотный годограф разомкнутой системы Wp j при изменении от 0 до не
охватывал точку 1, j0 . Эта же формулировка действительна при наличии пар чисто мнимых корней у характеристического уравнения разомкнутой системы.
Показанные на рис. 5 годографы соответствуют: на рис. 5, б - устойчивой системе;
на рис. 5, в - |
неустойчивой системе; рис. 5, г при 2 - устойчивой, а при |
3 - |
неустойчивой системе. |
|
|
Понятие |
"охват точки 1, j0 ", которое используется в приведенных выше |
|
формулировках критерия Найквиста, имеет некоторую неопределенность. Действительно,
есть случаи, когда трудно сразу сказать, охватывает или не охватывает эту точку годограф |
||||
Wp j . |
Поэтому существует иная формулировка критерия Найквиста, |
основанная на |
||
подсчете |
числа переходов |
частотного |
годографа Wp j через |
отрицательную |
действительную полуось от |
1 до . |
Причем пусть переход будет положительным, |
||
если при возрастании годограф переходи из верхней полуплоскости в нижнюю, и отрицательным, если годограф переходит из нижней полуплоскости в верхнюю (рис. 6).
Общая формулировка критерия Найквиста охватывает все три рассмотренных выше случая.
Для устойчивости замкнутой системы автоматического регулирования необходимо и достаточно, чтобы разность между числами положительных и отрицательных переходов
частотного годографа разомкнутой системы Wp j (АФЧХ разомкнутой системы) через
отрицательную действительную ось от 1 до была равна l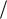
2 , где l - число корней характеристического уравнения разомкнутой системы, лежащих в правой полуплоскости.
Показанный на рис. 6, а годограф Wp j при l 0 соответствует устойчивой
замкнутой |
системе; |
на рис. 6, б показан |
|
годограф |
Wp j |
неустойчивой |
в |
разомкнутом состоянии системы, для которой
l 2 . годограф имеет два положительных перехода и один отрицательный переход, следовательно, разница между числами переходов равна единице. Согласно приведенной выше формулировке критерия устойчивости рассматриваемая система устойчива в замкнутом состоянии.
Если в системе имеются местные обратные связи, то необходимо убедиться в том, что по цепи местной обратной связи не нарушена устойчивость при разомкнутой главной обратной связи. Проверка устойчивости цепи местной обратной связи может быть сделана посредством использования любых критериев устойчивости, в том числе и посредством критерия Найквиста. В случае, если для местной обратной связи будет получено указание на ее неустойчивость, необходимо определить число корней, лежащих в правой полуплоскости.
Помимо исследования устойчивости по виду АФЧХ разомкнутой системы можно оценить и некоторые качественные показатели замкнутой системы, например, запас устойчивости. Более того, появляется возможность указать, как и за счет каких средств неустойчивая замкнутая система может быть сделана устойчивой и как можно повысить качество устойчивой замкнутой системы.
Тема 3.6. Качество процессов управления и методы его исследования
Показатели качества
1. Отношение максимального (пикового) значения АЧХ к её значению при нулевой частоте получило название частотного показателя колебательности:
M A рез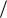 
A 0 .
Здесь применяется понятие резонансной частоты рез , соответствующей экстремуму Amax или, иначе говоря, резонансному пику АЧХ, т.е.
Amax = A рез .
2. Запас устойчивости по фазе замкнутого контура линейной системы с единичной отрицательной обратной связью вычисляется по формуле:
раз ср .
Применяется понятие |
частоты среза cр , соответствующей |
A cр 1 или |
||
L 20 lg A 0 . |
|
|
||
3. Запас устойчивости по амплитуде замкнутого контура линейной системы с |
||||
единичной отрицательной обратной связью вычисляется по формуле: |
|
|||
h 1 Aраз |
|
раз |
. |
|
|
|
|||
|
|
|
|
|
|
и h характеризуют удаление кривой Wраз jω от критической точки 1; j0 . |
4. |
Степень устойчивости определяется расстояние до ближайшего к мнимой |
оси корня (или пары комплексно-сопряженных корней) характеристического уравнения системы.
5. Степень колебательности max |
Im si |
|
, где s |
|
- ближайший к мнимой оси |
|
Re si |
i |
|||||
|
|
|
|
|||
|
|
|
|
|
корень (или пара комплексно-сопряженных корней) характеристического уравнения системы.
6. Время регулирования tр - это показатель качества, оценивающий длительность переходного процесса. Поскольку в идеальной линейной системе переходный процесс бесконечен, поэтому временем регулирования t р считают тот промежуток времени, по истечении которого отклонения выходной координаты САУ y t от установившегося значения yуст не превышают допустимого значения yуст
y yуст yуст.
Вбольшинстве случаев yуст 5%.
Всвою очередь, yуст можно рассчитать, исходя из теоремы операционного
исчисления – теоремы о предельном значении оригинала –
lim f t lim pF p ,
t |
p 0 |
|
|
|
|
|
т.е. yуст lim y t lim pY p . |
|
|
|
|||
t |
p 0 |
|
|
|
|
|
7. Время |
нарастания |
tн |
– |
время между |
моментами |
приложения входного |
воздействия и первым пересечением кривой переходного процесса (кривой разгона) y t |
||||||
границ "трубки" допустимых отклонений yуст. |
|
|
||||
8. Перерегулирование |
|
– |
оценивают как |
разность |
между максимальным |
|
значением hmax переходной характеристики и ее установившемся значением yуст :
ymax yуст 100%.
yуст
9. Статическая погрешность ст - показатель качества автоматической системы,
который характеризует относительную разность между действительным и требуемым значением регулируемой координаты в установившемся режиме и вычисляется по формуле:
ст |
|
|
yуст g t |
|
|
, |
|
|
|
||||||
|
|
|
|
|
|||
|
g t |
|
|
|
|||
|
|
|
|
|
|
|
|
где y t - |
выходная |
координата САУ (регулируемая координата); g t - задающее |
|||||
воздействие, определяющее требуемой значение регулируемой величины.
Для определения вынужденной (установившейся) ошибки используется
X p |
x p |
1 |
|
, |
||
|
|
|
|
|||
G p |
|
1 W p |
||||
|
|
|||||
где x p передаточная функция замкнутой системы по ошибке, W p - передаточная функция разомкнутой системы.
Формула для вынужденной ошибки
x |
уст |
c g(t) c |
dg(t) |
|
c2 |
|
d 2 g(t) |
|
|
|
|
|
|||||||
|
0 |
1 |
|
2! dt2 |
|||||
|
|
|
|
dt |
|
||||
Величины c0 , c1, c2 , называют коэффициентами ошибок, которые могут
определяться согласно общему правилу разложения в ряд Тейлора c0 x p p 0 ,
|
d |
x |
p |
|
|||||
c |
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
||||
1 |
|
dp |
|
|
|
|
|||
|
|
|
|
p 0 |
|||||
|
|
|
|
|
|
|
|
|
|
|
d m |
|
|
p |
|||||
|
|
|
|
|
x |
|
|
|
|
cm |
|
|
|
|
|
|
. |
||
dp |
m |
||||||||
|
|
|
|
|
p 0 |
||||
10. Порядок астатизма систем автоматического управления.
Система с нулевым порядком астатизма по данному воздействию, или
статическая система, |
- система, вынужденная ошибка которой |
в режиме отработки |
||||||||
постоянного задающего воздействия |
g t A0 1 t |
не равна нулю и пропорциональна |
||||||||
величине этого воздействия. Это может иметь место только при c0 x p p 0 0 . |
||||||||||
Система с астатизмом первого порядка - система, вынужденная ошибка которой |
||||||||||
в режиме |
отработки |
постоянного задающего |
воздействия |
равна нулю, т.е. |
||||||
c0 x p |
p 0 0 , |
а при отработке линейно изменяющегося во времени задающего |
||||||||
воздействия |
g t A0 |
A1t 1 t постоянна и пропорциональна |
A1 . Это может иметь |
|||||||
|
|
d |
x |
p |
|
|
|
|||
место только при c |
|
|
|
|
0 . |
|
|
|||
|
|
|
|
|
|
|||||
|
1 |
|
dp |
|
|
|
|
|||
|
|
|
p 0 |
|
|
|
||||
Таким образом, порядок астатизма системы равен номеру первого не равного нулю коэффициента ошибки по рассматриваемому воздействию.
11. Интегральные оценки
Интегральные оценки имеют целью дать общую оценку быстроты затухания и величины отклонения управляемой величины в совокупности, без определения того и другого в отдельности. Простейшей интегральной оценкой может служить величина