
TAU_OsipovaEA
.pdf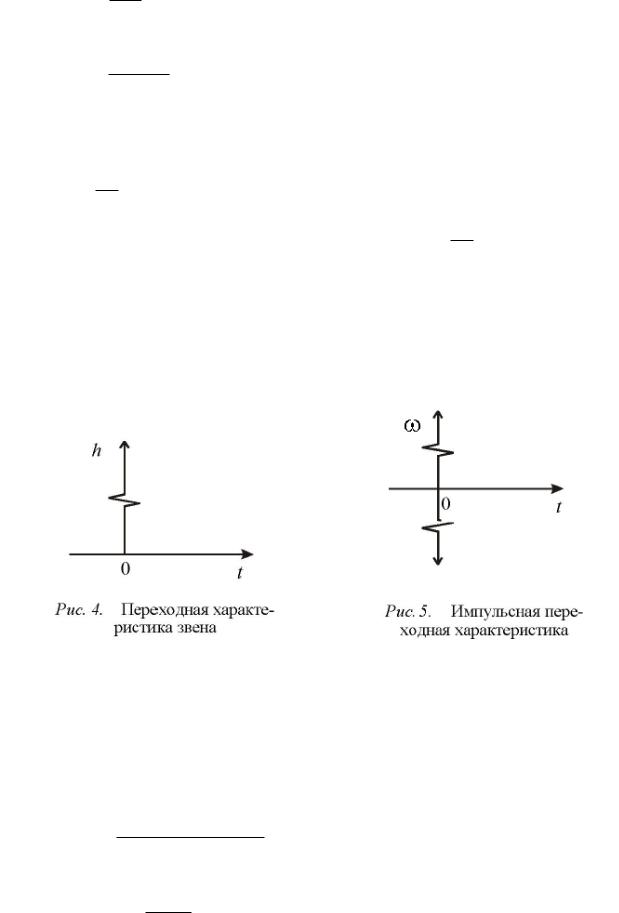
xвых k dxdtвх .
Его передаточная функция имеет вид
W p X вых p kp. X вх p
Примером дифференцирующего звена часто может служить тахогенератор постоянного тока, если в качестве входной величины рассматривать угол поворота его ротора, а в качестве выходной-напряжение якоря
U k ddt ,
где k - коэффициент преобразования числа оборотов вала n t d в напряжение.
dt
Переходная характеристика дифференцирующего звена определяется выражением
h t k t ,
и имеет вид функции (рис. 4).
Импульсная переходная функция идеального дифференцирующего звена (рис. 5)
представляет собой «дуплет» функций
t k t .
Рассмотрим теперь частотные характеристики звена. Амплитудно-фазовая
характеристика |
|
W j jk |
|
совпадает |
с положительной мнимой полуосью комплексной плоскости; вещественная |
частотная |
характеристика равна 0, Re 0; мнимая частотная характеристика |
отсутствует выражению
Im k ,
т.е. представляет собой линейно нарастающую функцию. С ней совпадает амплитудная частотная характеристика, которая имеет вид
A 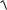
 Re 2 Im 2 Im
Re 2 Im 2 Im
Выражение для ФЧХ следующее:
arctg Im 0 при Re 0 Re при Re 0
k . .
2 .
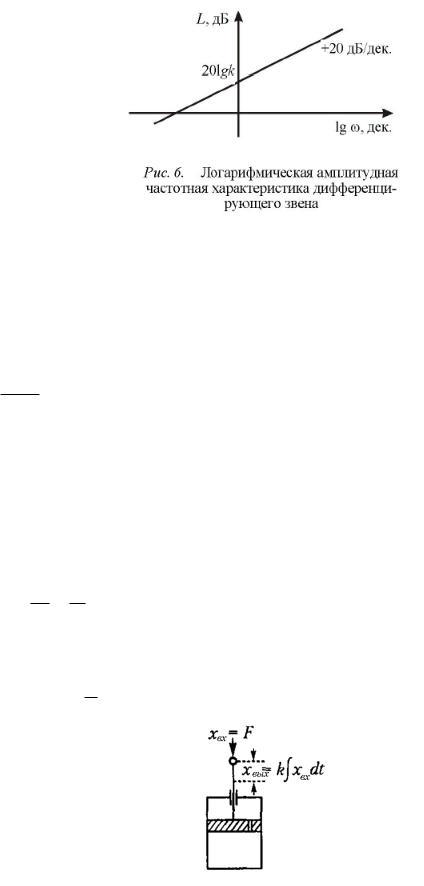
Следовательно, на всех частотах имеется постоянный фазовый сдвиг.
Логарифмическая частотная характеристика звена следующая:
L 20 lg A 20 lg k 20 lg .
Как видно из графика рис.6, идеальное дифференцирующее звено усиливает высокочастотные сигналы.
Интегрирующее звено
Интегрирующим называется звено, которое описывается дифференциальным уравнением
dxвых kxвх.
dt
Его передаточная функция имеет вид
W p |
X вых p |
|
k |
||||
|
|
|
|
|
. |
||
X |
вх |
p |
p |
||||
|
|
|
|
|
|
|
|
Примером интегрирующего звена может служить гидравлический демпфер (рис.7), если в качестве входной величины рассматривать силу F , действующую на поршень, а в качестве выходной-перемещение поршня. Так как скорость движения поршня пропорциональна приложенной силе (без учета инерционных сил)
dxdt FS ,
где S - коэффициент скоростного сопротивления; его перемещение будет пропорциональным интегралу от приложенной силы:
x dt S1 Fdt.
Рис. 7. Гидравлический демпфер Переходная характеристика звена имеет вид линейно возрастающей функции
t
h t k 1 d kt1 t ,
0
а импульсная переходная функция – ступенчатой функции
t
t k d k1 t .
0
Выражение для АФЧХ (рис. 8) получим,
заменив в передаточной функции p на |
j : |
|||||
W j |
k |
j |
k |
. |
|
|
|
|
|
||||
|
j |
|
|
|
||
Вещественная |
частотная характеристика |
|||||
отсутствует, |
Re 0. Мнимая |
частотная |
||||
характеристика имеет вид
Im k ,
а амплитудная частотная характеристика
A k .
При этом фазовая частотная характеристика следующая:
arctg Im 0 при Re 0 Re при Re 0
т.е. звено имеет постоянный фазовый сдвиг, который не зависит от частоты.
АФЧХ интегрирующего звена имеет вид прямой, совпадающей с отрицательной мнимой полуосью комплексной плоскости.
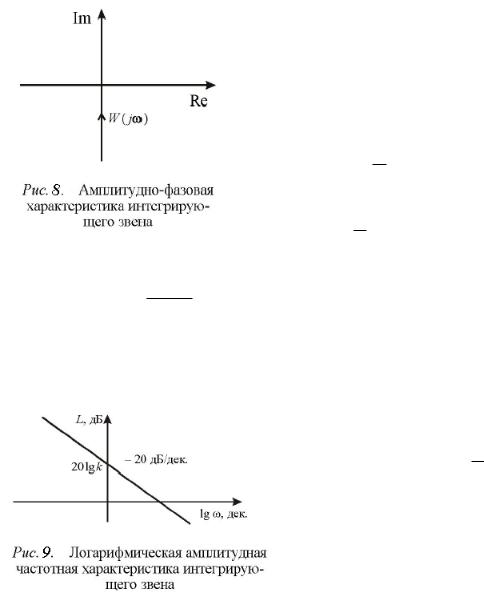
Запишем выражение для логарифмической амплитудно-частотной характеристики
L 20 lg A 20 lg k 20 lg k 20 lg ,
и изобразим ее график (рис. 9).
Как видим, ЛАЧХ интегратора представляет собой прямую с наклоном20дБ/дек и пересекает ось ординат в точке 20 lg k . Она показывает, что звено усиливает
низкочастотные |
сигналы |
и |
ослабляет |
высокочастотные.
Тема 2.4. Алгебра передаточных функций
Для определения передаточных функций автоматических систем по их структурным схемам необходимо уметь определять передаточные функции соединений элементов по передаточным функциям отдельных элементов. При рассмотрении структурной схемы нетрудно выделить три характерных соединения: последовательное, параллельное и обратное. Правила, позволяющие определять передаточные функции системы в целом по передаточным функциям отдельных элементов, и составляют алгебру передаточных функций.
1. Последовательное соединение. Последовательным соединением элементов называется такое соединение, при котором выходная величина предшествующего
элемента является входной величиной последующего (рис.1).
|
|
|
|
|
|
|
|
|
|
|
|
Рис.1 |
|
||
Для последовательного соединения имеем |
|
||||||||||||||
X 2 |
p W1 |
p X1 p , |
|
|
|
|
|||||||||
X 3 |
p W2 |
p X 2 p , |
|
|
|
|
|||||||||
отсюда после исключения X 2 p получаем |
|
||||||||||||||
X 3 p W2 p W1 p X1 p W p X1 p , |
|||||||||||||||
и, значит, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W p W1 |
p W2 p . |
|
|
|
|
||||||||||
В общем случае при последовательном соединении n элементов |
|||||||||||||||
W p W1 |
p W2 p Wn p . |
|
|||||||||||||
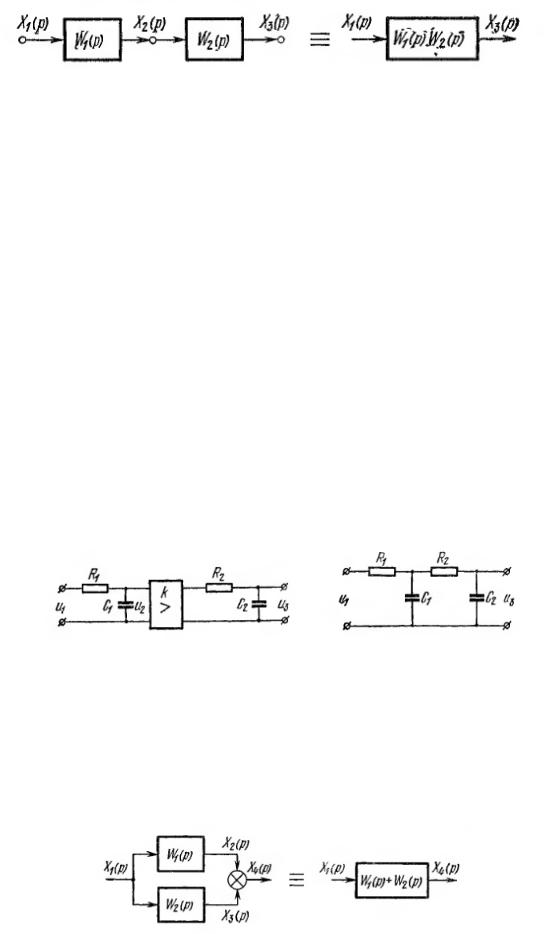
Пример. Последовательное соединение RC-цепей (рис.2). Передаточные функции |
|||||||||||||||
RC-цепей имеют вид |
|
|
|
|
|
|
|
|
|||||||
W1 p |
|
|
1 |
|
,T1 |
R1C1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||
T1 p 1 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W2 |
p |
|
|
|
1 |
|
|
|
,T2 |
R2C2 |
, |
|
|
||
|
|
|
|
|
|
|
|
|
|||||||
T2 p 1 |
|
||||||||||||||
|
|
|
|
|
|
|
|
||||||||
k коэффициент |
усиления усилителя, включенного между RC-цепями. Передаточная |
||||||||||||||
функция такого последовательного соединения будет равна |
|||||||||||||||
W p W1 p W2 p |
|
k |
. |
||||||||||||
|
|
|
|||||||||||||
T1 p 1 T2 p 1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рис.2 Рис.3 При отсутствии «развязывающего» усилителя передаточная функция
последовательного соединения RC-цепей (рис. 3) уже не определяется вышеприведенным выражением, поскольку подсоединение второй RC-цепи «нагружает» первую и, следовательно, напряжение на выходе первой цепи изменяется. Только при достаточно большом входном сопротивлении второй RC-цепи последовательное соединение (рис. 3) приближенно определяется вышеприведенным выражением.
2. Параллельное соединение. Параллельным соединением элементов называется такое соединение, при котором входная величина одна и та же для всех элементов, а выходные величины суммируются (рис. 4).
Рис. 4
Для параллельного соединения имеем
X 2 p W1 p X1 p ,
X3 p W2 p X1 p ,
X 4 p X 2 p X3 p .
Из чего получаем
X 4 p (W1 p W2 p ) X1 p W p X1 p .
А, значит,
W p W1 p W2 p .
В общем случае при параллельном соединении n элементов
W p W1 p W2 p Wn p .
|
Пример. Соединение малоинерционной и инерционной термопар |
||||||
(рис. 5). Обозначим через |
k1 и k2 коэффициенты передачи термопар |
||||||
|
градус , а через |
T |
и T |
|
- их постоянные времени, причем T T . |
||
|
|
|
1 |
|
2 |
1 |
2 |
|
вольт |
|
|
|
|
|
|
Передаточные функции термопар имеют вид |
|
||||||
W1 p |
k1 |
|
, W2 |
p |
k2 |
|
. |
|
T1 p 1 |
T2 p 1 |
|||||||
|
|
|
|
|||||
Э.д.с. термопар алгебраически складываются, поэтому
W p W p W p |
(k1T2 k2T1 ) p k1 k2 |
. |
||||
|
||||||
1 |
2 |
|
|
T1 p 1 T2 p 1 |
||
|
|
|
|
|||
В частном случае, при k1 k2 |
k, |
|||||
W p |
k(T2 |
T1 ) p |
|
|
||
|
. |
|
|
|||
T p 1 T p 1 |
|
|
||||
1 |
2 |
|
|
|
|
|
Такое соединение термопар приобретает новые свойства, а именно свойства дифференцирующего устройства.
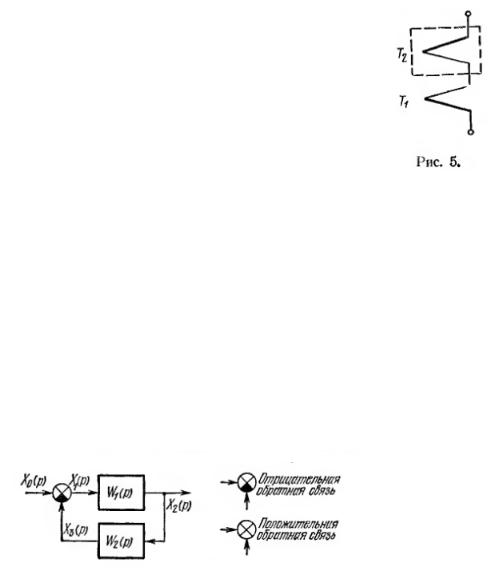
3. Обратное соединение. Обратным соединением двух элементов или соединением обратной связи называется такое соединение, при котором выход каждого из элементов соединяется со входом другого элемента (рис. 6).
Рис. 6
Для обратного соединения имеем
X 2 p W1 p X1 p ,
X3 p W2 p X 2 p ,
X1 p X0 p X3 p .
Знак минус в последнем уравнении соответствует отрицательной обратной связи, а знак плюс – положительной обратной связи.
Из чего получаем
Wзам p |
|
|
W1 p |
|
. |
|
1 |
W1 p W2 p |
|||||
|
|
|||||
Элемент, |
|
характеризуемый передаточной функцией W1 p , назовем прямой |
||||
частью замкнутой системы, а элемент, характеризуемый W2 p , - обратной связью.
Пример. Система посадки самолета. В данном случае у пилота три основных задачи:
1. самолет должен приближаться к аэродрому, выдерживая курс по центру посадочной полосы.
Центр
посадочной
полосы
2.соблюдение надлежащей глиссады (траектории полета самолета, вертолета, планера при снижении).
3.выдерживание правильной скорости.
Рассмотрим одну из этих задач – задачу удерживания самолета по центру |
|||||
посадочной полосы (задачу управления горизонтальным положением самолета). |
|||||
Функциональная схема системы, решающей данную задачу, можно представить в |
|||||
виде |
|
|
|
|
|
|
|
Самолет |
|
|
|
Заданное |
|
|
|
Горизонтальное |
|
|
Элероны и |
Фюзеляж |
положение |
||
положение |
|
||||
Регулятор |
механизм |
||||
самолета |
|
||||
|
управления |
|
|||
+ |
|
|
|
||
- |
|
|
|
||
|
|
|
|
||
|
|
Датчики |
|
|
|
Пилот |
|
|
|
|
|
Элероны – аэродинамические органы управления, в первую очередь предназначенные для управления углом крена самолета, т.е. углом поворота самолета вокруг его продольной оси, представляемой собой специальные плоскости в задней части каждого крыла.
Фюзеляж – корпус летательного аппарата.
Предполагается, что горизонтальное положение самолета регулируется с помощью элеронов. На самом деле для управления горизонтальным положением самолета используется также руль поворота, но мы для простоты ограничимся элеронами. Элероны в совокупности с механизмами, изменяющими угол наклона, образуют исполнительное устройство системы управления.
Вданной системе пилот использует несколько датчиков для определения горизонтального положения самолета. Он оценивает положение самолета относительно центра посадочной полосы с помощью панели управления в кабине самолета и визуально. Таким образом, пилот знает желаемое горизонтальное положение самолета и имеет информацию о действительном положении. Он управляет элеронами так, чтобы самолет занял желаемое положение. В терминах систем управления обычно разность между желаемым и действительным положением называют ошибкой системы.
Вданной системе функции регулятора выполняет пилот, который также выполняет функции датчика. Качество выполнения пилотом этих действий зависит от степени его тренированности. Целью тренировок является при каждой посадке при одних и тех же обстоятельствах принимались одни и те же действия.
Рассмотрим теперь автоматическую систему посадки самолета, в которой пилот не принимает участие. Система автоматической посадки также может быть представлена тем же рисунком, только элеронами здесь управляет автопилот, который в свою очередь является замкнутой системой управления. Роль датчика обычно выполняет радар, который определяет положение самолета относительно центра посадочной полосы. Функции регулятора выполняют цифровой компьютер, который решает систему уравнений и вырабатывает команды, подаваемые на автопилот.
Правила переноса
Тема 2.5. Получение уравнений состояний по математической модели «входвыход»
Раздел 3. Анализ систем управления Тема 3.1. Задачи анализа систем управления
Тема 3.2. Понятие устойчивости. Устойчивость возмущенного и невозмущенного движения по А.М. Ляпунову
Всякая система автоматического управления должна быть прежде всего устойчивой. В противном случае она будет неработоспособной, так как любое воздействие на такую систему вызывает недопустимое возрастание физических величин, характеризующих работу системы (токи, электрические напряжения, механические напряжения и т.д.).
Устойчивой будем считать систему, если после прекращения действий возмущающих сил, вызвавших отклонения движения системы от заданного, система стремится вернуться к исходному заданному движению.
Говоря об устойчивости системы, обычно, подразумевают устойчивость ее состояния равновесия. В других случаях подразумевают устойчивость заданного движения системы, принимаемого за невозмущенное движение. Так как равновесие – это частный случай движения, то вышеизложенное определение понятия устойчивости формулируется применительно к движению.
Методы теории устойчивости Александра Михайловича Ляпунова пригодны как для исследования устойчивости при постоянно действующих возмущениях (возмущенное движение), так и для невозмущенного движения по отношению к возмущениям начальных условий.
Пусть в фазовом пространстве состоянию равновесия соответствует положение изображающей точки в начале координат qk 0 .
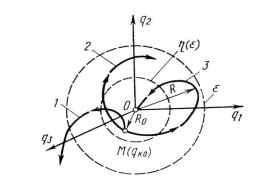
Рис. 1
Получив в момент времени t t0 начальные возмущения qk 0 , система, предоставленная самой себе, будет совершать возмущенное движение. В фазовом пространстве Rq n этому движению будет соответствовать возмущенное движение
изображающей точки.
Можно взять какое-либо уравнение q1, q2 , , qn R и рассматривать его, как уравнение некоторой поверхности в фазовом пространстве Rq n . Например, уравнение
q2 |
q2 q2 q2 R2 , |
|
||||
1 |
|
2 |
3 |
|
n |
|
будет уравнением сферы в фазовом пространстве, а R - расстояние изображающей |
||||||
точки M |
q1, q2 , , qn на поверхности этой сферы от начала координат. В таком случае |
|||||
неравенство |
q2 |
q2 |
q2 |
q2 R2 |
будет определять область, расположенную |
|
|
|
1 |
2 |
3 |
n |
|
внутри сферы. |
|
|
|
|
||
Возмущенное движение может протекать при t 0 таким образом, что с течением |
||||||
времени: |
|
|
|
|
|
|
1) |
|
изображающая точка M всё дальше удаляется от начала координат так, что |
||||
|
|
|
n |
|
|
|
величина R2 qk2 |
растет неограниченно (рис. 1, кривая 1); |
|||||
|
|
k 1 |
|
|
|
|
2) |
|
изображающая |
точка M остается внутри некоторой окрестности начала |
|||
n
координат, так что величина R2 qk2 во время движения системы имеет ограниченное
k 1
значение, не превосходящее наперед заданного малого положительного числа , то есть
R2 (рис. 1, кривая 2);
3) изображающая точка M с течением времени возвращается в начало координат, совершая около него затухающие колебания, так что в конце концов величина
R2 становиться равной нулю, то есть lim R2 |
0 (рис. 1, кривая 3). |
t |
|
В двух последних случаях равновесное состояние системы можно считать устойчивым, поскольку система, получив начальное возмущение, в дальнейшем в течение всего времени возмущенного движения продолжает оставаться в ближайшей окрестности равновесного состояния или же снова возвращается в это состояние.
Чтобы придать словам «продолжает оставаться в ближайшей окрестности» конкретный смысл, А.М. Ляпунов предложил следующее определение устойчивости равновесия системы.
Равновесие системы, определяемое в фазовом пространстве Rq n значениями переменных qk 0 , будет устойчивым относительно величин qk , если для всякого
заданного положительного числа |
, как бы мало оно ни было, |
можно найти другое, |
||||||||
зависящее от , положительное |
число |
(эта) такое, что для всех начальных |
||||||||
возмущений системы, удовлетворяющих при t t0 условию |
|
|||||||||
|
|
, k |
|
|
, |
|
|
|
||
|
qk 0 |
1, n |
|
|
(1) |
|||||
в возмущенном движении |
при t 0 |
переменные qk |
будут удовлетворять |
|||||||
неравенствам |
|
|
|
|||||||
|
qk t |
|
|
|
|
|||||
|
, k |
1, n |
. |
|
|
(2) |
||||
Если хотя бы одно из неравенств (2) не выполняется, то равновесие системы неустойчиво. Неравенства (1) ограничивают область допустимых начальных отклонений от положения равновесия. Неравенства (2) ограничивают область протекания возмущенного движения. Если возмущенное движение таково, что система в конце
концов возвращается к прежнему равновесному состоянию, то есть если lim qk t 0 , то
t
равновесие системы будет устойчивым асимптотически.
Геометрически (рис.1) приведенное определение устойчивости равновесия системы означает следующее. Равновесие системы qk 0 будет устойчивым, если для всех
начальных отклонений системы qk 0 от положения равновесия, не выходящих за границу
сферы , окружающей начало координат, то есть при |
|
n |
, |
t 0 , |
qk20 |
||
|
|
k 1 |
|
возмущенное движение системы при t 0 не будет достигать границы сферы , то есть
n
будет выполняться неравенство qk2 t .
k 1
Аналогично всему вышеизложенному определяется по Ляпунову устойчивость невозмущенного движения.
Если для любых сколь угодно больших начальных отклонениях, принадлежащих области, которая задается уравнениями движения системы управления, система после снятия возмущений продолжает оставаться в ближайшей окрестности равновесного состояния или же снова возвращается к прежнему равновесному положению, то невозмущенное движение системы называется устойчивым «в целом».
Если же выполнение условий устойчивости требует дополнительного ограничения начальных отклонений системы конечными значениями, то невозмущенное движение называется неустойчивым «в большом».
Если условия устойчивости выполняются лишь при сколь угодно малых отклонениях, то говорят об устойчивости «в малом».
Тема 3.3. Корни характеристического уравнения и устойчивость линейной динамической системы
Вопрос об устойчивости системы сводится к выяснению устойчивости свободного движения системы и требует анализа характера решения свободного движения, то есть общего решения уравнения без правой части.
Если свободная составляющая управляемой переменной, которая вызвана ненулевыми начальными условиями, с течением времени стремится к нулю, то такую систему называют устойчивой (асимптотически устойчивой).
Если свободная составляющая стремится к некоторому конечному значению или совершает гармонические колебания, амплитуда которых стремится к некоторому конечному значению, то такую систему называют нейтральной (нейтрально устойчивой).
Если свободная составляющая управляемой переменной неограниченно возрастает или совершает гармонические колебания с неограниченно возрастающей амплитудой, то
такую систему называют неустойчивой.
Уравнения свободного движения системы может быть приведено к виду
a |
d n y |
a |
d n 1 y |
... a |
dy |
a y 0, |
(1) |
|
|
|
|||||
n dtn |
n 1 dtn 1 |
1 dt |
0 |
|
|||
где n -порядок уравнения системы, ai - коэффициенты, определяемые из параметров системы.
Линейное однородное ДУ (1) имеет общее решение вида |
|
|
|
|
|
||||||||||||||||||||
y |
общ |
t C e p1t |
C |
2 |
e p2t |
C |
n |
e pnt , |
|
|
|
|
(2) |
|
|
|
|||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где C1,C2 , ,Cn |
- |
постоянные |
|
интегрирования; |
|
p1, p2 , , pn |
- |
корни |
|||||||||||||||||
характеристического уравнения свободного движения вида |
|
|
|
|
|
|
|||||||||||||||||||
a |
n |
pn a |
n 1 |
pn 1 |
... a p a |
0 |
0. |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Корни характеристического уравнения могут быть либо вещественными, либо |
|||||||||||||||||||||||||
комплексными попарно сопряженными. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
В |
|
случае |
вещественных |
корней |
|
обозначим |
pi |
i . |
Тогда |
общее |
|
решение |
|||||||||||||
уравнения (1) представляется как сумма n решений вида |
y |
t C |
e it . |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
i |
|
|
|
|
Общее решение еще называют переходной составляющей и система будет |
|||||||||||||||||||||||||
называться устойчивой, если с течением времени при |
t |
эта |
переходная |
||||||||||||||||||||||
составляющая будет стремиться к нулю: |
yобщ t 0 . |
|
|
|
|
|
|
|
|
||||||||||||||||
Каждая составляющая общего решения стремится к нулю лишь при отрицательном |
|||||||||||||||||||||||||
значении вещественного корня, то есть при i 0 . |
|
|
|
|
|
|
|
|
|||||||||||||||||
Комплексные корни имеют вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
pk |
k j k , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где k - вещественная часть комплексного корня; k |
- мнимые части корней. |
|
|||||||||||||||||||||||
Каждой паре комплексно-сопряженных корней будет соответствовать решение: |
|||||||||||||||||||||||||
y |
k |
t B cos |
k |
t C sin |
k |
t e k t , |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где B,C - постоянные интегрирования. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Движение, описываемое уравнением (1) будет сходящимся, если при |
t |
||||||||||||||||||||||||
решение |
|
yk t 0 . |
Это возможно лишь при отрицательном значении вещественной |
||||||||||||||||||||||
части комплексного корня.
Если корни изображать графически на комплексной плоскости, то:
1.Система асимптотически устойчива, если все корни ее характеристического уравнения лежат слева от мнимой оси.
2.Если все корни характеристического уравнения системы лежат слева от мнимой оси, и есть нулевые корни, то система нейтральная или находится на границе устойчивости.
При наличии одного нулевого корня pk 0 граница устойчивости называется апериодической. Соответствующая этому корню составляющая решения (2) Ck e pk t Ck , то есть переходная составляющая с течением времени стремится не к нулю, а к Ck .
В характеристическом уравнении нулевой корень появляется при a0 0.
При наличии пары чисто мнимых корней pk ,k 1 j k граница устойчивости
