
TAU_OsipovaEA
.pdfмомента попадания на дугу ВО, а в момент попадания на дугу ВО значение u переключается и становится равным 1.
Итак, согласно теореме 2, только описанные выше траектории могут быть оптимальными, причем из проведенного исследования видно, что из каждой точки фазовой плоскости исходит только одна траектория, ведущая в начало координат, которая может быть оптимальной (то есть задание начальной точки x0 однозначно определяет
соответствующую траекторию).
Полученное в рассмотренном примере решение оптимальной задачи истолковать следующим образом. Обозначим через x1, x2 x функцию, заданную на плоскости x1, x2 так:
1 ниже ллини АОВ и на дуге АО,x
1 выше ллини АОВ и на дуге ВО.
Тогда на каждой оптимальной траектории значение u t управляющего параметра (в произвольный момент t ) равно x t , то есть равно значению функции в той точке,
в которой в момент t находится фазовая точка, пробегающая оптимальную траекторию:
u t x t .
Это означает, что, заменив в системе (11) величину u функцией x , мы получим систему
1 |
|
|
|
|
||
|
dx |
x2 , |
|
|
|
|
|
dt |
|
(16) |
|||
|
|
|
||||
|
|
|
|
|||
dx2 |
|
|
||||
1 |
2 |
|
||||
|
|
x , x |
|
|
|
|
|
|
|
|
|
||
dt |
|
|
|
|
||
|
|
|
|
|||
решение которой (при произвольном начальном состоянии x0 ) дает оптимальную
фазовую траекторию, ведущую в начало координат. Иначе говоря, система (16) представляет собой систему дифференциальных уравнений (с разрывной правой частью) для нахождения оптимальных траекторий, ведущих в начало координат.
Тема 4.2. Метод логарифмических частотных характеристик Тема 4.3. Параметрический синтез систем
Всякая автоматическая система управления начинается с её проектирования и моделирования, после чего следует изготовление с необходимой наладкой, а затем передача в эксплуатацию и непосредственно эксплуатация.
Проектирование и наладка автоматической системы включает многие процедуры, среди которых важнейшими являются синтез и анализ САУ, в результате проведения которых выбираются параметры системы, обеспечивающие приемлемое качество управления. При этом процедура синтеза САУ заключается в последовательном решении двух задач: сначала осуществляется выбор закона регулирования, а затем определяются значения настроек регулятора. Кроме того, на практике чаще всего определение значений настроек регулятора требуется и в ходе эксплуатации, т. к. всегда имеют место постепенное изменение свойств объекта и технических средств регулирования, возможность возникновения непредвиденных изменений внешних условий и т.п.
Названные выше задачи являются соответственно задачами структурного и параметрического синтеза по тому или иному критерию качества. Поскольку они принципиально различны, при их решении применяются различные подходы. Понятно, что с точки зрения процесса решения задача структурного синтеза более сложна в сравнении с задачей параметрического синтеза.
Так при решении задачи структурного синтеза приходится иметь дело с формально неопределенными структурными связями, качественными критериями и неформальным описанием функционирования системы регулирования, что не позволяет в общем случае отнести решение этой задачи к классу формально разрешимых задач. Формальные методы структурного синтеза разработаны лишь для узкого круга задач; в широком смысле задача структурного синтеза неразрешима.
Суть параметрического синтеза заключается в нахождении таких значений вектора параметров настройки регулятора, при которых, с учётом заданных ограничений, принятый критерий качества регулирования имеет экстремальное значение. Причём один или несколько (случай многокритериальной оптимизация) критериев качества САУ выбираются исходя из экономических и технологических требований к качеству ведения процесса, а систему регулирования, обеспечивающую в данных конкретных условиях экстремум выбранному критерию качества при выполнении ограничений на заданный запас устойчивости и робастность, называют оптимальной.
Благодаря тому, что при решении вышеозначенной задачи предполагается, что структура автоматической системы определена, а определяемые параметры имеют метрическое выражение, задачу относят к классу формально разрешимых.
В системе управления, где структура определена, выбрать и установить настраиваемые параметры регулятора, обеспечивающие оптимальный (в общем случае близкий к оптимальному) процесс регулирования, можно, например, с помощью аналитических методов.
Такие методы приводят к явному формульному решению задачи без использования какихлибо итерационных или поисковых процедур. Важным их достоинством является то, что они позволяют судить об областях, а не об отдельных точках, в пространстве варьируемых параметров настройки регулятора, в которых автоматическая система будет обладать теми или иными свойствами. В инженерной практике подобный расчёт параметров САУ чаще всего базируются на классических частотных методах.
Важно подчеркнуть, что названные выше преимущества аналитических методов достигаются весьма дорогой ценой: ценой резкого ограничения возможностей. Так, например, практическое применение данных методов для расчёта импульсных САУ зачастую становиться возможным только после далеко идущей идеализации. Это, прежде всего, стало следствием того, что существующие методики получения расчётных формул для определения оптимальных параметров далеко не всегда позволяют связать достаточно простыми аналитическими зависимостями большинство критериев оптимальности с настраиваемыми параметрами регулятора. Но даже в тех случаях, когда применение аналитических методов принципиально возможно, возникают другие проблемы, которые тоже необходимо учитывать: во-первых, применение расчётных формул даже в простейших случаях, как правило, приводит к слишком громоздким выкладкам; во-вторых, следствием идеализации может стать неудовлетворительная работа реальной системы с найденными в результате расчётов параметрами регулятора .
Появление быстродействующих средств вычислительной техники способствовало бурному развитию методов организованного поиска приближенного решения экстремальных задач (т. е. численных методов оптимизации). Данные методы наряду с методами компьютерного моделирования позволяют решать такие задачи параметрической оптимизации систем управления, которые ранее представлялись невыполнимыми. Вместе с тем существуют и недостатки. Вопервых, в отличие от аналитических методов, численные методы оптимизации дают возможность определить положение оптимума, опираясь, прежде всего, на эксперимент, тем самым лишая полученные результаты общности. Во-вторых, применение численных методов оптимизации, как правило, сопровождается большим объёмом вычислений, главным образом связанного с необходимостью численного решения интегро-дифференциальных уравнений динамической системы для каждого сочетания настраиваемых параметров. Отметим, что интерес исследователей к последнему обстоятельству привел к появлению различных приёмов для уменьшения затрат вычислительных ресурсов.
Всоответствии с иной классификацией все методы поиска экстремума разделяют на два больших класса: поисковые и беспоисковые.
Впервом случае поиск оптимальных параметров настройки в процессе организации оптимального регулирования производится варьированием численных значений этих параметров с контролем изменения вызванного этими вариациями принятого критерия оптимальности. Это позволяет, априори зная только то, что критерий качества имеет экстремальный характер, определить направление движения к оптимуму и в конечном счете (если процедура сходится) достигнуть его. Разработано много алгоритмов такого поиска: генетический, Гаусса-Зайделя, Цилера-Никольса, деформируемого многогранника Нелдера-Мида, параметрического случайного поиска, многомерного сканирования и т. д. Простота поисковых алгоритмов и необходимость в минимальном объеме начальных сведений о системе регулирования делают их привлекательными для создания автоматических оптимизаторов. Но в то же время при реализации, как правило, наблюдается неодновременность настройки всех компонент вектора настраиваемых параметров и нарушение нормальных режимов работы объекта. Оба этих фактора снижают точность процесса оптимизации, и при наличии случайных помех и возмущений продолжительность его оказывается настолько велика, что часто делает поисковые методы неприемлемыми для практики. В лучшем случае алгоритмы таких методов могут применяться в обстановке медленного изменения критерия оптимальности, например, на окончательной стадии оптимизации, когда уже достигнута достаточно близкая к оптимуму область настройки.
Среди поисковых методов оптимизации лидирующее положение занимают генетические алгоритмы, которые на практике особенно часто используются для определения глобального оптимума при выбранном критерии оптимальности. Широкое распространение методов глобальной оптимизации обусловлено тем, что задачи оптимизации для весьма распространенных в настоящий момент сложных многоконтурных систем управления и систем управления с нейроконтроллерами, как правило, сопровождаются многоэкстремальностью функции цели. По существу, большая часть разновидностей генетического алгоритма является усложнением вероятностных методов оптимизации с повышенной плотностью вероятности размещения новых пробных точек в областях, где на предыдущем шаге критерий оптимальности оказался меньше. Соответственно, генетические алгоритмы унаследовали и ряд недостатков вероятностных методов: нет гарантии сходимости к глобальному оптимуму; не определена априори скорость сходимости и вычислительная сложность решения конкретной задачи; результат расчета существенно зависит от специфических настроек метода. Пожалуй, главным недостатком с точки зрения глобальной оптимизации систем автоматического регулирования является недостаточная обоснованность получаемых результатов. Связано это, прежде всего, с тем, что в технических задачах зачастую положение каждого локального оптимума независимо от других. В результате получение достоверного положения глобального оптимума оказывается невозможным без проверки значения критерия во всей области возможных изменений параметров настройки. Использование же генетического алгоритма для нахождения такого оптимума предполагает оценку рельефа критерия оптимальности через проверку лишь тех вариантов настройки, которые получаются случайным образом на первом шаге оптимизации и селекцией на последующих её шагах.
При промежуточном анализе результатов поиска применяют, например, метод Гаусса-Зайделя, когда система осуществляет поочередные адаптивные движения по переменным, причем каждый раз по одной из них при фиксированных значениях других. Данный метод очень прост в реализации, но без дополнительных усовершенствований непригоден вследствие большой погрешности и значительного времени поиска.
Метод многомерного сканирования – это еще один метод глобального многопараметрического поиска. В литературе отмечается универсальность и надежность этого метода, но большой объем вычислений часто заставляет переходить к более
экономичным с этой точки зрения методам, основанным на вычислении частных производных. При этом в работе установлено, что для ряда практически важных задач автоматического управления, в особенности при расчете многоконтурных систем с относительно небольшим числом настраиваемых параметров, большой объем расчетов, связанный с необходимостью многократного повторения расчетов по одному и тому же относительно простому алгоритму сканирования, учитывая быстродействие и объем памяти современных ЭВМ, является небольшой ценой получения оптимальных настроек. Кроме того, возможны различные модификации метода сканирования, которые позволяют существенно уменьшить объем вычислений, в том числе тогда, когда речь идет о поиске глобального экстремума в многоэкстремальных задачах.
В тех случаях, когда вычисление параметров регулятора производится на основе аналитического определения условий, обеспечивающих заданное качество регулирования, без применения специальных поисковых сигналов непосредственно на реальных системах, алгоритм поиска экстремума называют беспоисковым. Беспоисковые методы поиска экстремума предоставляют возможность избавиться от поиска как метода сбора информации для синтеза экстремального регулирования, что повышает быстродействие, точность и помехозащищенность, а так же делает разрешимой задачу оптимизации для ряда объектов, в которых недопустимы специальные пробные возмущения. Однако при этом требуется больший объем как априорной, так и рабочей информации об оптимизируемом процессе регулирования.
Раздел 5. Общие сведения о дискретных системах управления Тема 5.1. Понятия об импульсных и цифровых системах
Входные и выходные сигналы непрерывных систем являются функциями непрерывного времени t , т. е. независимая переменная t для всех сигналов системы принимает непрерывную последовательность значений. Если t принимает только конечное множество значений, то сигнал называется дискретным. На практике применение только непрерывных сигналов в САУ в иных случаях оказывается неэффективным или даже технически невозможным. В связи с этим наряду с непрерывным способом передачи и преобразования сигналов широко применяются дискретные способы, в которых используется представление непрерывного сигнала ее дискретными значениями, или, иначе говоря, квантование по уровню и/или по времени непрерывного сигнала в дискретный. Если САУ содержит, по крайней мере, один элемент, выходной сигнал которого определяется последовательностью выделенных значений
x1, x2 , ..., xn его входного сигнала и эта последовательность в общем случае бесконечна, то
такую систему называют дискретной. Тем самым в дискретные САУ включены автоматические системы, отличающиеся наличием разрывов того или иного, или тех или иных сигналов, например регулирующего воздействия, выходного сигнала исполнительного механизма, выходной величины измерительного устройства и т.п. В настоящее время существует общепринятая классификация дискретных систем по используемым в них видам квантования, согласно которым они подразделяются на релейные, импульсные и релейно-импульсные (цифровые).
Системы с квантованием по уровню называются релейными системами. В таких системах хотя бы у одного звена выходной сигнал изменяется скачком всякий раз, когда непрерывный входной сигнал достигает некоторых заранее фиксированных значений, называемых пороговыми. Такое звено называется релейным звеном.
Системы регулирования называются импульсными, если хотя бы один из сигналов, характеризующих состояние системы, квантуется по времени. Квантование по времени и модуляция осуществляются импульсным элементом (ИЭ). Входным сигналом такого элемента является непрерывным сигналом, а выходным - модулированная последовательность импульсов. При этом под модуляцией понимается изменение тех или
иных параметров импульсов в зависимости от выделенных в процессе квантования дискрет.
Система регулирования называется релейно-импульсной (цифровой), если она содержит цифровое устройство. В цифровом устройстве всегда имеет место квантование и по времени, и по уровню. Оттого естественным является повышенный интерес к вопросам теории дискретных систем в условиях быстрого развития микропроцессорных устройств и повсеместного использования их в системах управления технологическими процессами.
Широкое применение импульсных АСР в системах управления роботов и манипуляторов, в станкостроении, в авиационной, ракетно-космической, оборонной, транспортной, энергетической и других отраслях промышленности объясняется такими преимуществами, как:
1)возможность достаточно эффективно регулировать объекты с большой инерционностью и запаздыванием, подтверждением тому является накопившийся положительный опыт построения и эксплуатации экстремальных систем регулирования для большого числа инерционных производственных процессов;
2)высокая помехозащищенность. Указанное свойство системы регулирования относят к числу основных свойств, которое может характеризоваться средним значением ошибки (между требуемым и действительным значениями регулируемой величины), вызываемой возмущающими воздействиями или помехами. В импульсных системах высокие показатели помехозащищенности обусловлены тем, что непрерывное модулирующее воздействие заменяется решетчатой функцией и между двумя последовательными выборками возмущения не действуют на систему. Заметим, что проблема помехоустойчивости наиболее эффективно решается в классе широтноимпульсных систем, благодаря малому влиянию случайных вариаций амплитуды на информацию, содержащуюся в широтно-модулированной координате;
3)возможность использования исполнительного двигателя с бόльшим моментом вращения в течение короткого отрезка времени, что явно предпочтительнее использования двигателя с малым моментом вращения, но в течение более длительного времени. Кроме того, в случае импульсного регулирования можно ограничить величину момента вращения, развиваемую исполнительным двигателем, что подчас является главным требованием для предотвращения разрушения элементов системы;
4)существование условий как для передачи многих сигналов по одному каналу связи, так и для регулирования нескольких объектов с помощью одного импульсного регулятора. Такое поочередное использование оборудования для различных целей характерно для многоканальных САУ с их известными достоинствами;
5)повышенная точность и надежность системы, в т. ч. за счет возможности достаточно простыми средствами вводить в нужные моменты времени корректирующие воздействия;
6)простота реализации систем, малая энергоемкость, меньшие габаритные размеры
истоимость, в сравнении с непрерывными системами;
7)возможность достаточно легко согласовывать импульсные САУ с цифровыми вычислительными устройствами;
8)измерение физических величин, не нагружая объект, состояние которого характеризуется этой величиной, поскольку это измерение происходит периодически в течение малых промежутков времени;
9)возможность использования различных импульсных систем для описания и исследования моделей нейронных сетей, в которых, как известно, нейрон передает информацию в виде импульсов, и др.
Приведём их классификацию импульсных систем по используемым в них способам модуляции. Для этого, прежде всего, остановимся на характеристике последовательности
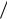
импульсов. Параметрами импульсной последовательности (несущей координаты)
являются амплитуда k -ого импульса |
Ak , период следования импульсов Tk (или частота |
|||
k 2 Tk ), их длительность kTk |
|
|||
k 1 , временнόе положение (фаза) переднего tk |
||||
|
|
|
|
ˆ |
или заднего фронта tk импульсов по отношению к тактовым точкам tk k 0,1, 2, ... , |
||||
таких что |
ˆ |
ˆ |
ˆ |
|
tk 1 |
tk Tk |
и t0 фиксировано. В периодических импульсных системах |
||
период Tk |
- величина постоянная, и для нее, как правило, вводят обозначение T . |
|||
Импульсную модуляцию различают по виду, роду и тактности модуляции.
Вид модуляции определяется в зависимости от того, какой параметр импульса (амплитуда, длительность, фаза, частота) модулируется непрерывным входным воздействием ИЭ. В связи с этим различают амплитудно–импульсную (АИМ), времяимпульсную (ВИМ) и комбинированную импульсную модуляции (КИМ). Причем под ВИМ понимается любой способ модуляции последовательности импульсов, при котором переменными параметрами являются один или несколько из ее временных признаков (временнόе положение импульса, момент определения его фронта). Из различных видов ВИМ наиболее распространенными являются широтно-импульсный (ШИМ), фазовый и частотный виды модуляции (ФИМ и ЧИМ). Таким образом, импульсные САУ в зависимости от вида импульсной модуляции подразделяются на амплитудно-импульсные системы (АИС), широтно-импульсные системы (ШИС), фазоимпульсные системы (ФИС) и т.д.
Обратим внимание на то, что среди импульсных систем линейной может оказаться только АИС в том случае, если непрерывная её часть не содержит нелинейных элементов. ШИС нельзя рассматривать как линейные даже в ограниченном диапазоне изменения регулируемой координаты, это делает их существенно нелинейными. В ИЭ, осуществляющем ШИМ, наблюдается два типа нелинейности: а) для него несправедлив принцип суперпозиции, т.е. реакция ИЭ на сумму входных воздействий не равна сумме реакций на каждое такое воздействие в отдельности; б) нелинейность, обусловленная ограничением максимальной ширины импульса, т.е. выходная характеристика ИЭ с ШИМ имеет насыщение.
В каждом из вышеперечисленных видов импульсной модуляции различают род модуляции, определения которого достаточно различны, но в их основу положено то, что род модуляции устанавливает временнóе соответствие значений модулирующей
координаты t и модулируемого параметра a t .
В соответствии с одной из существующих классификацией различают модуляцию первого и второго рода.
Пусть ak - значение модулируемого параметра, соответствующее k -ой тактовой точке ˆtk , k 0, 1, 2, .... Считается, что при модуляции первого рода ak определяется выборкой, взятой из координаты t только в фиксированный дискретный момент времени, соответствующий началу такта или сдвинутый относительно него на постоянную величину, и не зависит от изменения t между ними. В результате между значениями модулирующей координаты и модулируемого параметра можно наблюдать функциональную зависимость ak f ˆtk const , где 0 const Tk .
Импульсная модуляция второго рода характеризуется тем, что значения модулируемого параметра определяют не в фиксированных точках выборки, а некоторым
функционалом от модулирующей координаты t , определенной на конечном интервале времени (например, в течение времени действия импульса, т. е. когда
ˆ |
t |
|
ˆ |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
ˆ |
t |
, |
k 0, 1, 2, |
...). Для |
|||||||||
t t |
, t |
k |
k |
|
, или до его появления, когда t t |
k |
,t |
k |
|||||||||||||||||||||||||||
k |
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
||||||
каждого |
|
|
|
из |
указанных |
|
|
|
интервалов, |
соответственно, |
справедливы |
записи: |
|||||||||||||||||||||||
a f |
|
|
|
t |
|
|
|
t |
ˆ |
|
t , |
ˆ |
t |
|
или a |
f |
|
|
|
t |
|
|
|
|
|
ˆ |
ˆ |
t |
|
. Последние |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
t |
|
t |
|
k |
|
|
|
|
|
|
t t |
, t |
|
|
||||||||||||||||
k |
|
|
|
|
|
|
k |
k |
|
k |
|
|
k |
|
|
|
|
|
|
|
k |
|
k |
k |
|
|
|||||||||
означают, |
|
что |
на |
множестве |
|
M |
функций задан функционал, такой что каждой |
||||||||||||||||||||||||||||
модулирующей функции t |
M , |
определённой на конечном интервале значений t , |
|||||||||||||||||||||||||||||||||
соответствует определённое число - дискретное значение параметра ak . Функциональная |
|||||||
зависимость между действительными значениями t |
и ak |
здесь проявляется только в |
|||||
тех случаях, когда |
на тактовом интервале |
ˆ |
ˆ |
модулирующая |
функция |
||
t tk , tk 1 |
|||||||
постоянна: t k |
const . В таком случае |
имеем |
ak f k |
|
ˆ ˆ |
. Более |
|
|
|||||||
|
t tk , tk 1 |
||||||
того, предполагая, что модулирующая координата t постоянна на |
|
тактовом интервале, |
|||||
можно получить так называемую статическую характеристику ИЭ. Для этого необходимо знать среднее значение импульса, определяемое формулой
|
|
|
|
|
|
|
|
ˆ |
|
|
|
1 |
|
|
|
tk 1 |
|
uср |
|
|
|
|
|
u t dt . |
||
|
|
|
|
|
||||
ˆ |
|
|
ˆ |
|
||||
|
t |
k 1 |
t |
k |
ˆ |
|||
|
|
|
|
tk |
||||
Здесь u t |
- |
|
координата на выходе ИЭ. Зависимость uср - и есть статическая |
|||||
характеристика ИЭ, в частности, ИЭ, осуществляющего модуляцию второго рода.
Тактность модуляции связана с характером формирование импульсной последовательности, с полярностью формируемых импульсов. При однотактной модуляции двухполярному входному воздействию соответствует на выходе ИЭ однополярная последовательность импульсов, а при двухтактной модуляции - двухполярная последовательность импульсов.
Говоря о форме модулированных импульсов, необходимо отметить, что наибольшее распространение получили прямоугольная, треугольная, трапецеидальная и синусоидальная формы. При этом последовательность импульсов обычно характеризуется какой-то одной из них. Немаловажно, что изменение формы импульса часто рассматривается как способ улучшения результатов регулирования.
Тема 5.2. Использование микропроцессоров и микро-ЭВМ в системах управления
САУ, содержащую микро-ЭВМ в контуре, называют микропроцессорной автоматической системой (МП-системой), так как основой микро-ЭВМ является микропроцессор. Микро-ЭВМ в составе МП-системы выполняет роль управляющей ЭВМ. На рис. 1 показана типовая система управления такого рода. Если входным сигналом является цифровой код, то она состоит из цифровой ЭВМ, цифроаналогового преобразователя (ЦАП), управляемого объекта(процесса), аналогово-цифрового преобразователя (АЦП).
Рис. 1 - Функциональная схема типовой МП-системы с цифровым входом
ЭВМ преобразует входной сигнал в цифровой управляющий в соответствии с алгоритмом, заложенным в программу; АЦП, или квантователь, преобразует выходной сигнал управляемого процесса в последовательные импульсы; ЦАП, или экстраполятор, преобразует цифровой выход ЭВМ в аналоговый сигнал, который воздействует на управляемый процесс.
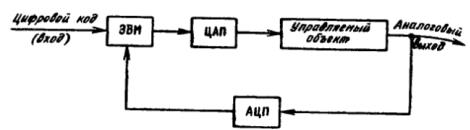
Если аналоговый вход и аналоговый выход (а не вход в виде цифрового кода), то используется схем, показанная на рис. 2.
Рис. 2 - Функциональная схема МП-системы с аналоговым входом
В технике ЭВМ используют в двух основных случаях.
1.ЭВМ применяют для моделирования и расчета динамики систем. Математические модели реальных систем описывают нелинейными уравнениями высокого порядка, что существенно затрудняет использование аналитических методов. Поэтому удобно проводит анализ и синтез сложных систем управления на ЭВМ. К моделированию на ЭВМ обращаются также для проверки результатов, полученных аналитическими методами.
2.ЭВМ используют в системах управления в качестве встроенных контроллеров или процессоров (микроконтроллеров и микропроцессоров соответственно). Для инженеров - специалистов по системам управления микроконтроллер представляет собой устройство, предназначенное для преобразования входного сигнала в выходной согласно некоторому алгоритму управления и программе, легко составляемой на языке высокого уровня. Так как управляемые процессы имеют в основном аналоговый характер, то в большинстве цифровых САУ циркулируют как аналоговые, так и цифровые сигналы. Следовательно, необходимо такое преобразование сигналов, которое обеспечивало бы взаимодействие цифровых и аналоговых элементов. Например, аналоговые сигналы должны быть подвергнуты аналогово-цифровому преобразованию перед дальнейшей их обработкой в цифровом процессоре или контроллере.
Аналогово-цифровое преобразование может быть записано как операция кодирования. В то же время цифровой код ЭВМ может быть послан на непрерывные устройства системы только после цифроаналогового преобразования.
Преимущества дискретных (цифровых) систем в современной технике управления и обработки информации следующее:
а) повышенная чувствительность, высокая надежность, отсутствие дрейфа, высокая помехоустойчивость, небольшие габариты и масса, низкая стоимость, удобство при программировании; б) высокая гибкость по сравнению с аналоговыми регуляторами, заключающаяся в изменении программы цифрового регулятора (в соответствии с требованиями разработчика) или адаптации к характеристикам объекта без каких-либо изменений в аппаратных средствах; в) возможность работы в режиме разделения времени и др.
Однако цифровым системам управления, и в особенности микропрцессорным, присущи следующие ограничения: а) частоты квантования сигналов по времени, снижает скорость выполнения программы вычисления в системе; б) разрядной сетки или числа бит в разрядовом слове управляющей ЭВМ.
При проектировании микро-ЭВМ следует предусмотреть все задачи, необходимые для логики ее функционирования; кроме того, требуется спроектировать модули памяти, а также соответствующий интерфейс для обмена информацией между ЭВМ и измерительными, усилительно-преобразующими устройствами системы.
Рассмотрим некоторые примеры цифровых систем управления техническими объектами.
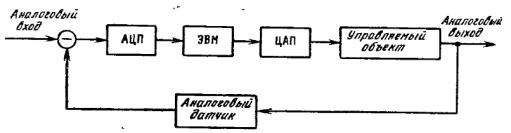
На рис. 3, а представлена функциональная схема аналоговой системы управления угловым движением самолета для одной управляемой переменной (угол тангажа, рыскания или крена). Цель управления состоит в отслеживании угла ориентации объекта за командным сигналом. Для улучшения устойчивости системы введена обратная связь по угловой скорости объекта.
Аналоговый автопилот (управляющая подсистема) может быть заменен на цифровой; при этом в систему должны быть включены аналогово-цифровой и цифроаналоговый преобразователи. Заметим, что поскольку все остальные элементы системы, кроме цифрового контроллера, остались аналоговыми, использование этих преобразователей является обязательным (рис. 3, б).
Рис. 3 - Функциональная схема САУ угловым движением самолета: а - с аналоговым автопилотом; б - с цифровым
Управление рядом производственных процессов осуществляют на основе применения ЭВМ (например, в современном прокатном производстве). На рис. 4 показана функциональная схема управления прокатным станом.
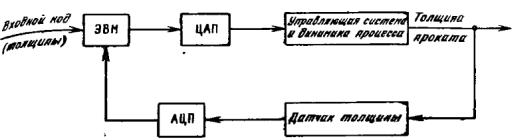
Рис. 4 - Функциональная схема системы управления прокатным станом
Непосредственной функцией цифровых ЭВМ является реализация управляющих алгоритмов, сформулированных разработчиком или пользователем, а задачей их периферии - сбор и регистрация исходных данных (значений параметров управляемого процесса), а также их обработка.
Существуют следующие режимы работы управляющей ЭВМ: диалоговый, пакетной обработки и реального времени. Расчеты экономического и научнотехнического характера выполняют в основном в диалоговом и пакетном режимах, когда время выполнения расчетов не оказывает влияния на конечный результат. Систему обработки данных в режиме реального времени можно определить как систему, получающую исходные данные и выдающую результат с такой скоростью, которая обеспечивает своевременную реакцию системы а изменения, происходящие во внешней
среде. Время |
ответа Ta управляющей ЭВМ должно соответствовать времени |
|||||
регулирования Tp процесса: |
||||||
T |
|
|
|
|
1 |
, |
p |
ср |
|
||||
|
|
|
2 fср |
|||
|
|
|
|
|||
где fср - частота среза системы, Гц.
Раздел 6. Линейные модели дискретных систем управления Тема 6.1. Решетчатые функции и разностные уравнения
Дискретность (и, следовательно, разрывность) сигналов обусловлена их квантованием по времени и (или) по уровню.
Дискретные сигналы могут принимать лишь дискретные значения в дискретные моменты времени.
В дальнейшем будем рассматривать сигналы, дискретные только по времени (только во временной области). Они представляют собой последовательность импульсов, появляющихся в определенные моменты времени.
На рис. 1 иллюстрируется принцип получения последовательности импульсов, основанный на пропускании непрерывного сигнала x t через ключ, который периодически, с тактом квантования T0 , замыкается на время h .
