UP_Vved_v_ekonometriku_-_N_Novgorod_2010

Величины ei признаются случайными, если выполняются следующие

Здесь квадратные скобки означают целую часть.

Если хотя бы одно из неравенств нарушается, то гипотеза о случайном характере отклонений отвергается.

II. Проверка равенства математического ожидания случайной

Это условие выполнимо для линейных моделей и нелинейных относительно факторных переменных, которые заменой переменных можно привести к линейному виду. Для моделей, нелинейных по оцениваемым параметрам и приводимых к линейному виду логарифмированием, средняя ошибка равна нулю для логарифмов исходных данных.

В тоже время из условия (5.7) не обязательно должно следовать условие равенства нулю математического ожидания величин i ,i 1,n ). Поэтому необходима проверка выполнимости этого условия.

На уровне значимости гипотеза отклоняется, если t расч t ,n 1 ..

III. Проверка независимости (отсутствия автокорреляции) в ряду остатков.

Корреляционная зависимость между рядом наблюдений и тем же рядом, сдвинутым на несколько шагов по времени, называется автокорреляцией.

Длину временного смещения называют лагом. Так как большое распространение имеют модели с лагом, равным одному году, то в некоторых работах автокорреляция определяется как корреляционная зависимость между соседними значениями уровней временного ряда.

Автокорреляция в остатках является нарушением условий ГауссаМаркова о независимости остатков. В этом случае cov(i , j ) 0, i, j 1,n , что

затрудняет применение классических методов анализа временных рядов, снижает эффективность применения МНК. Поэтому выработаны и применяются специальные статистические приемы для ее выявления

(критерий Дарбина — Уотсона, тест серий, тест Лююинга-Бокса и др)12 ,

смягчения и устранения.

12 Кремер Н.Ш.,Путко Б.А. Эконометрика. М.- Юнити, 2003, с.170

51

Критерий Дарбина-Уотсона (d-критерий).

Это наиболее распространенный и простой критерий (тест), выявляющий определяющий только автокорреляцию первого порядка, т.е. между рядами, сдвинутыми на одно значение (лаг=1). Он основан на простой идее: если имеется корреляция ошибок i , то она присутствует и в остатках ei ,

получающихся после применения МНК.

выборочный парный коэффициент корреляции между соседними уровнями ряда. Если автокорреляция отсутствует, то =0, следовательно, d 2 . В случае функциональной зависимости =1, а d 0 . Таким образом, интервал изменения d : 0 d 4 .

Близость статистики d к 4 свидетельствует об отрицательной автокорреляции остатков. Такая закономерность поведения последовательных может встретиться при работе, например с полугодовыми данными показателей с сезонным характером изменений. Близость d к нулю означает наличие положительной автокорреляции.4

Имеются таблицы критических точек распределения Дарбина – Уотсона (таблица 15). По ней для заданного уровня статистической значимости , числа наблюдений n и количества факторных переменных определяются два

1

автокорреляция.

На практике иногда пользуются следующим правилом: если расчетное значение статистики попадает в интервал (1,5–2,5), то считают, что автокорреляция отсутствует. При использовании данного критерия необходимо учитывать следующие ограничения:

d -критерий применим только для моделей со свободным членом;

d -критерий выявляет только автокорреляцию первого порядка

d -критерий не применим для моделей, включающих в качестве факторной переменной зависимую переменную с одним лагом (т.е. для авторегрессионных моделей).

52

Тест Бреуша-Годфри

Тест основан на следующей идее: если имеется корреляция между соседними наблюдениями, то естественно ожидать, что в уравнении

коэффициент окажется значимо отличающимся от нуля.

При практическом выполнении теста оцениваем параметры (5.9) по МНК и проверяем статистическую значимость .

Нетрудно показать, что в случае гомоскедастичности дисперсий , параметр совпадает с парным коэффициентом корреляции между t и

Этот тест может быть обобщен на случай включения в уравнение (5.9) остатков с лагами 2, 3 и т.д., что позволяет выявить корреляцию не только между соседними уровнями, но и более отдаленными

IV. Проверка ряда остатков на нормальность распределения.

Для проверки статистической значимости параметров и прогнозирования по трендовой модели, ряд остатков должен подчиняться нормальному закону распределения. Существует целый ряд тестов и критериев проверки выполнимости данного предположения (с помощью исследования показателей асимметрии и эксцесса; метода Вестергарда, RS–критерия и пр.).

RS–критерий.

Имеются теоретические таблицы критических значений величины RS., рассчитанные для различных доверительных вероятностей в зависимости от

числа переменных n.(таблица 16) Если расчетное значение RS попадает между табулированными значениями a и b , т. е. a RS b при выбранном уровне доверия, то принимается гипотеза о соответствии ряда остатков нормальному закону распределения, в противном случае эта гипотеза отвергается.

5.6. Прогнозирование на основе трендовой модели

Прогнозирование на основе трендовых моделей основано на идее экстраполяции, т.е. предполагаем, что закономерности, связи, относящиеся к прошлому сохраняться в будущем. По трендовой модели строится упреждающий точечный и интервальный прогноз. Так, если длина временного ряда n , то для прогнозирования выбирается t n 1 или t n 2.

Прогнозировать на большее число шагов не рекомендуется из-за увеличивающейся расплывчатости прогноза.

53

маловероятно. Поэтому точечный прогноз должен сопровождаться интервальным прогнозом. Рассмотрим случай линейного тренда.

Для нахождения интервального прогноза строим доверительный интервал для условного среднего значения изучаемого показателя в точке t n 1 :

неопределенности прогнозируемого процесса с ростом периода упреждения проявляется в постоянном расширении доверительного интервала. Результаты прогноза должны быть проанализированы с содержательной точки зрения.

54

6. Примеры построения эконометрических моделей.

6.1. Модель парной регрессии

Пример. Построить эконометрическую модель зависимости объема выпуска продукции Y от изменений затрат основных фондов X. Статистические данные приведены в следующей таблице

1.Построение модели

Предположим, что между исследуемыми показателями существует линейная зависимость: Y X . Оценим параметры этой модели на основе метода наименьших квадратов. Уравнение оцененной модели:

ˆ

Y a b X

Таблица 7.

Таблица для расчета параметров и характеристик модели.

Запишем систему нормальных уравнений и найдем ее решение.

a 15 b 20

15 a 297,67 b 355,78

a 20 0,7676 15 8,486

Получили следующее уравнение модели: Y 8,486+0,7676 X.

2. Проверка качества уравнения регрессионной модели

а). Проверка статистической значимости параметров модели.

Так как модель построена на основе выборочных данных, необходима

55

между объемом выпуска и затратами основных фондов. Построим доверительный интервал для параметра b :

Значение R2 свидетельствует о сильной связи между Y и X и при условии статистической значимости коэффициента корреляции R обеспечивает

значимым, а так как он характеризует сильную связь факторной переменной X и результативного показателя Y , модель можно считать адекватной.

в). Точность модели

Точность модели определяется на основе средней относительной ошибки

56

Так как средняя относительная ошибка аппроксимации менее 10%, точность модели признается хорошей.

Проведенный анализ качества модели свидетельствует о том, что построена адекватная, надежная и точная модель.

3.Прогнозирование на основе построенной модели

Выберем для исследования значение основных фондов X=20. Для нахождения точечного прогноза подставим X=20 в уравнение модели

Y(20)=8,49+0,77 20=23,89;

Найдем интервал разброса средних значений объема выпуска при выбранном объеме основных средств X=20.

Для этого сначала рассчитаем выборочную дисперсию Y в точке X=20.

Построим доверительный интервал (уровень доверия 95%) для среднего значения Y при X0=20:

23,89 2,365 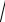0,11 M (YX ( X0 20) 23,89 2,365 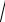0,11

Следовательно, ожидаемое значение объема выпуска при затратах основных фондов в 20 единиц с вероятностью 95% будет находиться в интервале: 23,1 M (YX ( X0 20)) 24,67

6.2. Модель множественной регрессии

Пример. Имеются статистические данные о приращении прибыли (Y) по 7 предприятиям отрасли в зависимости от инвестиционных вложений в оборотные средства ( X1) и основной капитал ( X 2 ). Проанализировать

зависимость приращения прибыли от этих показателей. Исходные данные приведены в таблице

1. Построение модели

Рассмотрим двухфакторную линейную модель:

Y 0 1 X1 2 X 2 . Оценим ее параметры на основе МНК.

Система нормальных уравнений для модели множественной регрессии:

57

1470 X T Y 215940

25150

Запишем систему нормальных уравнений:

Уравнение модели: Y 61,36 0, 25 X1 16,07 X2 .

2. Проверка качества модели.

Сформируем вспомогательную таблицу (табл. 8) для расчета характеристик модели.

a). Проверка общего качества модели.

58

Оба коэффициента детерминации свидетельствуют о сильной связи между факторными переменными и результативным показателем.

Табличное значение статистики Fтабл ( =0,05;2,4))=6,94.(таблица 13) Так как расчетное значение статистики F много больше критического значения F, то модель признается адекватной и надежной с вероятностью. 95%.

b). Проверка статистической значимости параметров модели.

Найдем стандартные ошибки в вычислении параметров модели:

Для проверки значимости параметров найдем статистики Стьюдента:

Теоретическое значение статистики Стьюдента t(n m 1 4; 0,05) 2,776 .

Для коэффициента a1 расчетное значение статистики меньше теоретического, поэтому нельзя отвергнуть гипотезу о его равенстве нулю и признать его статистически значимым. Коэффициент a2 является статистически значимым,

так как ta2 t (4;0,05)

в). Точность модели

Для характеристики точности рассчитывается средняя относительная

59

не превосходит 10%, поэтому можно считать точность модели хорошей.

3. Анализ влияния факторных переменных на результативный

показатель.

1. Рассчитаем коэффициенты эластичности :

Это означает, что при увеличении вложений в оборотный капитал на 1% (фактор X1 ) и неизменной величине вложений в основной капитал прибыль

предприятий возрастет на 0,14%. При увеличении вложений в основной капитал (фактор X 2 ) на 1% прибыль возрастет на 1,15%, те инвестиционные

вложения в основной капитал более значимы для предприятий.

Рассчитаем – коэффициенты. Для этого найдем среднеквадратичные отклонения для факторных переменных и результативного показателя.