
Vmfmm_StatGip_308_2011
.pdf
ФГБОУ ВПО «Воронежский государственный технический университет»
Кафедра высшей математики и физико-математического моделирования
308 - 2011
ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ для организации самостоятельной работы
по курсу "Высшая математика" для студентов специальностей 280103 "Защитавчрезвычайныхситуациях",
280101 "Безопасностьжизнедеятельностивтехносфере" и направления 280200 "Защитаокружающейсреды"
очной формы обучения
Воронеж 2011
Составители: канд. физ.-мат. наук И.Н. Пантелеев аспирант А.И. Пантелеев
УДК 51 (075)
Проверка статистических гипотез: методические указания для организации самостоятельной работы по курсу "Высшая математика" для студентов специальностей 280103 "Защита в чрезвычайных ситуациях", 280101 "Безопасность жизнедеятельности в техносфере" и направления 280200 "Защита окружающей среды" очной формы обучения / ФГБОУ ВПО «Воронежский государственный технический университет»; сост. И.Н. Пантелеев, А.И. Пантелеев. Воронеж, 2011. 54 с.
Методические указания предназначены в качестве руководства для организации самостоятельной работы по курсу "Высшая математика" по разделу «Теория вероятностей и матстатистика» для студентов специальностей 280103 (ЧС), 280101 (БЖ) и направления 280200 (ЗС) в 4 семестре. В работе приведен теоретический материал, необходимый для выполнения заданий и решения типовых примеров.
Методические указания подготовлены на магнитном носителе в текстовом редакторе Microsoft Word 2003 и
содержатся в файле Vmfmm_StatGip.pdf.
Табл 9. Ил. 2. Библиогр.: 8 назв.
Рецензент канд. физ.-мат. наук, доц. В.В. Ломакин Ответственный за выпуск зав. кафедрой д-р физ.-мат. наук, проф. И.Л. Батаронов
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
© ФГБОУ ВПО «Воронежский государственный технический университет», 2011
1. Элементы теории корреляции
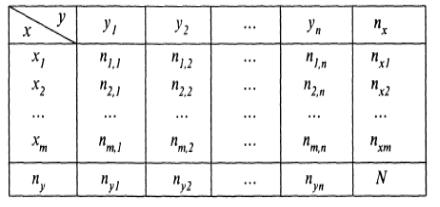
1°. в массовых явлениях некоторому значению одной величины x соответствует распределение значений другой у, причем с различными вероятностями.
Связь такого характера называется статистической и, как правило, задается таблицей распределения или корреляционной таблицей, связывающей значения переменных.
Во внутренних клетках таблицы обозначены частоты
появления |
переменной xi (i =1,..., m), |
соответствующей |
переменной |
yi (i =1,..., n). Суммы чисел |
ni, j по строкам |
представляют частоты соответствующих значений переменной xi . Так
∑n1, j = n1,1 +n1,2 +...+n1,n = nx1
∑n2, j = n2,1 +n2,2 +... +n2,n = nx2 ,...
Суммы чисел по столбцам представляют частоты соответствующих значений переменной
∑ni,1 = n1,1 +n2,1 +... +nm,1 = ny1
∑ni,2 = n1,2 +n2,2 +... +nm,2 = ny2 ,...
причем ∑nx = ∑ny = N.
Математическая обработка корреляционной таблицы позволяет установить форму корреляционной связи между переменными x и y и тесноту этой связи. Найденные из этой таблицы пары соответствующих значений yx и x (у по x) или
xy и y (x по у) используются для отыскания параметров
уравнений регрессии.
Методы математического описания анализа корреляционных (стохастических) связей между признаками рассматриваются в разделах корреляционного и регрессионного анализа математической статистики.
Уравнение M x (Y )= f (x), описывающее зависимость
условного математического ожидания случайной величины Y при заданном X - x, называется уравнением регрессии Y на X, а график этого уравнения на плоскости будет линией регрессии. Корреляционная связь между X и Y характеризуется двумя параметрами: формой связи и теснотой этой связи. Форма корреляционной связи определяется формой линии регрессии.
Различают положительную и отрицательную, линейную и нелинейную корреляцию. Теснота связи характеризуется степенью случайного разброса величин признака У вокруг линии регрессии, чем меньше разброс, тем связь будет теснее.
2°. В случае линейной корреляции уравнения прямых регрессии имеют вид
yx = ax +b и xy = cy +d. |
(1) |
Система нормальных уравнений для отыскания параметров а и b уравнения прямой регрессии у по х, получаемая в результате использования метода наименьших квадратов, имеет вид
a∑nx x2 +b∑nx x = ∑nx xyx , |
(2) |
a∑nx x +b∑nx = ∑nx yx , |
|
а для отыскания параметров с и d уравнения прямой регреcии x по у
2

c∑ny y2 +d ∑ny y = ∑ny yxy , |
(3) |
c∑ny y +d ∑ny = ∑ny xy . |
|
3°. Схема расчета. Расчет удобнее вести в табличном виде:
1 |
2 |
3 |
4 |
5 |
6 |
7 |
xi |
nx |
nx x |
nx x2 |
yx |
nx yx |
nx xyx |
… |
… |
… |
… |
… |
… |
… |
∑ |
N |
∑nx x |
∑nx x2 |
∑yx |
∑nx yx |
∑nx xyx |
а) для каждого значения xi находим сумму частот и
располагаем их во втором столбце; б) третий столбец равен произведению членов первых двух
столбцов, а четвертый равен произведению членов второго на квадраты первого, соответственно;
в) в пятом столбце для каждого значения xi корреляционной таблицы находим среднее значение yx по правилу определения средней взвешенной
|
|
yx = |
∑nxi yxi |
, |
|
|
|
nx |
|
||
|
|
|
|
|
|
где |
nx — частота |
появления |
значения |
xi , yx — |
|
|
|
|
|
|
i |
соответствующее значению |
xi при данной частоте значение |
||||
переменной y. |
|
|
|
|
|
|
г) шестой столбец равен произведению членов второго и |
||||
пятого, а седьмой третьего и пятого. |
|
|
|||
|
Поскольку |
|
|
|
|
|
∑nx x = Nx, ∑nx x2 |
= Nx 2 , ∑nx yx = Ny, |
(4) |
||
∑nx xyx = Nxy,
3
то после сокращения на N система (2) примет вид ax 2 +bx = xy,
ax +b = y.
Откуда уравнение прямой регрессии у по x имеет вид yx − y = ρy / x (x − x ),
(5)
(6)
здесь ρ |
y / x |
= xy − x y |
|
- |
коэффициент прямой регрессии у |
||||||||||||||||||||||
по x. |
|
|
x 2 − x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналогично, уравнение прямой регрессии x по у |
|
||||||||||||||||||||||||||
|
|
|
|
|
xy − x = ρx / y (y − y ), |
|
|
|
|
|
|
(7) |
|||||||||||||||
где ρ |
y / x |
= xy − x y |
|
- коэффициент прямой регрессии х по y |
|||||||||||||||||||||||
|
|
y 2 − y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
y = |
∑ny y |
; |
y |
2 |
= |
∑ny y2 |
; |
|
x = |
|
∑ny xy |
; |
|
||||||||||||
|
|
|
N |
|
|
|
N |
|
|
|
N |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
xy = |
∑ny yxy |
; |
N = |
∑ny . |
|
(8) |
||||||||||||||
|
|
|
|
|
|
|
|
|
N |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Если ввести коэффициент корреляции, характеризующий |
|||||||||||||||||||||||||||
меру тесноты линейной корреляционной связи |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
r = xy − xy , |
|
|
( |
|
r |
|
<1 |
|
|
|
(9) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
σxσy |
|
|
|
|
|
|
|
|
) |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
то коэффициенты регрессии примут вид |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
ρ |
y |
/ x |
= r |
|
σy |
; |
ρ |
y / x |
|
= r |
σx |
, |
|
(10) |
||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
σ |
x |
|
|
|
|
|
|
σ |
y |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4

где σx2 = x 2 − x 2 , σy2 = y2 − y 2 — дисперсии соответствующих
рядов распределений. Если r < 0,4, то считают, что линейной корреляции между x и у нет. Чем |r| ближе к единице, тем теснее связь между переменными.
3°. Упрощенный способ вычисления коэффициента корреляции. При постоянных разностях x и y в таблице
распределения вычисления значительно упрощаются, если перейти к новым переменным
u = |
x − x0 |
, |
υ = |
y − y 0 |
, |
(11) |
|
x |
y |
||||||
|
|
|
|
|
где x0 , y 0 — произвольно выбираемые значения переменных x
и у (обычно их средние или ближайшие к ним).
Вычисление коэффициентов корреляции и коэффициентов регрессии сводится к аналогичным операциям над новыми переменными u и υ (со значительно меньшими по абсолютной величине числами). Так
r = xy − xy |
= |
u |
υ |
− |
u |
υ |
, |
|
σ σ |
|
|
σ |
σ |
υ |
|
||
x y |
|
|
|
u |
|
|
||
ρ = xy − xy
y / x x 2 − x 2
ρx / y = xy − xy y 2 − y2
− = |
y |
u |
υ |
− |
u |
υ |
= |
y συ r, |
(12) |
|||
|
x |
u |
2 − |
u |
2 |
|
x σu |
|
||||
− = |
x |
u |
υ |
− |
u |
υ |
= |
x σu r. |
|
|||
|
y υ |
2 −υ |
2 |
|
y συ |
|
||||||
Новые переменные u, υ помещают в исходной таблице, соответственно, и—слева от соответствующих значений x, а υ
— над соответствующими значениями у.
Если линейная корреляция обнаруживает малую тесноту связи r = 0,4 ~ 0,6, то следует обратиться к криволинейной корреляции.
4°. Если корреляционная зависимость между значениями x и у корреляционной таблицы близка к параболической, то уравнение регрессии примет вид
5

yx = ax2 +bx +c, |
(13) |
где параметры а, b, с на основании метода наименьших квадратов определяются из решения системы нормальных уравнений
a∑nx x4 +b∑nx x3 +c∑nx x2 = ∑x2nx yx ,
a∑nx x3 +b∑nx x2 +c∑nx x = ∑xnx yx , (14) a∑nx x2 +b∑nx x +cN = ∑ nx yx .
5°. В случае корреляционной |
зависимости гиперболи- |
|||||||
ческого типа уравнение регрессии имеет вид |
||||||||
|
|
yx = a + b , |
|
|
(15) |
|||
|
|
|
|
x |
|
|
|
|
где параметры а, b определяются из решения системы |
||||||||
нормальных уравнений |
= aN +b∑nx 1 |
|
|
|||||
∑nx yx |
, |
|
||||||
|
|
|
|
|
x |
(16) |
||
∑nx |
yx |
= a∑ |
nx |
+b∑ |
nx |
|
||
x |
|
2 |
||||||
|
|
x |
|
|
x |
|||
При составлении системы нормальных уравнений (14), (16) необходимые данные целесообразно вычислять в табличном виде.
1.1. Дана корреляционнаф таблица.
y |
11 |
21 |
31 |
41 |
51 |
nx |
x |
|
|
|
|
|
|
15 |
2 |
3 |
- |
- |
- |
5 |
20 |
- |
4 |
6 |
- |
- |
10 |
25 |
- |
4 |
10 |
3 |
- |
17 |
|
- |
2 |
16 |
10 |
- |
28 |
30 |
- |
- |
8 |
12 |
5 |
25 |
35 |
- |
- |
- |
8 |
7 |
15 |
40 |
|
|
|
|
|
|
ny |
2 |
13 |
40 |
33 |
12 |
100 |
6

Найти уравнение прямой регрессии: а) y по x ; б) x по у. Решение. а) Проведем расчет в табличном виде
xi |
|
nx |
nx x |
|
nx x2 |
yx |
|
|
|
|
nx yx |
|
|
|
nx x yx |
||||||
15 |
|
5 |
|
75 |
|
|
|
1125 |
17 |
|
|
|
85 |
|
|
|
1275 |
||||
20 |
|
10 |
200 |
|
|
4000 |
27 |
|
|
|
270 |
|
|
|
5400 |
||||||
25 |
|
17 |
425 |
|
|
10625 |
30,41 |
|
|
516,97 |
|
|
12924,25 |
||||||||
30 |
|
28 |
840 |
|
|
25200 |
33,86 |
|
|
948,08 |
|
|
28442,4 |
||||||||
35 |
|
25 |
875 |
|
|
30625 |
39,8 |
|
|
|
995 |
|
|
|
34825 |
||||||
40 |
|
15 |
600 |
|
|
24000 |
45,66 |
|
|
684,9 |
|
|
|
27396 |
|||||||
∑ |
|
100 |
3015 |
|
95575 |
193,74 |
|
3499,95 |
|
|
110262,65 |
||||||||||
|
|
По данным таблицы и формулам (4) |
x |
= |
∑nx x |
=30,15; |
|||||||||||||||
|
|
100 |
|
||||||||||||||||||
|
|
|
|
|
|
∑nx yx |
|
|
|
|
|
|
|
|
|
|
|
||||
x |
2 |
=909,0225; |
y = |
=34,999; x |
2 |
= |
∑nx x2 |
=955,75; |
|||||||||||||
|
|
100 |
|
|
100 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x y =1055, 23; |
xy = |
∑nx xyx |
=1102,63. |
|
|
|
|
|
|
|
|
||||||||||
|
100 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Коэффициент регрессии y по x равен |
|
|
|
|
|
|
|
||||||||||||
|
|
ρy / x = |
1102,63 −1055, 23 |
=1,014. |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
955,75 −909,0225 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Таким образом, уравнение прямой регрессии у по x (6) |
|||||||||||||||||||
примет |
вид |
|
|
yx −34,999 =1, 014(x −30,15) |
или |
||||||||||||||||
yx =1,014 +4, 4269.
б) При определении прямой регрессии x по y составим вспомогательную таблицу
y |
n |
y |
n |
y |
y |
n |
y |
y2 |
x |
y |
n |
y |
x |
y |
n |
y |
yx |
y |
i |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
30 |
|
|
|
|
|||||||
11 |
2 |
|
22 |
|
242 |
15 |
|
|
330 |
|
||||||||
21 |
13 |
273 |
5733 |
21,923 |
284,999 |
5984,98 |
||||||||||||
31 |
40 |
1240 |
38440 |
28,25 |
1130 |
37510 |
||||||||||||
41 |
33 |
1353 |
55473 |
33,788 |
1115,004 |
45715,164 |
||||||||||||
51 |
12 |
612 |
31212 |
30,333 |
363,9996 |
18563,979 |
||||||||||||
∑ |
100 |
3500 |
131100 |
131,29 |
3004,0026 |
108104,12 |
||||||||||||
7
По данным таблицы и формулам (8) x = ∑100ny xy =30,04;
y = |
∑ny y |
=35; y |
2 |
=1225; |
y |
2 |
= |
∑ny y2 |
=1311; |
100 |
|
|
100 |
||||||
|
|
|
∑ny yxy |
|
|
|
|
||
x y =1051, 4; xy = |
=1081,0412. |
|
|||||||
100 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
Коэффициент регрессии x по y равен
ρ =1081,04 −1051, 4 =
x / y 0,34465. 1311−1225
Уравнение прямой регрессии x по y (7) примет вид
xy −30,04 = 0,34465(y −35), xy = 0,34465y +17,97725.
1.2. Пользуясь таблицей распределения задачи 1.1, найти упрощенным способом коэффициент корреляции и уравнения прямых регрессий.
Решение. Дополним заданную корреляционную таблицу соответствующими значениями u и υ , полагая, что x0 = 30,
y0 = 31.
|
υ |
|
-2 |
-1 |
0 |
1 |
2 |
|
u |
x |
y |
11 |
21 |
31 |
41 |
51 |
nx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-3 |
15 |
|
2 |
3 |
- |
- |
- |
5 |
-2 |
20 |
|
- |
4 |
6 |
- |
- |
10 |
-1 |
25 |
|
- |
4 |
10 |
3 |
- |
17 |
0 |
30 |
|
- |
2 |
16 |
10 |
- |
28 |
1 |
35 |
|
- |
- |
8 |
12 |
5 |
25 |
2 |
40 |
|
- |
- |
- |
8 |
7 |
15 |
|
ny |
|
2 |
13 |
40 |
33 |
12 |
100 |
|
|
|
|
|
|
|
|
|
8
Составляем вспомогательные таблицы
u |
nx |
nxu |
nxu2 |
nxυu |
|
unxυu |
|
-3 |
5 |
|
-15 |
45 |
-7 |
|
21 |
-2 |
10 |
|
-20 |
45 |
-4 |
|
8 |
-1 |
17 |
|
-17 |
17 |
-1 |
|
1 |
0 |
28 |
|
0 |
0 |
8 |
|
0 |
1 |
25 |
|
25 |
25 |
22 |
|
22 |
2 |
15 |
|
30 |
120 |
22 |
|
44 |
∑ |
100 |
|
3 |
247 |
40 |
|
96 |
υ |
|
ny |
|
nyυ |
|
nyυ2 |
|
|
|
|
|
|
|
|
|
-2 |
|
2 |
|
-4 |
|
8 |
|
-1 |
|
13 |
|
-13 |
|
13 |
|
0 |
|
40 |
|
0 |
|
0 |
|
1 |
|
33 |
|
33 |
|
33 |
|
2 |
|
12 |
|
24 |
|
48 |
|
∑ |
|
100 |
|
40 |
|
102 |
|
По данным расчетов находим: N = 100;
|
|
|
|
|
∑nxu |
|
|
|
|
|
|
|
|
|
∑nyυ |
|
|
|
|
|
2 |
|
∑nxu2 |
|
||||||
u = |
= |
0,03; υ = |
= 0,04; |
u |
= |
= 2, 47; |
||||||||||||||||||||||||
|
N |
|
N |
|
|
|
N |
|||||||||||||||||||||||
|
|
2 |
|
|
∑nyυ2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||
υ |
= |
=1,02; |
u |
|
= 0,0009; υ |
= 0,16; |
|
|||||||||||||||||||||||
|
|
N |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
∑unxυu |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
uυ |
= |
= 0,96. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x =5, |
|
y =10 и средние значения новых |
||||||||||||||||
|
|
|
|
|
Учитывая, что |
|
||||||||||||||||||||||||
переменных |
u |
= 0,03,υ |
= 0, 4, находим средние значения |
|||||||||||||||||||||||||||
старых переменных |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x = x0 + |
u |
|
x =30 +0,03 5 = 30,15; |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y = y0 +υ |
y = 31+0, 4 10 = 35. |
|
|||||||||||||||||
9
