UP_Vved_v_ekonometriku_-_N_Novgorod_2010

то нулевая гипотеза отвергается и уравнение признается статистически значимым. .

Качество подбора функции можно оценить сравнением двух оценочных дисперсий: дисперсии остатков и общей дисперсии. Если Se2 > S 2 , то

исследуемое уравнение определяет не адекватную модель и ее нужно отвергнуть.

F–статистика может быть выражена через коэффициент детерминации:

Поделим последнее соотношение на TSS и получим

статистической проверки гипотез с использованием t – статистики Стьюдента. Расчетное значение статистики:

статистически значимым, а модель адекватной и надежной. Для коэффициента корреляции может быть построен доверительный интервал:

R tтабл SR M (R) R tтабл SR

Чем шире интервал, тем больше неопределенность в оценке связи Y и X .

величина в каждом наблюдении представляет собой абсолютную ошибку аппроксимации. Но эти величины несравнимы между собой, так как зависят от единиц измерения и масштаба величин Yi . Так, если в одном наблюдении

получилась ошибка 5, а в другом 10, это не означает, что в последнем случае модель дает худший результат.

Поэтому для того, чтобы оценки были сравнимыми, рассматривают относительные оценки i (отношения отклонений ei к фактическим значениям

31

Yi (в процентах)). Поскольку отклонения ei могут быть как положительными, так и отрицательными, то отклонения берутся по модулю.

аппроксимации в i–м наблюдении. Чтобы иметь общее суждение о точности модели, определяют среднюю относительную ошибку аппроксимации:

Ошибка менее 7%-10% свидетельствует о хорошем подборе модели к исходным данным (хорошая точность). При ошибке более 12-15 % следует подумать о выборе другого типа уравнения модели. В эконометрическом анализе используют и другие алгоритмы для расчета точности модели.

4. Некоторые вопросы практического использования регрессионных моделей.

4.1. Применение эконометрических моделей для прогнозирования.

Одной из основных задач эконометрического моделирования является прогнозирование значений зависимой переменной при определенных значениях объясняющих переменных.

Параметры a и b содержат случайные ошибки. В результате зависимая

ˆ

переменная Y ( X 0 ) , найденная по уравнению модели в некоторой точке X 0 , является случайной величиной и, следовательно, определяет некоторое

условное среднее значение Y в точке X 0 (точечная оценка). Обозначим ее – YX 0 . Найдем дисперсию этой величины.

6 Джонсон « Эконометрические методы», М., Статистика. 1980, стр. 29

32

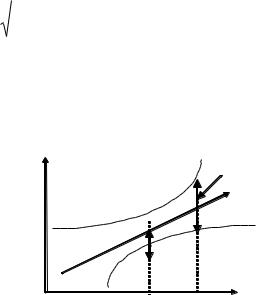
среднего значения ширина доверительного интервала увеличивается (рис. 5.2).

Y

Доверительный итервал

Рис. 5. Доверительная область для условных средних зависимой переменной.

Построенная на рисунке доверительная область определяет местоположение модельной линии регрессии, т.е. условного математического ожидания, но не отдельных возможных значений зависимой переменной, которые могут варьировать около средней.

Иногда нас больше может заинтересовать отыскание доверительного

интервала для некоторого индивидуального значения Y * , которое мы связываем с X 0* .

В несколько иной форме эта проблема может быть сформулирована так:

33

распределение, следовательно, величина t z имеет распределение Стьюдента

Sz

с (n 2) степенями свободы.

Если расчетное значение t–статистики будет больше табличного, то нулевая гипотеза отвергается, т. е. с выбранным уровнем доверия можно

утверждать, что значение Y * статистически значимо (существенно) отличается

т.е. для индивидуальных значений следует учитывать еще один источник

Очевидно, что этот интервал при том же уровне доверия шире, чем для

условного среднего YX 0 и включает в себя доверительный интервал для

условного среднего значения.

Обобщим полученные результаты на случай модели множественной регрессии.

Доверительные интервалы в этом случае строятся в предположении,

что факторные переменные приняли значения, задаваемые матрицей (вектором)

Доверительный интервал для условного среднего определяется, как и в случае парной регрессии, по формуле:

Аналогичный доверительный интервал для индивидуальных значений зависимой переменной примет вид:

7 Джонсон « Эконометрические методы», М., Статистика. 1980, стр. 49

34

Таким образом, процесс прогнозирования, опирающийся на эконометрическую модель распадается на следующие этапы:

выбор и построение модели;

оценка построенной модели;

прогноз (точечный и интервальный).

Для получения точечного прогноза подставляют исследуемое значение

X 0 в уравнение модели и находят Y ( X 0 ) . Это и есть точечный прогноз.

Однако, вероятность попадания Y в найденную точку Y ( X 0 ) практически

равна нулю, поэтому возникает необходимость перспективных оценок в виде "вилки" через доверительные интервалы – интервальный прогноз.

Исследуемое значение X 0 может лежать как внутри выборки, так и вне ее. В то же время, если X 0 выходит за пределы выборки и сильно отличается от среднего, ширина доверительного интервала существенно увеличивается, а

прогнозированием соответствующих временных рядов при условии, что исходные данные показателя представляют некоторый временной ряд, имеющий тенденцию и предполагается сохранение этой тенденции на перспективу. Полученные на основе прогноза данные должны быть критически осмысленны с содержательной точки зрения.

4.2. Экономическая интерпретация связи переменных в модели множественной регрессии

Для экономической интерпретации связей между факторными переменными и зависимой переменной обычно используют коэффициенты

эластичности, бета–коэффициенты и дельта–коэффициенты.

Коэффициенты эластичности характеризуют относительное изменение зависимой переменной при изменении объясняющей переменной на 1%. Если уравнение модели Y F( X ) , то коэффициент эластичности рассчитывается

следующим образом:

где X , Y – средние величины, а производная берется в точке X . Бета–коэффициенты ( – коэффициенты) или коэффициенты регрессии

в стандартизованном виде используются для устранения различий в измерении и степени колеблемости факторов.

35

среднеквадратичного отклонения изменится в среднем значение зависимой переменной при изменении факторного признака на величину его среднеквадратичного отклонения.

Дельта–коэффициент характеризует вклад каждого фактора в суммарное влияние на результирующий показатель (при условии независимости факторов).

регрессии имеют тот же знак, что и соответствующие парные коэффициенты корреляции. Тем не менее, в случае сильной коррелированности объясняющих переменных некоторые дельта–коэффициенты могут быть отрицательными вследствие того, что соответствующий коэффициент регрессии имеет знак, противоположный парному коэффициенту корреляции.

4.3. Проблемы спецификации модели.

Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели. Он включает в себя два круга вопросов: отбор факторов и выбор вида уравнения регрессии.

Включение в уравнение множественной регрессии того или иного набора факторов связано, прежде всего, с представлением исследователя о природе взаимосвязи моделируемого показателя с другими экономическими показателями. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям.

1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного

36

измерения, то ему нужно придать количественную определенность.

2. Факторы не должны иметь сильную корреляционную зависимость и тем более находиться в точной функциональной связи. Включение в модель таких факторов может привести к ненадежности оценок коэффициентов регрессии.

Однако теоретический анализ часто не позволяет однозначно ответить на вопрос о количественной взаимосвязи рассматриваемых показателей и их целесообразности включения в модель. Поэтому отбор факторов целесообразно разбить на два этапа:

на первом – подбираются факторы исходя из сущности проблемы, на основании допущений экономической теории.

на втором – отбор факторов осуществляется на основе методов многомерного статистического анализа.

При статистическом отборе факторных признаков можно рассмотреть два

альтернативных подхода: метод шаговой регрессии и метод

последовательного исключения факторных переменных Сущность метода шаговой регрессии заключается в последовательном

включении в уравнение отобранных на этапе содержательной постановки задачи факторных переменных с последующей проверкой качества модели и статистической значимости включенных переменных.

Оптимальный набор факторов можно было бы получить последовательным перебором всех возможных сочетаний факторных переменных, но этот путь чрезвычайно трудоемок и практически невозможен при большом числе переменных. Обычно рекомендуют следующую последовательность проведения шагового отбора переменных:

Сначала в модель включается переменная, имеющая наибольшую связь

срезультативным показателем (наибольший коэффициент парной корреляции). Строится модель регрессии. При условии надежности уравнения в целом

и статистической значимости включенной переменной добавляем следующую переменную и вновь проверяем качество модели и статистическую значимость.

Вдальнейшем эта переменная включается во все последующие уравнения.

На следующем шаге определяется наилучшая пара факторных переменных по условию максимума скорректированного коэффициента детерминации и статистической значимости включенных переменных.

Затем определяется наилучшая тройка факторов, причем в ней обязательно присутствуют переменные, включенные на предыдущих этапах и т.д.

Таим образом, при использовании шаговой регрессии обычно строится несколько альтернативных моделей.

Для выбора наилучшей из них обычно используют следующие критерии

детерминации.

Минимальная ошибка оценки точности модели.

Нормальность распределения остатков.

37

Независимость остатков (проверяется, например, с помощью критерия Дарбина – Уотсона).

Подтверждение выбора модели при помощи информационных критериев Акаике или Шварца

Критерии Акаике и Шварца являются эвристической попыткой свести в один показатель два требования: уменьшение числа параметров модели и улучшение качество подгонки модели:

Согласно этим критериям из двух моделей следует выбрать модель с наименьшим значением AIC (информационный критерий Акаике) или SC

(критерий Шварца)

где RSSm – остаточная сумма квадратов, полученная при оценивании

коэффициентов модели с m факторными переменными методом наименьших квадратов.

В обоих случаях при увеличении количества объясняющих переменных первое слагаемое в правой части уменьшается, а второе увеличивается. В критерии Шварца используется больший штраф за увеличение количества параметров модели.

Суть метода исключений состоит в следующем:

в уравнение включаются все переменные, выбранные на этапе содержательного анализа. Если значимыми оказываются не все параметры модели, то составляется новое уравнение, из которого исключается переменная, с наиболее незначимым параметром (меньшее значение t–статистики). Процедура повторяется до получения уравнения со всеми значимыми параметрами. В то же время этот вопрос об исключении той или иной переменной должен решаться с учетом содержательных аспектов проблемы и целей исследования.

4.4. Понятие мультиколлинеарности

При построении модели множественной регрессии часто приходится сталкиваться с явлением мультиколлинеарности.

Мультиколлинеарность – это коррелированность двух или нескольких объясняющих переменных в уравнении регрессии. В результате высококоррелированные объясняющие переменные действуют в одном направлении и имеют недостаточно независимое колебание, чтобы иметь возможность интерпретировать изолированное влияние каждой переменной.

Мультиколлинеарность особенно часто имеет место при анализе макроэкономических данных. Получаемые при этом оценки МНК чаще всего оказываются статистически незначимыми и ненадежным, хотя значения коэффициентов R2 могут быть высокими.

Для выявления мультиколлинеарности обычно рассчитывают матрицу парных коэффициентов корреляции для всех объясняющих переменных. Если коэффициенты корреляции между отдельными объясняющими переменными

38

достаточно велики (более 0,8–0,9), то, можно предположить, что они коллинеарны.

Более информативной является матрица частных коэффициентов корреляции, так как в ряде случаев парные коэффициенты корреляции могут давать совершенно неверные представлении о характере связи между двумя переменными. Например, между двумя переменными X и Y может быть высокий коэффициент парной корреляции не потому, что одна из них стимулирует изменение другой, а потому что обе эти переменные изменяются в одном направлении под влиянием других переменных. Поэтому появляется необходимость измерять действительную тесноту связи между двумя переменными, очищенную от влияния на рассматриваемую пару других факторов.

Коэффициент корреляционной связи между двумя переменными, xi и x j , очищенной от влияния других переменных называется частным

коэффициентом корреляции. Обозначается Rij,12.... k

Частные коэффициенты корреляции могут быть найдены следующим образом. Пусть R – матрица парных коэффициентов корреляции, а С– матрица обратная к R

Из общей формулы легко получить частные формулы для различного числа переменных. Так для трех переменных можно найти, что частный коэффициент корреляции между переменными x1 и x2 :

Опираясь на эти формулы нетрудно заметить, что парные коэффициенты корреляции могут существенно отличаться от частных. Поэтому для более обоснованного вывода о корреляции между парами факторных переменных

переменной в дисперсию переменной Y.

Однако, не существует единого правила, в соответствии с которым есть некоторое пороговое значение коэффициента корреляции (общего или

39

частного) после которого высокая корреляция может вызвать отрицательный эффект и повлиять на качество регрессии. Для выявления мультиколлинеарности имеются специальные методы8.

Следует отметить, что необходимость выявления и устранения мультиколлинеарности определяется целями исследования. Если основная задача–прогнозирование по модели, то при достаточно большом коэффициенте детерминации наличие мультиколлинеарности чаще всего не сказывается на прогнозных качествах модели, если и в будущем между коррелированными переменными будут сохраняться те же отношения, что и ранее.

Если же целью исследования является определение степени влияния переменных на результативный показатель, то наличие мультиколлинеарности, приводящее к увеличению стандартных ошибок, наверняка исказит истинные зависимости между переменными. В этом случае необходимо подумать об устранении мультиколлинеарности.

Для устранения мультиколлинеарности или ее уменьшения используют различные приемы:

увеличение объема выборки, так как это ведет к уменьшению дисперсии оценок МНК.

исключение из уравнения одной или нескольких объясняющих переменных. В этом случае возникает следующая проблема: возможно переменные были включены на теоретической основе и будет неправомочным их исключение только лишь для того, чтобы сделать статистические результаты лучше. Существуют и другие способы устранения или уменьшения влияния мультиколлинеарности. Единого метода устранения мультиколлинеарности, пригодного для любого случая, не существует. Это связано с тем, что причины

ипоследствия мультиколлинеарности неоднозначны и во многом зависят от выборки.

5. Моделирование временных рядов

5.1. Введение в анализ временных рядов

Наблюдения над некоторым явлением, характер которого меняется во времени, порождает упорядоченную последовательность значений некоторой числовой характеристики этого явления, называемую временным рядом. Значение исследуемой величины в каждый момент времени (или временной интервал) t называется уровнем ряд. Число уровней определяет длину временного ряда..

Теоретически измерения уровней ряда могут регистрироваться непрерывно (временные ряды с непрерывным временем), но обычно они осуществляются через равные промежутки времени (дискретные ряды) и нумеруются аналогично выборке объема n : Yt1 ,Yt2 ,....Ytn . В экономической

8 В.С.Мхитарян и др. Эконометрика,М. Проспект,2008г, стр.77.

40