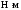- •Введение
- •1. Правила выполнения курсовой работы
- •Принятые обозначения
- •2. Правила сдачи курсовой работы
- •3. Правила оформления курсовой работы
- •4. Задания на курсовую работу Задание 1. Определение реакций связей составных конструкций
- •Задание 2. Кинематический анализ многозвенного механизма
- •Задание 3. Исследование движения механических систем с помощью теоремы об изменении кинетической энергии системы
- •Задание 4. Исследование движения механических систем с помощью методов аналитической механики
- •Задание 5 (дополнительное). Определение сил реакций составной конструкции с помощью принципа возможных перемещений (пвп)
- •Приложение а
- •Форма титульного листа курсовой работы
- •Расчетно-пояснительная записка
- •201__ Приложение б
- •Форма бланка задания на курсовую работу
- •Приложение в
- •Пример оформления содержания
- •Приложение г
- •Примеры библиографических описаний
- •Приложение д
- •Статика Силы реакции связей
- •Распределенные силы
- •Алгебраический момент силы относительно точки
- •Теорема Вариньона для плоской системы сил
- •Условия равновесия плоской системы сил
- •Составная конструкция (сочлененная система тел)
- •Приложение е
- •Кинематика
- •Поступательное движение твердого тела
- •Вращение твердого тела вокруг неподвижной оси
- •Плоское (плоскопараллельное) движение твердого тела
- •Теорема о проекциях скоростей
- •Приложение ж
- •Динамика Работа силы
- •Примеры вычисления работы силы
- •Кинетическая энергия
- •Теорема об изменении кинетической энергии системы
- •Приложение и
- •Аналитическая механика Возможные перемещения
- •Элементарная работа силы на возможном перемещении. Идеальные связи
- •Принцип возможных перемещений (принцип Лагранжа)
- •Обобщенные координаты системы
- •Обобщенные силы
- •Вычисление обобщенной силы
- •Общее уравнение динамики (принцип Даламбера-Лагранжа)
- •Уравнения Лагранжа второго рода
- •Заключение
- •Контрольные вопросы и дополнительные задания Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Библиографический список
- •Оглавление
- •394026 Воронеж, Московский просп., 14
Задание 4. Исследование движения механических систем с помощью методов аналитической механики
Механическая
система состоит из однородных ступенчатых
шкивов 1 и 2, обмотанных нитями, грузов
3–6, прикрепленных к этим нитям, и
невесомого блока (рис. 4.0–4.9, табл. 6).
Система движется в вертикальной плоскости
под действием сил тяжести и пары сил с
моментом
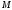 ,
приложенной к одному из шкивов. Радиусы
ступеней шкива 1 равны:
,
приложенной к одному из шкивов. Радиусы
ступеней шкива 1 равны: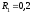 м,
м,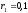 м, а шкива 2 –
м, а шкива 2 –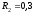 м,
м,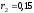 м; их радиусы инерции относительно осей
вращения равны соответственно
м; их радиусы инерции относительно осей
вращения равны соответственно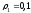 м и
м и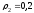 м.
м.
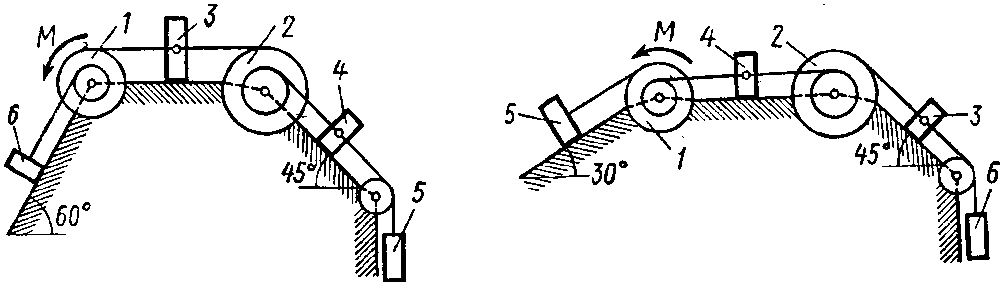
Рис. 4.0 Рис. 4.1
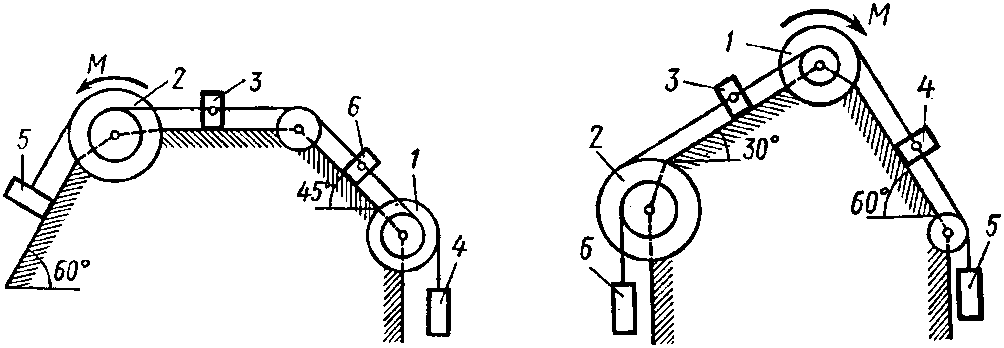
Рис. 4.2 Рис. 4.3
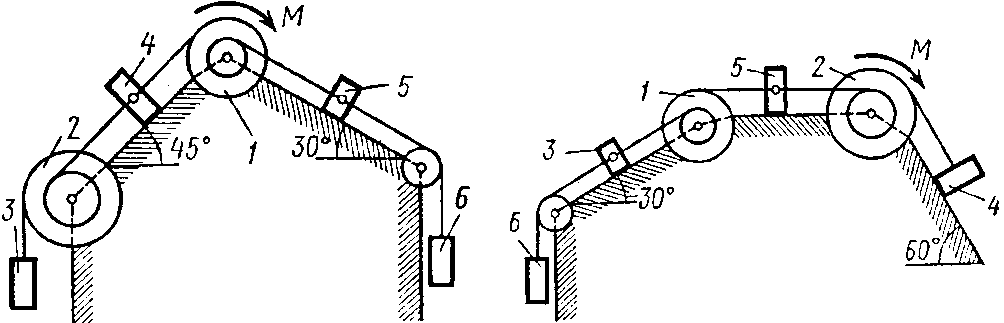
Рис. 4.4 Рис. 4.5
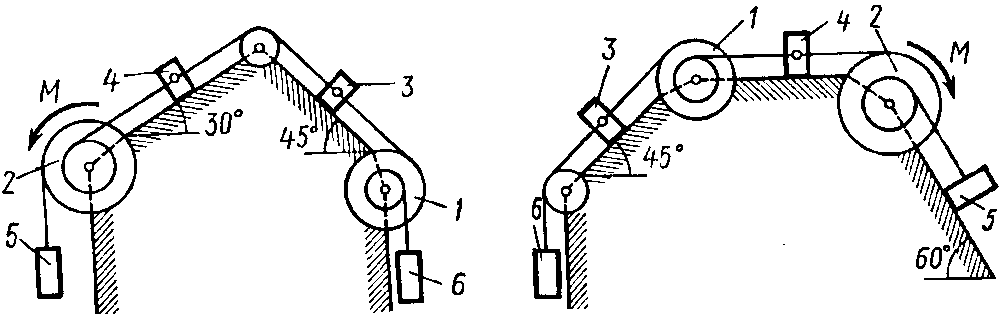
Рис. 4.6 Рис. 4.7
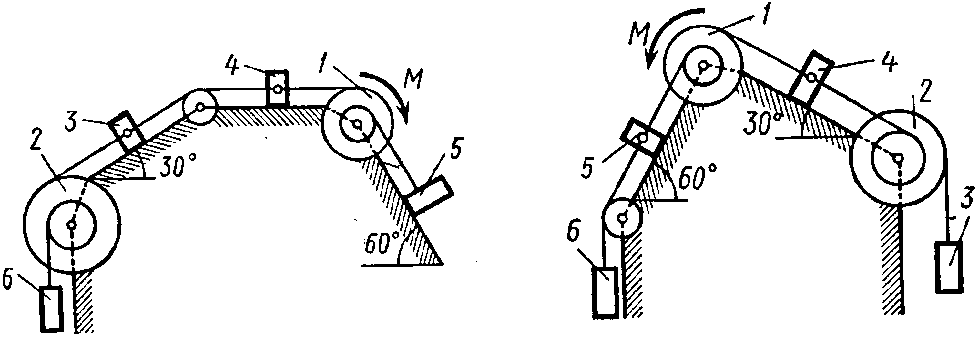
Рис. 4.8 Рис. 4.9
Пренебрегая
трением, найти ускорение груза, имеющего
больший вес; веса
 шкивов и грузов заданы в таблице. Грузы,
веса которых равны нулю, на чертеже
можно не изображать (шкивы 1, 2 изображать
всегда как части системы).
шкивов и грузов заданы в таблице. Грузы,
веса которых равны нулю, на чертеже
можно не изображать (шкивы 1, 2 изображать
всегда как части системы).
Таблица 6
|
Номер условия |
|
|
|
|
|
|
|
|
0 |
10 |
0 |
20 |
30 |
40 |
0 |
10 |
|
1 |
0 |
40 |
0 |
10 |
20 |
30 |
12 |
|
2 |
20 |
30 |
40 |
0 |
10 |
0 |
16 |
|
3 |
0 |
20 |
10 |
30 |
0 |
40 |
18 |
|
4 |
30 |
0 |
20 |
0 |
40 |
10 |
12 |
|
5 |
0 |
10 |
30 |
40 |
20 |
0 |
16 |
|
6 |
40 |
0 |
0 |
20 |
30 |
10 |
10 |
|
7 |
10 |
20 |
0 |
40 |
0 |
30 |
18 |
|
8 |
0 |
40 |
10 |
0 |
30 |
20 |
12 |
|
9 |
30 |
0 |
40 |
20 |
10 |
0 |
16 |
Указания. Задание 4 решается с помощью двух методов аналитической механики – общего уравнения динамики (принципа Даламбера-Лагранжа) и уравнений Лагранжа II рода (см. приложение И).
При
решении с помощью общего уравнения
динамики надо присоединить к действующим
на систему силам соответствующие силы
инерции. Учесть при этом, что для
однородного тела, вращающегося вокруг
своей оси симметрии (шкива), система сил
инерции приводится к паре с моментом
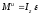 ,
где
,
где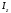 – момент инерции тела относительно оси
вращения,
– момент инерции тела относительно оси
вращения, – угловое ускорение тела; направление
– угловое ускорение тела; направление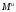 противоположно направлению
противоположно направлению .
Ход решения задачи приведен на примере
4.
.
Ход решения задачи приведен на примере
4.
Решая
задачу методом уравнений Лагранжа, надо
учесть, что система имеет одну степень
свободы, ее положение определяется
одной обобщенной координатой и для нее
должно быть составлено одно уравнение
движения. В задачах, где требуется найти
ускорение груза 3 (4, 5 или 6), за обобщенную
координату удобно принять координату
 ,
характеризующую перемещение этого
груза. Для составления уравнения Лагранжа
необходимо найти кинетическую энергию
,
характеризующую перемещение этого
груза. Для составления уравнения Лагранжа
необходимо найти кинетическую энергию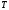 системы и выразить все входящие в нее
скорости через обобщенную скорость
системы и выразить все входящие в нее
скорости через обобщенную скорость ,
а затем вычислить обобщенную силу
,
а затем вычислить обобщенную силу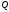 .
Для этого надо сообщить системе возможное
(малое) перемещение, при котором выбранная
координата
.
Для этого надо сообщить системе возможное
(малое) перемещение, при котором выбранная
координата получит приращение
получит приращение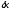 ,
и составить уравнение работ всех сил
на этом перемещении. Коэффициент при
,
и составить уравнение работ всех сил
на этом перемещении. Коэффициент при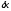 в выражении элементарной работы и будет
искомой обобщенной силой. Дальнейший
ход решения задачи разъяснен в примере
5.
в выражении элементарной работы и будет
искомой обобщенной силой. Дальнейший
ход решения задачи разъяснен в примере
5.
Пример 4
Механическая
система (рис. 4.10) состоит из обмотанных
нитями блока 1 радиуса
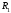 и ступенчатого шкива 2 (радиусы ступеней
и ступенчатого шкива 2 (радиусы ступеней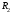 и
и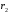 ,
радиус инерции относительно оси вращения
,
радиус инерции относительно оси вращения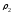 ),
и из грузов 3 и 4, прикрепленных к этим
нитям.
),
и из грузов 3 и 4, прикрепленных к этим
нитям.
Рис. 4.10
Система
движется в вертикальной плоскости под
действием сил тяжести и пары сил с
моментом
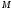 ,
приложенной к блоку 1.
,
приложенной к блоку 1.
Дано:
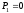 Н,
Н,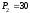 Н,
Н,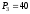 Н,
Н,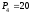 Н,
Н,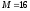
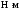 ,
,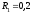 м,
м,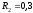 м,
м,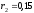 м;
м;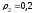 м.
м.
Определить: ускорение груза 3, пренебрегая трением.
Решение:
1. Рассмотрим движение механической системы, состоящей из тел 1, 2, 3, 4, соединенных нитями. Система имеет одну степень свободы. Связи, наложенные на эту систему, – идеальные.
Для
определения
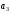 применим общее уравнение динамики:
применим общее уравнение динамики:
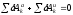 , (1)
, (1)
где
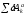 – сумма элементарных работ активных
сил;
– сумма элементарных работ активных
сил;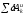 – сумма элементарных работ сил инерции.
– сумма элементарных работ сил инерции.
2.
Изображаем на чертеже активные силы
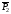 ,
,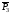 ,
,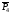 и пару сил с моментом
и пару сил с моментом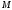 .
Сообщим системе возможное перемещение
.
Сообщим системе возможное перемещение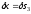 и составим выражение для суммы работ:
и составим выражение для суммы работ:
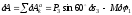 .
.
Выразим
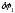 через
через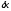 :
:
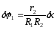 .
.
В результате получим
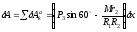 . (2)
. (2)
3.
Задавшись направлением ускорения
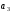 ,
изображаем на чертеже силы инерции
,
изображаем на чертеже силы инерции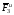 ,
,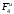 и пару сил инерции с моментом
и пару сил инерции с моментом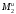 ,
величины которых равны:
,
величины которых равны:
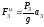 ,
,
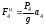 ,
,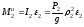 . (3)
. (3)
Сообщая
системе возможное перемещение
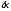 ,
получим:
,
получим:
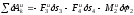 . (4)
. (4)
Выразим
все ускорения, входящие в (3) через искомую
величину
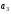
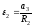 ,
,
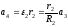 ,
,
а
перемещения через
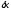 :
:
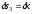 ,
,
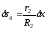 ,
,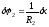 .
.
В результате получим:
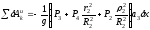 . (5)
. (5)
Подставив
величины
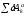 и
и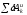 (формулы (2) и (5)) в уравнение (1), и сократив
на
(формулы (2) и (5)) в уравнение (1), и сократив
на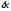 ,
найдем:
,
найдем:
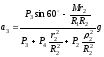 . (6)
. (6)
Вычисления
дают
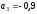 м/с2.
Знак указывает, что ускорение груза 3 и
ускорения других тел направлены
противоположно показанным на рис. Д5.
м/с2.
Знак указывает, что ускорение груза 3 и
ускорения других тел направлены
противоположно показанным на рис. Д5.
Ответ:
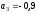 м/с2,
ускорение груза 3 и ускорения других
тел направлены противоположно показанным
на рисунке.
м/с2,
ускорение груза 3 и ускорения других
тел направлены противоположно показанным
на рисунке.
Пример 5
Условие задачи то же самое, что и в примере 4.
Решение:
1.
Система имеет одну степень свободы.
Выберем в качестве обобщенной координаты
перемещение
 груза 3, полагая, что он движется вниз и
отсчитывая
груза 3, полагая, что он движется вниз и
отсчитывая в сторону движения (Рис. Д5). Составим
уравнение Лагранжа:
в сторону движения (Рис. Д5). Составим
уравнение Лагранжа:
 . (1)
. (1)
2. Определим кинетическую энергию всей системы, равную сумме кинетических энергий всех тел:
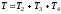 . (2)
. (2)
Грузы 3 и 4 движутся поступательно, поэтому шкив 2 вращается вокруг неподвижной оси, следовательно
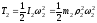 ,
,
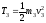 ,
,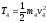 .
(3)
.
(3)
Скорости
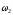 ,
,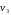 и
и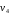 выразим через обобщенную скорость
выразим через обобщенную скорость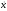 :
:
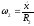 ,
,
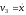 ,
,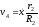 . (4)
. (4)
Подставляя
значения величин (4) в равенства (3), а
затем значения
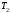 ,
,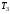 и
и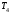 в соотношение (2), получим:
в соотношение (2), получим:
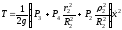 . (5)
. (5)
Так
как кинетическая энергия зависит только
от
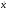 ,
производные левой части уравнения (1)
примут вид:
,
производные левой части уравнения (1)
примут вид:
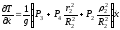 ,
,
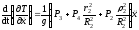 ,
,
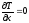 . (6)
. (6)
3.
Найдем обобщенную силу
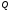 .
Для этого составим уравнение работ
активных сил на перемещении
.
Для этого составим уравнение работ
активных сил на перемещении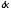 .Воспользуемся
соотношением (2) задачи Д5а:
.Воспользуемся
соотношением (2) задачи Д5а:
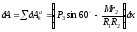 . (7)
. (7)
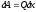 .
.
Коэффициент
при
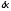 в (7) и будет обобщенной силой:
в (7) и будет обобщенной силой:
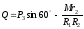 . (8)
. (8)
Подставляя (6) и (8) в уравнение (1), получим
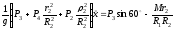 .
.
Отсюда находим
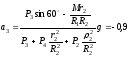 м/с2,
м/с2,
что совпадает с ответом примера 4 .
Ответ:
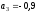 м/с2,
что ускорение груза 3 и ускорения других
тел направлены противоположно показанным
на рисунке.
м/с2,
что ускорение груза 3 и ускорения других
тел направлены противоположно показанным
на рисунке.

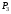
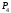
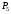
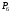
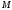 ,
,