Теория графов

Учебное издание

Ююкин Николай Алексеевич

ДИСКРЕТНАЯ МАТЕМАТИКА Часть 1. Элементы теории графов

ЛР № . Подписано в печать

. Уч. Изд. л.. , .

Воронежский государственный технический университет

394026 Воронеж, Московский просп. 14

0

СПРАВОЧНИК МАГНИТНОГО ДИСКА

Кафедра высшей математики и физико-математического моделирования

Н.А. Ююкин

ДИСКРЕТНАЯ МАТЕМАТИКА Часть 1. Элементы теории графов

Учебное пособие

1

Н.А. Ююкин

ДИСКРЕТНАЯ МАТЕМАТИКА Часть 1. Элементы теории графов

Учебное пособие

Воронеж 2004

2

ВВЕДЕНИЕ

Данное пособие может быть использовано в курсе “Дискретная математика” студентами ВГТУ, обучающимися по специальностям:

090102 – Компьютерная безопасность;

090105 – Комплексное обеспечение информационной безопасности автоматизированных систем;

090106 - Информационная безопасность телекоммуникационных систем.

Дисциплина “Дискретная математика” обеспечивает приобретение знаний и умений в соответствии с государственным, общеобразовательным стандартом, и при этом содействует получению фундаментального образования, формированию мировоззрения и развитию логического мышления.

Теория графов является эффективным аппаратом формализации современных инженерных задач, связанных с дискретными объектами. Она используется при проектировании интегральных схем и схем управления, исследовании автоматов и логических цепей, в системном анализе, автоматизированном управлении производством, при разработке вычислительных и информационных сетей, в схемотехническом и кон- структорско-топологическом проектировании и т.д.

В учебном пособии излагаются основы, базовые методы и алгоритмы теории графов. Здесь представлены н-графы и орграфы; изоморфизмы; деревья; эйлеровы графы; планарные графы; покрытия и независимые множества; сильная связность

ворграфах; анализ графа цепи Маркова; алгоритмы поиска кратчайших путей в графах; задача поиска гамильтонова цикла

вграфе; задача о коммивояжере; перечисление графов и отображений; экстремальные задачи; оптимизационные задачи; универсальные задачи; метод ветвей и границ; а также вырабатываются практические навыки по использованию вышеприведенных понятий.

Целью курса является формирование у студентов теоретических знаний, практических умений и навыков в области моделирования процессов и явлений в естествознании и техни-

3

ке, с возможностью употребления математических символов для выражения количественных и качественных отношений объектов, необходимых для выполнения служебной деятельности в области защиты информации на высоком профессиональном уровне.

Достижению данной цели служат следующие задачи:

изучить максимально широкий круг понятий теории графов;

получить навыки решения учебных и практических задач;

овладеть методами оптимизации;

выработать навыки постановки и решения информационных задач, моделирования и анализа информации с помощью графов.

Дисциплина “Дискретная математика” относится к числу прикладных математических дисциплин. Она основывается на знаниях, приобретенных студентами при изучении дисциплин “Алгебра” и “Математическая логика и теория алгоритмов”. Знания и навыки, полученные при изучении дисциплины “Дискретная математика” используются при изучении общепрофессиональных и специальных дисциплин.

4

1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРАФОВ.

1.1. Задачи теории графов.

Теория графов - это раздел математики, изучающий системы связей между различными объектами, точно так же как это делается с помощью понятия отношения. Однако независимое определение графа упрощает изложение теории и делает её более понятной и наглядной.

Первые задачи теории графов были связаны с решением развлекательных задач и головоломок.

Первая задача. Задача о Кенигсбергских мостах была поставлена и решена Эйлером в 1786 году. Город располагался на берегах и двух островах реки Преголи. Острова между собой и берегами были связаны семью мостами, как показано на рисунке.

Возникал вопрос: можно ли выйдя из дома, вернуться обратно, проходя по каждому мосту ровно один раз?

Вторая задача. Задача о трех домах и трех колодцах. Имеется три дома и три колодца.

Требуется провести от каждого дома к каждому колодцу тропинку так, чтобы тропинки не пересекались. Задача была

5

решена Понтрягиным и независимо от него Куратовским в

1930 году.

Третья задача. О четырех красках. Любую карту на плоскости раскрасить четырьмя красками так, чтобы никакие две соседние области не были закрашены одним цветом.

4

3

Многие результаты теории графов используются для решения практических задач науки и техники. Так, в середине 19 века Кирхгоф применил теорию графов для расчета сложных электрических цепей. Однако, как математическая дисциплина, теория графов сформировалась только в 30-ых годах 20го века. При этом графы рассматриваются как некоторые абстрактные математические объекты. Они применяются при анализе и синтезе цепей и систем, в сетевом планировании и управлении, исследовании операций, программировании, моделировании жизнедеятельности организма и других областях.

1.2. Основные определения.

Графом G=(V,E) называется совокупность двух множеств - непустого множества вершин V и множества неупорядоченных и упорядоченных пар вершин E. В дальнейшем будут рассматриваться конечные графы, т.е. графы с конечным множеством вершин и конечным семейством пар. Неупорядоченная пара вершин называется ребром, а упорядоченная - дугой.

Обычно граф изображается диаграммой: вершины - точками (или кружками), ребра – линиями произвольной конфигурации. На дуге дополнительно стрелкой указывается её направление. Отметим, что при изображении графа несуще-

6

ственны геометрические свойства ребер (длина, кривизна), а также взаимное расположение вершин на плоскости.

Вершины, которые не принадлежат ни одному ребру (дуге) называются изолированными. Вершины, соединенные ребром или дугой называются смежными. Ребро (дуга) и любая из его двух вершин называются инцидентными.

Говорят, что ребро (u,v) соединяет вершины u и v, а дуга (u,v) начинается в вершине u и заканчивается в вершине v, при этом u называется началом, а v – концом этой дуги.

Граф, содержащий только ребра, называется неориентированным (неорграф, н-граф). Граф, содержащий только дуги, называется ориентированным (орграфом). Граф называется смешанным, если в нём одновременно присутствуют и ребра и дуги.

Пара вершин может соединяться двумя или более ребрами (дугами одного направления). Такие ребра (дуги) называются кратными. Дуга (или ребро) может начинаться или кончаться в одной и той же вершине. Такая дуга (ребро) называется петлёй. Граф, содержащий петли, называется псевдо графом. Граф, имеющий кратные ребра (дуги), называется мультиграфом.

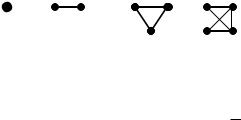
Граф, без петель и кратных ребер, называется простым. Простой граф называется полным, если для любой пары его вершин существует ребро (дуга) их соединяющая. Полный граф, имеющий n вершин обозначается через Kn. Например, это графы

Граф, состоящий из одной изолированной вершины (K1), называется тривиальным.

Дополнением графа G называется граф G , имеющий те же вершины, что и граф G и содержащий те ребра, которые нужно добавить к графу G чтобы получить полный граф.

7

Каждому неорграфу канонически соответствует ориентированный граф с тем же множеством вершин, в котором каждое ребро заменено двумя дугами, инцидентными тем же вершинам и имеющих противоположные направления.

1.3. Степени вершин графа.

Степенью (валентностью) (обозначение d(v) или deg(v)) вершины v простого графа G называется число ребер или дуг инцидентных данной вершине v. При подсчете валентности вершин псевдографа следует учитывать каждую петлю дважды.

Если степени всех вершин н-графа равны k, то граф называется регулярным (однородным) степени k. Если степень вершины равна 0, то она является изолированной. Если степень вершины равна 1, то вершина называется концевой (висячей, тупиковой).

Для орграфа число дуг исходящих из вершины v назы-

Теорема Эйлера: Сумма степеней вершин графа равна

ребер (дуг). Данное утверждение доказывается тем, что при подсчете суммы степеней вершин каждое ребро учитывается два раза - для одного конца ребра и для другого.

1.4. Изоморфизм графов.

Граф называется помеченным (или перенумерованным), если его вершины отличаются друг от друга какими либо по-

8

метками (номерами). Граф считается полностью заданным в строгом смысле, если нумерация его вершин и ребер фиксирована. При этом графы G1 и G2 называются равными (обозначение G1 = G2), ,если их множества вершин и ребер совпадают. Два графа или псевдографа G1=(V1,E1) и G2=(V2,E2) называют-

оказываются изоморфными, если существуют взаимно одно-

Таким образом, изоморфными являются графы, которые отличаются только нумерацией вершин и ребер. Изоморфизм графов представляет собой отношение эквивалентности, поскольку оно обладает свойствами:

2 ( 1 ) .

9