Теория графов

другому. Следовательно, условие отсутствия вершин нечетной степени является необходимым.

Достаточность. Предположим, что все вершины связного графа G имеют чётные степени. Тогда, в силу связности графа G, для всех его вершин выполняется условие d(v)>0. Кроме того, в силу чётности вершин, должно быть d(v) 2 для

n

всех v. По теореме Эйлера имеем: 2m d (vi ) 2n .Это зна-

ется деревом, а поэтому он содержит хотя бы один простой цикл Z1 (Z1 - множество ребер), тогда G\Z1 – остовный подграф, в котором все степени вершин также четные. Исключим из рассмотрения изолированные вершины, тогда в графе G\Z1 существует простой цикл Z2 G\Z1, далее выделим Z3 и т.д. В результате этого получается разбиение множества ребер на про-

стые циклы, то есть: E Zi ,где Zi .

наращивать эйлеров цикл до тех пор, пока не исчерпаем всё разбиение. В результате получаем эйлеров цикл всего графа.

5. 2. Алгоритм построения эйлерова цикла в эйлеровом графе.

Этот алгоритм задается следующими правилами: 1) Выбирается произвольная вершина v.

30

2)Выбирается ребро e инцидентное вершине v и ему присваивается номер 1 (это ребро называется пройденным).

3)Каждое пройденное ребро вычеркивается и ему присваивается номер на 1 больший номера предыдущего вычеркнутого ребра.

4)При нахождении в произвольной вершине x, не выбирается ребро, соединяющее x с v, если есть возможность другого выбора.

5)Ребро не проходится, если оно является перешейком. Перешейк – это ребро, при удалении которого, граф, образованный невычеркнутыми ребрами, распадается на две компоненты связности, каждая из которых имеет хотя бы одно ребро.

6)После того, как в графе будут занумерованы все ребра, образуется эйлеров цикл, нумерация рёбер которого соответствует последовательности обхода

ребер.

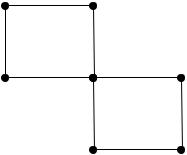
Пример. Найти эйлеров цикл в эйлеровом графе

4

5

3

2

6

1

7

8 v

После выбора вершины v и прохождения рёбер 1 и 2 имеется три возможности: выбрать 3,6 или 7. Ребро 7 является перешейком, поэтому выбирается любое из оставшихся рёбер, например 3. Далее идёт обход оставшихся рёбер получается эйлеров цикл.

31

5.3. Гамильтоновы графы.

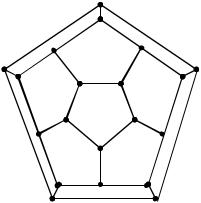
Название «гамильтонов граф» произошло от задачи «кругосветное путешествие», придуманной Гамильтоном в 19 веке. Нужно обойти все вершины графа, изображенного на рисунке, по одному разу и вернуться в исходную точку.

Гамильтоновой цепью неорграфа называется цепь, проходящая через его вершину один и только один раз.

Гамильтоновым циклом неорграфа называется цикл, проходящий через каждую вершину один и только один раз, за исключением начальной вершины, совпадающей с конечной.

Граф, содержащий гамильтонов цикл называется гамильтоновым.

Гамильтоновым контуром называется контур орграфа, который проходит через все его вершины, причем только по одному разу.

Эйлеровы и гамильтоновы циклы сходны по способу задания. Эйлеровы содержат все ребра по одному разу, а гамильтоновы – все вершины так же по одному разу. Несмотря на это внешнее сходство, задачи отыскания соответствующих циклов резко отличаются. Так для решения вопроса о существовании эйлерова цикла, достаточно выяснить четность всех вершин графа. Эффективного критерия существования гамильтонова цикла пока ещё не найдено. Известны лишь несколько

32

теорем, дающих достаточные условия существования гамильтоновых циклов.

Теорема 1. В полном, конечном графе (любая пара вершин которого соединена хотя бы в одном направлении) всегда существует гамильтонов цикл.

Теорема 2. Если для любой пары несмежных вершин vi и vj графа G с n вершинами справедливо неравенство d(vi)+d(vj) n , то граф обладает гамильтоновым циклом.

Теорема 3. Граф G с n вершинами имеет гамильтонов цикл, если для любой вершины vi выполняется неравенство d(vi) n\2,где n – число вершин в графе.

5.4. Оценки числа эйлеровых и гамильтоновых графов.

Теорема. В любом графе число вершин нечетной степени всегда четно.

значит, что сумма степеней всех вершин графа есть четное число. Сумма степеней вершин чётной степени также чётна, следовательно, будет чётна сумма степеней вершин нечётной степени. Это значит, что их число четное.

Пусть G(n) есть множество всех возможных графов с n вершинами, E(n) – множество эйлеровых графов с n вершина-

почти нет. С другой стороны почти все графы – гамильтоновы,

графов с n вершинами.

Задача отыскания гамильтонова цикла является практически востребованной, однако для нее неизвестны, а скорее всего не существует эффективные алгоритмы решения.

33

6. ФУНДАМЕНТАЛЬНЫЕ ЦИКЛЫ И РАЗРЕЗЫ.

6.1. Фундаментальные циклы.

Пусть G=(V, E) – неорграф , имеющий n вершин и m ребер и c – компонент связности. Пусть Т – остов графа G. Остов имеет n-c ребер, обозначенных как u1, ,un c . Эти ребра назы-

ваются ветвями остова Т. Оставшиеся m-n+с ребер , не входящие в остов Т, называются хордами

остова Т. Если к лесу Т добавить произвольную хорду vi, то в полученном графе образуется ровно один простой цикл, обозначенный Ci. Этот цикл состоит из некоторых ветвей остова Т

циклов, относительно хорд остова Т, называется фундаментальным множеством циклов графа G, относительно остова Т. Мощность фундаментального множества циклов не зависит от выбора остова Т и равна цикломатическому числу ν(G)=m-n+c.

Обозначим через (1, 2, …, m) последовательность (v1, v2, …, vm-n+c, u1, u2, …, un-c) всех ребер графа G. Тогда фундаментальному циклу Ci соответствует вектор a (ai1, ai 2 , , aim ) ,

координаты которого определяются по правилу:

Таким образом, фундаментальное множество циклов задается с помощью матрицы фундаментальных циклов, строки

34

Так как, каждый фундаментальный цикл Ci содержит ровно одну хорду vi, то матрица С имеет следующий вид:

ца, порядка v(G).

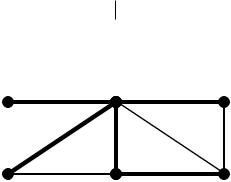
Пример. Найти матрицу фундаментальных циклов графа G, изображенного на рисунке

1

7

Цикломатическое число графа - v(G)=m-n+c=8-6+1=3. Следовательно, для получения остова, необходимо удалить из графа три ребра. Пусть этими ребрами будут 1, 2, 3 (удаляем так, чтобы в остове не было циклов). Ребрами, входящими в остов, присваиваются номера 4, 5, 6, 7, 8. Они на рисунке изображены жирными линиями. В результате фундаментальный цикл С1, соответствующий хорде 1, состоит из ребер 1, 4 и 6. Цикл С2 – из рёбер 2, 6, 7; цикл :С3 – из рёбер 3, 6, 7, 8. В результате этого, матрица фундаментальных циклов будет иметь вид:

35

6.2. Разрезы.

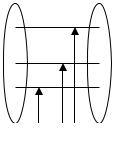
Пусть G=(V,E) – неорграф, V ={V1, V2} – разбиение множеств V. Разрезом графа G (по разбиению V) называется множество всех ребер, соединяющих вершины из V1 с вершинами из V2.

V1 Разрез V2

Заметим, что в связном графе любой разрез непуст. Непустой разрез K неориентированного графа G называется коциклом

гими словами из К нельзя удалить ни одно ребро с тем, чтобы полученное множество было непустым разрезом.

Заметим, что понятие остова и коцикла является противоположными в том смысле, что остову соответствует минимальное количество ребер, которые связывают посредствам маршрутов все вершины связного графа, а коцикл состоит из минимального количества ребер, отделяющих некоторые вершины связного графа от остальных вершин.

Теорема 1. В конечном неорграфе G=(V, E), имеющим c компонент связности, множество ребер К тогда и только тогда является коциклом, когда граф (V, E\K) имеет c+1 компонент связности.

Теорема 2. В связном неорграфе остовное дерево имеет по крайней мере одно общее ребро с любым из разрезов графа.

Теорема 3. В связном неорграфе любой цикл имеет с любым разрезом четное число общих ребер.

36

Рассмотрим неорграф G=(V, E) имеющий n вершин, m ребер и c компонент связности. Пусть Т – остов графа G и u1, u2, …, un-c – множество ветвей остова Т. Удаляя из остова Т произвольную ветвь ui, получим лес с (c+1) компонентами

ui

связности, т.е. ребро ui является разрезом остова Т по некоторому разбиению {V1, V2}.

В графе G могут существовать ещё какие-то ребра vi1, vi2, …, vij, являющиеся хордами остова Т, соединяющие вершины из V1 с вершинами из V2. Множество рёбер Кi={ui, vi1, vi2, …, vij} образует простой разрез графа. Он называется фундаментальным разрезом графа G, относительно ветви ui остова Т. Множество {K1, K2…,Kn-c} всех фундаментальных разрезов графа G, относительно остова T, называется фундаментальным множеством коциклов графа G, относительно остова Т. Мощность этого множества не зависит от выбора остова Т и равна

n-c. Число (G) n c называется корангом. Фундаментальному разрезу Ki ставится в соответствие

Фундаментальное множество коциклов задается матрицей фундаментальных разрезов, строки которой являются век-

торами b1,b2 , ,bn c .

37

Так как, каждый фундаментальный разрез Ki содержит ровно одну ветвь, а именно ui, то матрица К имеет следующий вид:

Таким образом, матрицу К можно представить в виде

ном графе имеется пять фундаментальных разрезов (коциклов). Ребро 4 соответствует коциклу К1={1, 4}, поскольку при удалении ребра 4 из остова Т множество вершин V разбивается на две части {v1} и V\{v1}. А на разбиении {{v1}, {V\{v1}}} рёбра 1 и 4 образуют разрез. Аналогично ребру 5 соответствует коцикл К2={5}, ребру 6 соответствует коцикл K3={1, 2, 3, 6}, ребру 7 соответствует коцикл K4={2, 3, 7} и ребру 8 соответствует ко-

38

цикл K5={3, 8}. Таким образом, матрица фундаментальных разрезов имеет вид:

39