
Теория графов
.pdf
(ai aj)
d(1)j
kj
ai
d(1)k
ak
Продолжая этот процесс на шаге S определяется строка
Д(3)=(d(3)1, d(3)2, d(3)3, …, d(3)n), в которой d(3)j=min{d(3-1)j, d(3-
1)k+ kj}, k=1,2,…,n
Искомая строка - расстояний получается при S=n-1,
т.е. d(n-1)j= (ai aj).
Действительно, на этом шаге из весов всех (ai, aj) маршрутов выбирается наименьший, а каждый маршрут с более чем n-1 дугами содержит контур, добавление которого к маршруту не уменьшает расстояния т.к. по условию в графе отсутствуют контуры отрицательного веса.
Работу алгоритма можно завершить на K-ом шаге (k<n- 1), если Д(к)=Д(к+1).
60
11. ЗАДАЧА КОММИВОЯЖЕРА.
11.1. Постановка задачи.
Коммивояжер или торговый агент реализует товар в нескольких населенных пунктах, расположенных на определенных расстояниях друг от друга. Коммивояжер должен объехать все эти пункты по кратчайшему маршруту и вернуться обратно. С точки зрения теории графов задача коммивояжера формулируется как задача нахождения гамильтонова цикла минимальной длины.
Многие практические задачи сводятся к задаче коммивояжера. Например:
1.Пусть граф задает сеть коммуникаций между фиксированными центрами. Необходимо построить маршрут, обеспечивающий все центры, проходя через них ровно по одному разу.
2.Имеется станок с числовым программным управлением (ЧПУ), который высверливает отверстия в печатных платах по заданной программе. Составляется граф, вершины которого соответствуют требуемым отверстиям. Необходимо найти такой обход вершин графа, чтобы суммарное время обхода было минимальным.
11.2. Обходы вершин графа по глубине и ширине.
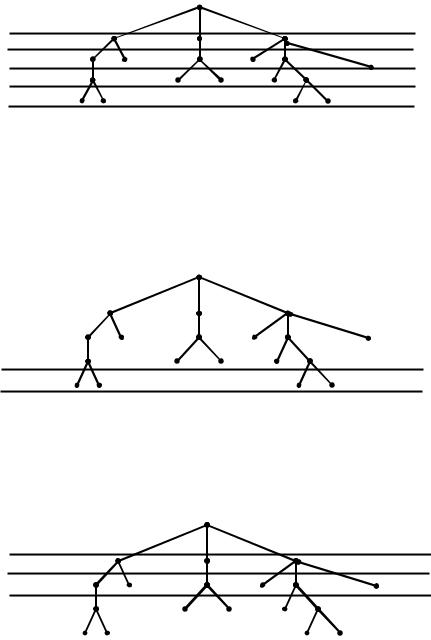
При решении прикладных задач часто возникает необходимость обхода вершин графа, связанная с поиском вершин, удовлетворяющих определенным свойствам. Пусть G(V, E) – связный граф, N – некоторый остов графа G, а – некоторая фиксированная вершина, называемая корнем дерева Т. Разместим вершины из V по этажам таким образом, чтобы корень а находился в верхнем этаже, а смежные с корнем вершины находились на этаж ниже. Вершины, смежные с отмеченными вершинами находятся на этаже еще на единицу ниже и т.д.
61
а
1
2
3
4
5
Рассмотрим обход графа по глубине.
При таком обходе после очередной рассмотренной вершины выбирается смежная с ней вершина следующего этапа. Если очередная рассмотренная вершина висячая и ее достижение не дает желаемого результата, то необходимо вернуться до ближайшей вершины и просмотреть в таком же порядке вершины другого, еще не пройденного, маршрута и т.д.
Например:
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
8 |
|
12 |
|
|
3 |
7 |
9 |
13 |
19 |
14 |
|
|
|
|
|
|
|
|
|
|
4 |
|
10 |
11 |
15 |
16 |
|
|
5 |
6 |
|
|
17 |
18 |
|
При обходе графа по ширине просмотр вершин дерева ведется по этажам. Переход к вершинам следующего этажа производиться только после просмотра всех вершин данного этажа.
|
Например: |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
3 |
|
4 |
|
|
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
|
|
|
|
|
||
|
11 |
12 |
13 |
14 |
|
15 |
|
16 |
17 |
|
18 |
|
19 |
|
|
|
|
|
|
|
|
|
|
62
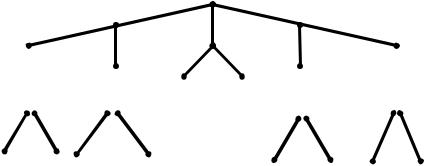
Заметим, что при обходе всех вершин оба подхода эквивалентны. Если же требуется найти одну вершину с определенными свойствами, то целесообразность применения обхода по глубине или ширине определяется структурой дерева. Если дерево достаточно широкое, то висячие вершины расположены на сравнительно близких этажах, поэтому в этом случае целесообразно вести поиск по глубине. Для глубоких и узких деревьев висячие вершины могут находиться на разных этажах, поэтому предпочтение в этом случае отдается поиску по ширине.
При компьютерной реализации обходов по глубине и ширине целесообразно использовать задание дерева структурой смежности вершин.
Часто при решении задач их разбивают на несколько более простых задач, которые в свою очередь разбивают на еще более простые подзадачи и так до тех пор, пока не появляются подзадачи, поддающиеся непосредственному решению. Такое разбиение задач можно представить в виде дерева. Если задача А разбивается на подзадачи А(1,1)А(1,2),…, А(1,n), подзадачи А(1, i) на подзадачи А(2,i,1), A(2,i,2),…, A(2,i,n2i) и т.д. получается следующее дерево.
|
А |
А(1,1) |
А(1,n1) |
|
А(1,2)… |
А(2,1,1) |
A(2,n1,n2n1) |
A(2,1,n21) |
A(2,n1,1)… |
… |
… |
… |
… |
63
Для решения поставленных задач используются обходы таких деревьев с поиском по глубине и по ширине. Рассмотрим данный подход на примере решения задачи Коммивояжера методом ветвей и границ.
11.3. Решение задачи коммивояжера.
Пусть W=( ij) – матрица весов графа G(V,E), не имеющего петель. V={1,2,…,n}. Для простоты считается, что вес всех ij неотрицателен. Предполагается, что ij= , если i=j. Производится нижняя оценка весов гамильтоновых циклов. Для этого в матрице весов находятся минимальные числа каждой строки:1k1, 2k2, …, nkn. Вес произвольного гамильтонова цикла не меньше 1k1+ 2k2+ …+ nkn. Матрица преобразуется путем вычитания из каждой i-ой строки соответствующего числа iki.
В результате получается матрица Wv=( vij), где vij= ij - iki. В полученной матрице ищутся минимальные числа в каждом
столбце v11, v22, …, vinn. Матрица преобразуется путём вычитания из каждого j-го столбца соответствующее i-ое число vijj.
В результате получается матрица W*=(*ij), где *ij= vij- vijj. Для любого гамильтонова цикла X справедлива оценка его веса
(X): (X) h, где h= 1k1+ 2k2+…+ nkn+ vi11+ vi22+…+ vinn.
Далее вводится обозначение (а1, а2, …,ак) {b1,b2,…,bt} – это множество гамильтоновых циклов, в которых первые k вершин
являются а1, а2, …,ак, а следующая k+1 вершина аk+1 не принадлежит множеству {b1,b2,…,bt}.
Используя введенное обозначение, разбиваем задачу на две подзадачи, путем разбиения всего множества гамильтоновых циклов на два множества (1, K1) и (1){K1} т.е. множества гамильтоновых циклов, содержащих
1)вершину 1 и K1
2)вершину 1 и не содержащих K1.
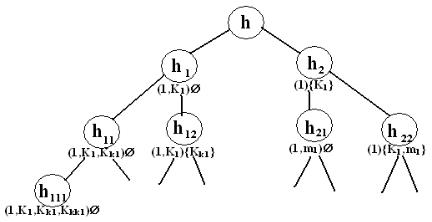
Каждая из этих подзадач делится дальше и т.д. В результате дерево имеет следующий вид:
64
65
При рассмотрении множества (1,K1) отождествим в графе G вершины 1 и K1 и обозначим новую образовавшуюся вершину через x. В результате получается граф G` с множеством вершин {x1,2,…,k1-1,k1+1,…,n}.
Матрица весов имеет следующий вид:
W`=
|
|
|
|
|
|
* |
|
|
|
* |
|
|
... |
|
* |
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
... |
|
* |
|
|
|
||||||||||||
|
|
|
|
k |
|
,2 |
|
k |
|
,3 |
|
k |
1 k1 |
1 |
|
k |
1 k1 |
1 |
|
k |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k1n |
|
||||||||||
|
|
|
|
* |
|
|
|
|
|
|
|
* |
... |
|
|
|
|
* |
|
|
1 |
|
|
|
|
* |
|
|
1 |
... |
|
* |
|
|
|||||||||||||
21 |
|
|
|
23 |
2 |
|
|
k |
1 |
2 |
|
|
k |
1 |
|
2n |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
... |
|
|
|
... |
|
|
|
... |
|
... |
|
|
|
... |
|
|
|
|
|
|
... |
|
|
|
... |
|
|
|
... |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
* |
|
|
|
|
* |
|
|
1,2 |
|
* |
|
|
1,3 |
... |
|
* |
|
|
1,k |
|
1 |
|
* |
|
|
1,k |
|
1 |
... |
|
* |
|
|
1,n |
|
||||||||||
|
|
k 1,1 |
|
k |
|
|
k |
|
k |
|
|
k |
|
|
|
|
k |
|
|
||||||||||||||||||||||||||||
|
|
|
|
i |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
* |
|
1,1 |
|
* |
|
|
1,2 |
|
* |
|
|
1,3 |
... |
|
* |
|
|
1,k |
|
1 |
|
* |
|
|
1,k |
|
1 |
... |
|
* |
|
|
1,n |
|
|||||||||||
|
k |
1 |
|
k |
1 |
|
k |
1 |
k |
1 |
1 |
k |
1 |
1 |
|
|
k |
1 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
... |
|
|
|
... |
|
|
|
... |
|
... |
|
|
|
... |
|
|
|
|
|
|
... |
|
|
|
... |
|
|
|
... |
|
||||||||||||||
|
|
* |
|
|
|
* |
|
|
|
|
* |
|
|
... |
|
* |
|
|
|
1 |
|
|
* |
|
|
|
1 |
|
... |
|
* |
|
|
||||||||||||||
|
|
n1 |
n2 |
|
n3 |
nk |
|
|
n k |
|
|
nn |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для графа G` найдем нижнюю оценку h` весов гамильтоновых циклов аналогично тому, как найдены оценки h. Тогда нижняя оценка h1 весов гамильтоновых циклов множества
(1,K1) равна h+h`.
При рассмотрении множества (1){K1} в матрице весов
W* элемент |
* |
|
заменяется на |
и по полученной матрице |
|
1k1 |
W``` находится нижняя оценка h`` весов гамильтоновых циклов множества (1){K1} равная h+h``.
Каждая из подзадач разбивается на свои подзадачи, и этот процесс с оцениванием весов гамильтоновых циклов продолжается до тех пор пока не отыщется самая низкая из оценок являющаяся весом некоторого гамильтонова цикла, который и будет иметь минимальный вес.
При рассмотрении подзадач целесообразно вести поиск в глубину, при котором на каждом следующем этаже выбирается та подзадача, которая имеет меньшую нижнюю оценку.
66
12.ПОТОКИ В СЕТЯХ.
12.1.Основные определения.
Если в графе ориентировать все ребра, то получится орграф, который называется направленным. Направленный орграф, полученный из полного графа, называется турниром.
Если в орграфе полустепень захода некоторой вершины равна нулю, т.е. d+(V)=0, то такая вершина называется источником, если же нулю равна полустепень исхода, т.е. d-(V)=0, то вершина называется стоком. Направленный орграф без петель с одним источником и одним стоком называется (двухполюсной) сетью.
Пусть G (V, E) – сеть, а S и t – соответственно источник и сток сети. На множестве дуг сети определена неотрицательная функция C: E R+, ставящая каждой дуге (u,v) неотрицательное вещественное число c(u, v), называемое пропускной способностью дуги (u, v).
Пусть задана функция f: E R. Дивергенцией функции f в вершине V называется число div(f,v), которое определяется
следующим образом: |
div(f,v)= |
f (u, v) - |
f (v, u) |
|
|
|
|
{U |(U ,V ) E} |
{U |(V ,U ) E} |
Функция f: E R называется потоком в сети G, если: |
||||
1) |
(u,v) E |
0 f(u,v) C(u,v) |
|
|
2) |
v v\{s,t} div(f,v)=0 |
|
|
|
Число (f)=div(f,s) называется величиной потока f. Замечание. Первое условие в определении потока означает,
что поток через дугу неотрицателен и не превосходит пропускной способности дуги. Второе условие означает, что величина потока, входящего в каждую вершину сети (кроме истока и стока), равно количеству потока, выходящего из этой вершины.
Спомощью потоков в сети можно моделировать:
1)автомобильные потоки на дорогах
2)перекачку нефти на нефтепроводе
67
3)последовательность технологических операций для производства готовых изделий из сырья.
4)передачу информации в компьютерной сети
В данной лекции рассматривается решение только одной (но самой существенной) задачи этой теории – нахождения максимального потока в сети.
Для решения этой задачи сеть разбивается на два непересекающихся множества таким образом, чтобы исток попал в одно множество, а сток – в другое. В этом случае говорят, что на сети произведен разрез, отделяющий исток от стока.
Пусть P – (s,t) разрез, P E. Всякий разрез определяется разбиением множества вершин V на два подмножества A и B так, что A,B V, A B=V, A B=0, s A, t B. Разрез обозначается
P(A) и представляет собой множество дуг |
(U,V) E, таких, что |
|||||
U A, V B. |
|
|
|
|
|
|
|
Пропускной способностью разреза называется сумма |
|||||
пропускных |
способностей |
входящих |
в |
него |
дуг |
|
C\A= |
c(a, v) |
|
|
|
|
|
|
( ,V ) P( A) |
|
|
|
|
|
Минимальным разрезом, разделяющим исток s и сток t сети, называется произвольный разрез P(A) s A, t V\A с минимальной пропускной способностью.
12.2. Теорема Форда и Фалкерсона.
Величина каждого потока от входа к выходу не превосходит пропускной способности минимального разреза, разделяющего вход и выход сети. При этом существует максимальный поток, величина которого равна пропускной способности минимального разреза.
Все известные алгоритмы построения максимального потока основаны на последовательном увеличении потока.
Дуга (U,V) является допустимой, если для нее выполняется одно из условий:
68
1)направление дуги совпадает с направлением потока и значение потока по этой дуге меньше её пропускной способности f(U,V)<C(U,V)
2)направление дуги противоположно направлению потока и по ней проходит некоторый нулевой
поток f(U,V)>0
Дуги, для которых выполняется условие 1), называются увеличивающими или согласованными дугами. Дуги, для которых выполняется условие 2) называются уменьшающими или несогласованными дугами.
Увеличивающей цепью называется простая цепь, соединяющая исток и сток сети, все дуги которой являются допу-
стимыми. |
|
|
|
|
|
|
Знание увеличивающей цепи позволяет увеличить поток |
||||
по |
ней |
на |
величину |
= min { (e)}, |
где |
|
|
|
|
V |
|
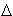 (e)=
(e)=
с(e) f (e), если е увеличиваю щая дуга |
|
|
|
f (e), если e уменьшающа я |
дуга |
При этом по каждой увеличивающей дуге поток увели-
чивается на , а по каждой уменьшающей дуге уменьшается на
.
Такое изменение потока по каждой дуге в сумме компенсируется для каждой вершины сети, отличной от истока и стока, т.е. для любой вершины сети v V\{s,t} по-прежнему будет выполняться div(f,v)=0.
12.3. Алгоритм построения максимального потока.
Шаг 1. Задать начальное значение потока, если оно не задано. Удобно задавать начальное значение потока равным нулю. Перейти на шаг 2.
Шаг 2. Построить увеличивающую цепь от истока к стоку сети. Если увеличивающей цепи не существует, то максимальный поток построен, его значение: (t)=div(f,s), в противном случае перейти на шаг 3.
69
