
Теория графов
.pdf
Затем выписывается уравнение связи переменных тока и напряжения.
Рассмотрим первый этап процесса. Применяя к вершине Vi
правило вершин, получим:
m |
|
aij x j |
0 |
j 1 |
|
,где
|
|
|
1, если |
i |
вершины |
положительно инциденты |
j |
дуг е |
a |
|
|
|
i |
вершины |
отрицательно инциденты |
j |
дуг е |
ij |
1, если |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
инцидентные |
случаи отсутствуют |
|
|
|
|
|
|
0, если |
|
|
|||
|
|
|
|
|
|
|
|
|
т.е. векторы Ai=(ai1,ai2,…,aim) и X`=(x1,…,xm) являются ортогональными.
Здесь Ai есть строки матрицы смежности A. Так как пространство натянутое на строке A совпадает с пространством, натянутым на строки матрицы разрезов K, X` есть линейная комбинация векторов циклов (строк матрицы циклов С). Таким образом, A (или K) и C определяют ортогональные подпространства, которые вместе образуют подпространство размерности m.
Используя материалы темы 6, K и C можно записать в виде K=(K1|I) C=(I|C2), где I – единичная матрица.
При выборе хорд стягивающего дерева в качестве первых m-n+1 столбцов. Разбивая таким же образом вектор токовых
переменных, получим: X=( |
X |
c |
) где Xc и Xb относятся к хордам |
|
|||
X |
|
||
|
b |
|
|
|
|
|
|
и ветвям дерева. |
|
|
|
Правило вершин означает, что KX(K1|I)( |
X |
c |
)=0 следова- |
|
|||
X |
|
||
|
b |
|
|
|
|
|
тельно
Xb=-K1Xc=CT2Xc, т.е. (X=CTXc) (1)
Таким образом, токи в ветвях выражаются через токи в хордах.
Аналогично, циклическое правило приводит к матричным
уравнениям CY=(±|C)( Yc )=0 Yc=-C2Yb=KT1Yb (Y=KTYb) (2)
Yb
80
Это уравнение выражает напряжение на хордах через напряжение на ветвях. Применение соотношений (1) и (2) составляет первый этап анализа.
Основные уравнения элементов удобно записать в матричной форме. Если напряжения заданны в виде явных функций от токов, то при этом получаем Y=ΩxX-Yg где Ωx- диагональная m×m матрица, i – диагональный элемент который является либо константой, либо дифференциальным или интегральным оператором; Yg – вектор столбец, элементы которого равны нулю, для позиций, соответствующих пассивным элементам и функциям g(t) для позиций, соответствующим источникам. Заметим, что соответствующие диагональные элементы Ωx равны нулю.
Если токи выражаются как явные функции напряжения, то получим
X= ΩyY-Xg |
(*) |
Предыдущее выражение, с учетом (1), может быть перепи- |
|
сано в виде : |
|
ΩxСTXc=Y+Yg |
|
Умножение обеих частей уравнения на C дает |
|
C ΩxCTXc=CY+CYg=CYg |
(3) |
В этом выражении неизвестными являются лишь токи в |
|
хордах. |
|
Выражение (*) может быть переписано |
|
ΩyKTYb=X+Xg |
|
и затем |
|
K ΩyKTYb=KX+KXg=KXg |
(4) |
где неизвестными являются только напряжения в ветвях. Уравнения (3) и (4) соответствуют формулировкам задачи
для циклов и вершин (узлов) соответственно. В случае, когда полученная система уравнений может быть решена известными математическими методами, оставшиеся неизвестными токи и напряжения легко находятся из приведенных выше соотношений.
В частности заметим, что KT и CT могут быть получены при визуальном анализе графа, после выбора дерева.
81
В случае, если некоторые элементы системы имеют более двух полюсов или если рассматриваются элементы согласования различных видов энергии в одной и той же системе, то матрица, характеризующая основные уравнения, имеет более сложную структуру и решение результирующей системы уравнений получается более сложным. Тем не менее, роль графа, представляющего систему, остается по существу той же самой.
82

15.СИГНАЛЬНЫЕ ГРАФЫ.
15.1.Общие представления о сигнальных графах.
Сигнальный граф – это направленный граф прохождения сигналов, графически изображающий систему уравнений которая описывает реальную физическую систему. В частности, в качестве такой системы может рассматриваться электрическая цепь. Вершинам сигнального графа соответствуют
1.неизвестные величины, входящие в физическую систему
2.величины, характеризующие внешнее воздействие на систему.
Дуги сигнального графа отображают причинноследственные связи между этими величинами. Указанные величины называются сигналами. Каждой дуге сигнального графа приписывается весовой коэффициент, который называется передачей дуги.
xi aij xj
Если дуга (i,j) имеет передачу ai,j, то
xj=aijxi где xi, xj – сигналы i-ой и j-ой вершин соответственно. Следовательно, при прохождении через дугу сигнал уменьшается на передачу дуги. Решая уравнение относительно xi полу-
чим xi=
x a
j ij
xi 1/aij xj
Т.е. сигнальный граф, соответствующий последнему уравнению отличается от предыдущего направлением передачи дуги. Таким образом, вид сигнального графа зависит от того, относительно какой из величин разрешено задание уравнения, т.е. от того, какая из величин рассматривается как причина, а какая как следствие.
Если в k вершине сходится несколько дуг, то значение сигнала в этой вершине будет равно сумме сигналов всех вхо-
83
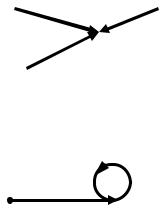
дящих в него вершин, т.е. xk=
Nk aik xk i 1
, где Nk – число дуг
направленных к k вершине. |
|
где aik – передача (i,k) дуги. |
|
x1 |
x2 |
|
xk |
xn
В число дуг, направленной к рассматриваемой вершине, могут входить дуги, начинающиеся в этой же вершине. Значение сигнала в вершине, имеющей петлю находиться по прави-
лу : xj=aijxi+aijxj
aij
xi |
aij |
xj |
т.е. при наличии петель, сигнал соответствующей вершины входит в левую и правую части уравнения.
Истоком сигнального графа является вершина от которой направлены все примыкающие к ней дуги. Вершина сигнального графа к которой направлены все примыкающие к ней дуги является стоком. Вершины, которые имеют входящие и исходящие дуги называются смешанными. Если сигнал, какойлибо вершины сигнального графа не выражается через сигналы других вершин, то такая вершина называется независимой. Если сигнал, какой-либо вершины сигнального графа выражается через сигналы других вершин, то такая вершина называется зависимой. К независимым относятся истоки, а к зависимым – стоки и смешанные вершины. Очевидно, уравнения передачи могут быть составлены только для зависимых вершин.
Передачей пути Pij называется произведение передач дуг, образующих путь между i и j вершинами. Произведение
84
передач всех дуг, входящих в контур L называется передачей контура Lj.
Дуги, исходящие из одной вершины и входящие в другую вершину, называются параллельными.
Два контура или контур и путь называются соприкасающимися, если они имеют общие вершины. В противном случае, они называются несоприкасающимися. Т.о. каждому сигнальному графу можно однозначно поставить в соответствие систему линейных алгебраических уравнений, составленных относительно сигналов зависимых вершин.
Для решения обратной задачи, т.е. построение сигнального графа, соответствующего заданной системе уравнений необходимо привести эту систему к причинно-следственной форме. Для этого каждое из входящих в систему уравнений должно быть разрешено относительно одной из переменных (различного для каждого из уравнения). Затем определяется общее число вершин N, которое равно сумме числа неизвестных переменных и числа ненулевых свободных членов уравнений. Построение графа начинается с нанесения точек, соответствующих вершинам. Затем вершины графа соединяются между собой дугами так, чтобы сумма сигналов все дуг, сходящихся в вершине, равнялись бы значению сигнала в этой вершине.
Обычно с целью повышения наглядности истоки располагают в левой части чертежа, стоки – в правой, а остальные вершины между ними. В каждой системе уравнений можно поставить в соответствие некоторые множества сигналов графов, которые называются равносильными.
15.2. Преобразования сигнальных графов.
После составления графа можно приступить к его решению, т.е. установить связь между двумя любыми его переменными. Существует два способа решения графа. Первый способ заключается в последовательном упрощении графа с помощью эквивалентных преобразований, в результате которых слож-
85

ный граф сводится к одной единственной дуге, передача которой равна передаче исходного графа.
По второму способу решения графа записывается сразу в виде формулы Мэзона. Второй способ более короткий, но менее наглядный. При первом способе наглядно проявляется роль отдельных параметров и связей. При этом устранение нежелательных связей и слабо влияющих параметров позволяет существенно упростить решение.
К эквивалентным преобразованиям графа относиться: 1. Объединение последовательных дуг
xi a xj b xk xi ab xk
86

2. Объединение параллельных дуг |
|
|
||||||
|
|
|
a |
|
|
|
|
|
xi |
|
|
|
xj |
xi |
|
a+b |
xj |
|
|
|
b |
|
|
|
|
|
|
3. Исключение петли в конце дуги |
|
||||||
|
|
|
|
b |
|
|
|
|
xi |
a |
|
xj |
|
|
xi |
|
a |
|
|
|
1 b |
|||||
|
|
|
|
|
|
|
||
|
4. Исключение контура в конце дуги |
|||||||
|
|
|
|
b |
|
|
|
|
|
xi a |
|
xj |
|
xk |
xi |
ab |
|
|
|
|
|
|
c |
|
|
|
|
4. |
Устранение промежуточной вершины |
||||||
|
|
|
|
|
x1 |
|
|
|
|
xi |
a |
xj |
b |
|
|
ab |
|
|
|
|
|
c |
x2 |
xi |
|
ac |
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
x3 |
|
|
ad |
x1 |
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
x |
|
ad |
x2 |
b |
|
x4 |
d |
x5 |
x2 |
bd |
|
|
c |
|
|
|
|
|
cd |
|
x3 |
|
|
|
|
|
x3 |
|
|
6. Инверсия дуги связанной с истоком
xj
xk b
x1 x2
x3
x5
87

x1 a
x3
x2 b
x1
|
b |
|
a |
||
|
x2
1 a
x3
|
|
7. Расщепление вершины |
|
|
|
|
|||
x1 |
|
a |
c |
x4 |
x1 |
a |
c |
x4 |
|
|
|
x3 |
d |
x5 |
|
|
|
|
|
|
|
x5 |
|
|
|
|
|
d |
x5 |
|
|
b |
|
|
|
b |
|
e |
|
x2 |
|
|
e |
x6 |
|
x2 |
|
|
x6 |
|
|
8. Удаление вершины |
|
|
|
|
|
||
x1 |
a |
x2 |
|
x1 |
a |
x2 |
1 |
x`2 |
|
15.3. Формула Мэзона.
Она позволяет вычислить передачу сигнального графа непосредственно по его структуре не прибегая к его преобразованиям. Для графа с одним источником формула Мэзона
имеет вид K= |
1 |
Pk k где Pk – передачи k-го пути от источ- |
|
|
|||
|
|
||
ника до стока; |
k – определитель части графа не касающегося |
||
k-го пути; – определитель графа.
Если граф имеет m контуров (петель), то определитель
графа
=1- L1 L2 L3 ...
88
где |
L1 - сумма передач всех m-контуров |
|
|
L2 |
- сумма произведений передач двух любых конту- |
ров, не |
касающихся друг друга |
|
|
L3 |
- сумма произведений передач трех любых конту- |
ров, не |
касающихся друг друга |
|
|
Определитель k находят с помощью выражения |
|
|
|
k=1- L1k L2k L3k ... |
где |
L1k |
- сумма передач всех контуров (петель), не каса- |
ющихся k-го пути
L2k
- сумма произведений передач двух любых кон-
туров, не касающихся друг друга и k-го пути и т.д. Определитель графа не зависит от возможных путей в
графе. Определитель k можно найти из выражения для , исключив из него члены, которые содержат контуры, касающегося данного прямого пути. Формулы Мэзона можно использовать в графе, содержащем несколько источников. Для этого формулу Мэзона применяют к каждому источнику в отдельности, а результат суммируют.
При составлении графа цепи, содержащей активные элементы, вначале строятся графы всех активных элементов этой цепи, а затем эти графы связываются уравнениями пассивной части цепи, выполняя условия причинно-следственной связи.
89
