- •Введение
- •1. Правила выполнения курсовой работы
- •Принятые обозначения
- •2. Правила сдачи курсовой работы
- •3. Правила оформления курсовой работы
- •4. Задания на курсовую работу Задание 1. Определение реакций связей составных конструкций
- •Задание 2. Кинематический анализ многозвенного механизма
- •Задание 3. Исследование движения механических систем с помощью теоремы об изменении кинетической энергии системы
- •Задание 4. Исследование движения механических систем с помощью методов аналитической механики
- •Задание 5 (дополнительное). Определение сил реакций составной конструкции с помощью принципа возможных перемещений (пвп)
- •Приложение а
- •Форма титульного листа курсовой работы
- •Расчетно-пояснительная записка
- •201__ Приложение б
- •Форма бланка задания на курсовую работу
- •Приложение в
- •Пример оформления содержания
- •Приложение г
- •Примеры библиографических описаний
- •Приложение д
- •Статика Силы реакции связей
- •Распределенные силы
- •Алгебраический момент силы относительно точки
- •Теорема Вариньона для плоской системы сил
- •Условия равновесия плоской системы сил
- •Составная конструкция (сочлененная система тел)
- •Приложение е
- •Кинематика
- •Поступательное движение твердого тела
- •Вращение твердого тела вокруг неподвижной оси
- •Плоское (плоскопараллельное) движение твердого тела
- •Теорема о проекциях скоростей
- •Приложение ж
- •Динамика Работа силы
- •Примеры вычисления работы силы
- •Кинетическая энергия
- •Теорема об изменении кинетической энергии системы
- •Приложение и
- •Аналитическая механика Возможные перемещения
- •Элементарная работа силы на возможном перемещении. Идеальные связи
- •Принцип возможных перемещений (принцип Лагранжа)
- •Обобщенные координаты системы
- •Обобщенные силы
- •Вычисление обобщенной силы
- •Общее уравнение динамики (принцип Даламбера-Лагранжа)
- •Уравнения Лагранжа второго рода
- •Заключение
- •Контрольные вопросы и дополнительные задания Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Библиографический список
- •Оглавление
- •394026 Воронеж, Московский просп., 14
Задание 2. Кинематический анализ многозвенного механизма
Плоский
механизм состоит из стержней 1, 2, 3, 4 и
ползуна
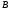 или
или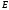 (рис. 2.0–2.7) или из стержней 1, 2, 3 и ползунов
(рис. 2.0–2.7) или из стержней 1, 2, 3 и ползунов или
или (рис. 2.8, 2.9), соединенных друг с другом и
с неподвижными опорами
(рис. 2.8, 2.9), соединенных друг с другом и
с неподвижными опорами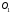 ,
,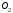 шарнирами. Точка
шарнирами. Точка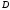 находится в середине стержня
находится в середине стержня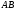 .
Длины стержней равны соответственно
.
Длины стержней равны соответственно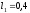 м,
м, м,
м,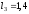 м,
м,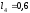 м. Положение механизма определяется
углами
м. Положение механизма определяется
углами .
Значения этих углов и других заданных
величин указаны в табл. 3 (для рис. 2.0–2.4)
или в табл. 4 (для рис. 2.5–2.9). При этом в
табл. 3
.
Значения этих углов и других заданных
величин указаны в табл. 3 (для рис. 2.0–2.4)
или в табл. 4 (для рис. 2.5–2.9). При этом в
табл. 3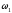 и
и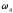 – величины постоянные.
– величины постоянные.
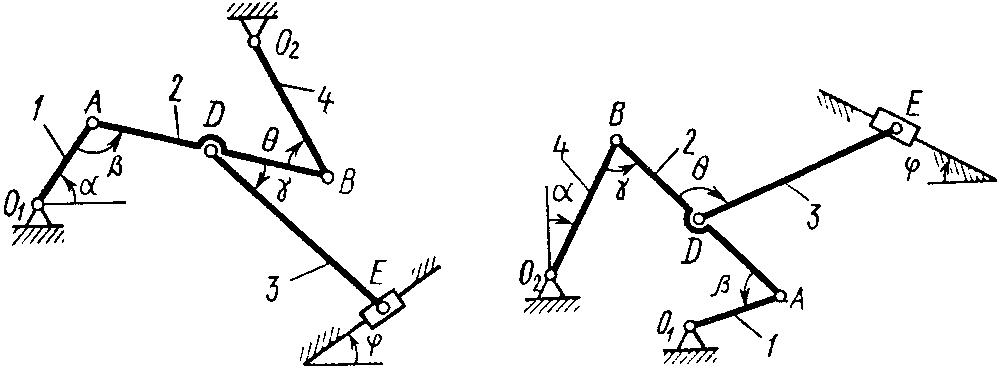
Рис. 2.0 Рис. 2.1

Рис. 2.2 Рис. 2.3
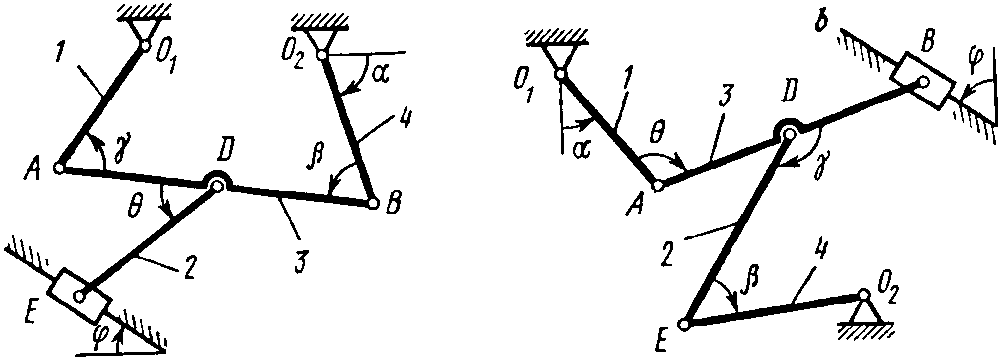
Рис. 2.4 Рис. 2.5

Рис. 2.6 Рис. 2.7
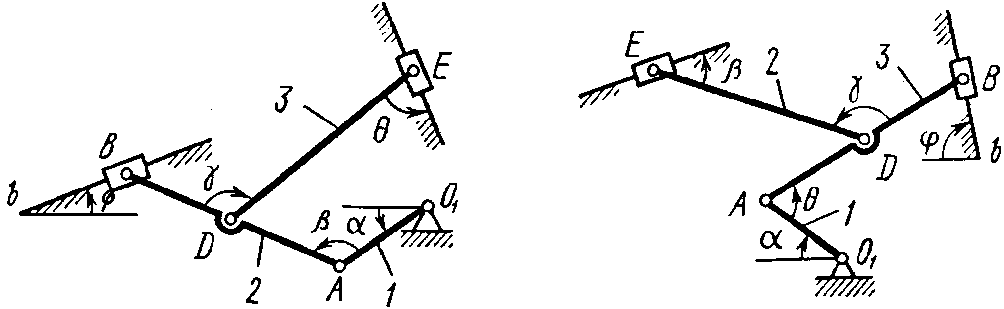
Рис. 2.8 Рис. 2.9
Дуговые
стрелки на рисунках показывают, как при
построении чертежа механизма должны
откладываться соответствующие углы:
по ходу или против хода часовой стрелки
(например, угол
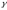 на рис. 2.8 отложить от
на рис. 2.8 отложить от по ходу часовой стрелки, а на рис. 2.9 –
против хода часовой стрелки).
по ходу часовой стрелки, а на рис. 2.9 –
против хода часовой стрелки).
Таблица 3
|
№ условия |
Углы, град |
Дано |
Найти | |||||||||
|
|
|
|
|
|
ω1, 1/с |
ω4, 1/с |
v точек |
ω звена |
а точки | |||
|
0 |
0 |
60 |
30 |
0 |
120 |
6 |
– |
В, Е |
DЕ |
B | ||
|
1 |
90 |
120 |
150 |
0 |
30 |
– |
4 |
А, Е |
AB |
A | ||
|
2 |
30 |
60 |
30 |
0 |
120 |
5 |
– |
В, Е |
AB |
B | ||
|
3 |
60 |
150 |
150 |
90 |
30 |
– |
5 |
А, Е |
DЕ |
A | ||
|
4 |
30 |
30 |
60 |
0 |
150 |
4 |
– |
D, Е |
AB |
B | ||
|
5 |
90 |
120 |
120 |
90 |
60 |
– |
6 |
А, Е |
AB |
A | ||
|
6 |
90 |
150 |
120 |
90 |
30 |
3 |
– |
В, Е |
DЕ |
B | ||
|
7 |
0 |
60 |
60 |
0 |
120 |
– |
2 |
А, Е |
DЕ |
A | ||
|
8 |
60 |
150 |
120 |
90 |
30 |
2 |
– |
D, Е |
AB |
B | ||
|
9 |
30 |
120 |
150 |
0 |
60 |
– |
8 |
А, Е |
DЕ |
A | ||
Таблица 4
|
№ условия |
Углы, град |
Дано |
Найти | |||||||||
|
|
|
|
|
|
ω1, 1/с |
ε1, 1/с2 |
vB, м/с |
aB, м/с2 |
v точек |
ω звена |
а точки | |
|
0 |
120 |
30 |
30 |
90 |
150 |
2 |
4 |
– |
– |
В, Е |
AB |
B |
|
1 |
0 |
60 |
90 |
0 |
120 |
– |
– |
4 |
6 |
А, Е |
DЕ |
A |
|
2 |
60 |
150 |
30 |
90 |
30 |
3 |
5 |
– |
– |
В, Е |
AB |
B |
|
3 |
0 |
150 |
30 |
0 |
60 |
– |
– |
6 |
8 |
А, Е |
AB |
A |
|
4 |
30 |
120 |
120 |
0 |
60 |
4 |
6 |
– |
– |
D, Е |
DЕ |
B |
|
5 |
90 |
120 |
90 |
90 |
60 |
– |
– |
8 |
10 |
D, Е |
DЕ |
A |
|
6 |
0 |
150 |
90 |
0 |
120 |
5 |
8 |
– |
– |
В, Е |
DЕ |
B |
|
7 |
30 |
120 |
30 |
0 |
60 |
– |
– |
2 |
5 |
А, Е |
AB |
A |
|
8 |
90 |
120 |
120 |
90 |
150 |
6 |
10 |
– |
– |
В, Е |
DЕ |
B |
|
9 |
60 |
60 |
60 |
90 |
30 |
– |
– |
5 |
4 |
D, Е |
AB |
A |
Определить
 звена
звена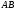 и величины, указанные в таблицах в
столбцах «Найти».
и величины, указанные в таблицах в
столбцах «Найти».
Построение
чертежа начинать со стержня, направление
которого определяется углом
 ;
ползун с направляющими для большей
наглядности изобразить так, как в примере
2 (см. рис. 2.10).
;
ползун с направляющими для большей
наглядности изобразить так, как в примере
2 (см. рис. 2.10).
Заданные
угловую скорость и угловое ускорение
считать направленными против часовой
стрелки, а заданные скорость
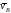 и ускорение
и ускорение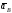 – от точки
– от точки к
к (на рис. 2.5–2.9).
(на рис. 2.5–2.9).
Указания. Задание 2 – на исследование плоскопараллельного движения твердого тела (см. приложение Е). При ее решении для определения скоростей точек механизма и угловых скоростей его звеньев следует воспользоваться теоремой о проекциях скоростей двух точек тела и понятием о мгновенном центре скоростей, применяя эту теорему (или это понятие) к каждому звену механизма в отдельности.
При
определении ускорений точек механизма
исходить из векторного равенства
 ,
где
,
где – точка, ускорение
– точка, ускорение которой или задано, или непосредственно
определяется по условиям задачи (если
точка
которой или задано, или непосредственно
определяется по условиям задачи (если
точка движется по дуге окружности, то
движется по дуге окружности, то );
);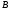 – точка, ускорение
– точка, ускорение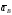 которой нужно определить (в случае,
когда точка
которой нужно определить (в случае,
когда точка движется по дуге окружности, см.
«Примечание»
в конце приведенного ниже примера 2).
движется по дуге окружности, см.
«Примечание»
в конце приведенного ниже примера 2).
Пример 2
Механизм
(рис. 2.10, а) состоит из стержней 1, 2, 3, 4 и
ползуна
 ,
соединенных друг с другом и с неподвижными
опорами
,
соединенных друг с другом и с неподвижными
опорами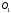 и
и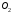 шарнирами.
шарнирами.
Дано:
 ,
, ,
,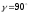 ,
, ,
,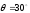 ,
,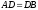 ,
,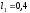 м,
м, м,
м,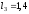 м,
м, с-1,
с-1,
 с-2
(направления
с-2
(направления
 и
и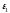 – против хода часовой стрелки).
– против хода часовой стрелки).
Определить:
 ,
, ,
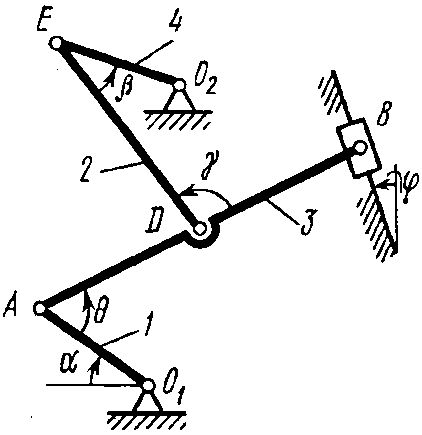
,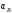 ,
, ,
, .
.
Решение:
1. Строим положение механизма в соответствии с заданными углами и выбранным масштабом длин (рис. 2.10, б; на этом рисунке изображаем все векторы скоростей).
2.
Определяем
 .
Точка
.
Точка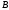 принадлежит стержню
принадлежит стержню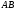 .
Чтобы найти
.
Чтобы найти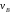 ,
надо знать скорость какой-нибудь другой
точки этого стержня и направление
,
надо знать скорость какой-нибудь другой
точки этого стержня и направление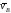 .
По данным задачи, учитывая направление
.
По данным задачи, учитывая направление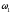 ,
можем определить
,
можем определить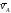 .
Численно:
.
Численно:
Рис. 2.10, а
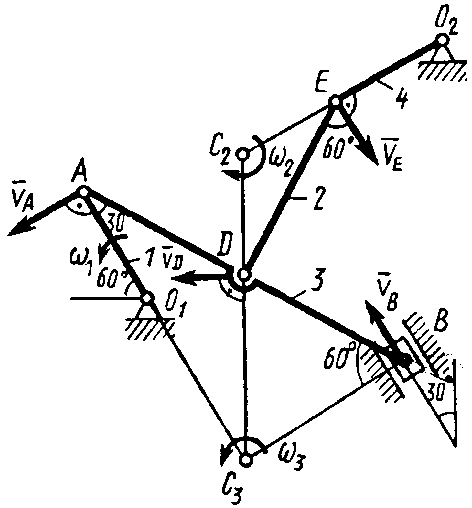
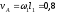 м/с,
м/с,
 . (1)
. (1)
Направление
 найдем, учтя, что точка
найдем, учтя, что точка принадлежит одновременно ползуну,
движущемуся вдоль направляющих
поступательно. Теперь, зная
принадлежит одновременно ползуну,
движущемуся вдоль направляющих
поступательно. Теперь, зная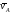 и направление
и направление ,
воспользуемся теоремой о проекциях
скоростей двух точек тела (стержня
,
воспользуемся теоремой о проекциях
скоростей двух точек тела (стержня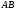 )
на прямую, соединяющую эти точки (прямая
)
на прямую, соединяющую эти точки (прямая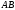 ).
Сначала по этой теореме устанавливаем,
в какую сторону направлен вектор
).
Сначала по этой теореме устанавливаем,
в какую сторону направлен вектор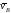 (проекции скоростей должны иметь
одинаковые знаки). Затем, вычисляя эти
проекции, находим
(проекции скоростей должны иметь
одинаковые знаки). Затем, вычисляя эти
проекции, находим
Рис. 2.10, б
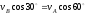 ,
,
 м/с. (2)
м/с. (2)
3.
Определяем
 .
Точка
.
Точка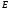 принадлежит стержню
принадлежит стержню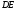 .
Следовательно, по аналогии с предыдущим,
чтобы определить
.
Следовательно, по аналогии с предыдущим,
чтобы определить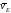 ,
надо сначала найти скорость точки
,
надо сначала найти скорость точки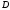 ,
принадлежащей одновременно стержню
,
принадлежащей одновременно стержню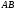 .
Для этого, зная
.
Для этого, зная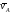 и
и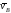 ,
строим мгновенный центр скоростей (МЦС)
стержня
,
строим мгновенный центр скоростей (МЦС)
стержня .
Это точка
.
Это точка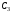 ,
лежащая на пересечении перпендикуляров
к
,
лежащая на пересечении перпендикуляров
к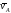 и
и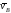 ,
восставленных из точек
,
восставленных из точек и
и (к
(к перпендикулярен стержень 1). По направлению
вектора
перпендикулярен стержень 1). По направлению
вектора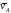 определяем направление поворота стержня
определяем направление поворота стержня вокруг МЦС
вокруг МЦС .
Вектор
.
Вектор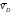 перпендикулярен отрезку
перпендикулярен отрезку ,
соединяющему точки
,
соединяющему точки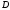 и
и ,
и направлен в сторону поворота. Величину
,
и направлен в сторону поворота. Величину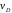 найдем из пропорции:
найдем из пропорции:
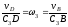 . (3)
. (3)
Чтобы
вычислить
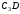 и
и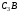 ,
заметим, что
,
заметим, что – прямоугольный, так как острые углы в
нем равны 30° и 60°, и что
– прямоугольный, так как острые углы в
нем равны 30° и 60°, и что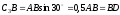 .
Тогда
.
Тогда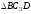 является равносторонним и
является равносторонним и .
В результате равенство (3) дает
.
В результате равенство (3) дает
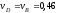 м/с,
м/с,
 . (4)
. (4)
Так
как точка
 принадлежит одновременно стержню
принадлежит одновременно стержню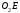 ,
вращающемуся вокруг
,
вращающемуся вокруг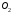 ,
то
,
то .
Тогда, восставляя из точек
.
Тогда, восставляя из точек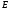 и
и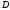 перпендикуляры к скоростям
перпендикуляры к скоростям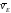 и
и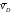 ,
построим МЦС
,
построим МЦС стержня
стержня .
По направлению вектора
.
По направлению вектора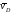 определяем направление поворота стержня
определяем направление поворота стержня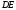 вокруг центра
вокруг центра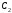 .
Вектор
.
Вектор направлен в сторону поворота этого
стержня. Из рис. 2.10,б видно, что
направлен в сторону поворота этого
стержня. Из рис. 2.10,б видно, что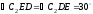 ,
откуда
,
откуда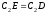 .
Составив теперь пропорцию, найдем, что
.
Составив теперь пропорцию, найдем, что
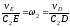 ,
,
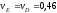 м/с. (5)
м/с. (5)
4.
Определяем
 .
Так как МЦС стержня 2 известен (точка
.
Так как МЦС стержня 2 известен (точка )
и
)
и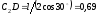 м, то
м, то
 с–1. (6)
с–1. (6)
5.
Определяем
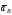 (рис. 2.10, в, на котором изображаем все
векторы ускорений). Точка
(рис. 2.10, в, на котором изображаем все
векторы ускорений). Точка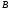 принадлежит стержню
принадлежит стержню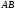 .
Чтобы найти
.
Чтобы найти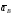 ,
надо знать ускорение какой-нибудь другой
точки стержня
,
надо знать ускорение какой-нибудь другой
точки стержня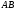 и траекторию точки
и траекторию точки .
По данным задачи можем определить
.
По данным задачи можем определить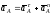 ,
где численно
,
где численно
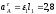 м/с2,
м/с2,
Рис. 2.10, в
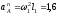 м/с2.
(7)
м/с2.
(7)
Вектор
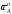 направлен вдоль
направлен вдоль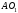 ,
а
,
а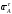 – перпендикулярно
– перпендикулярно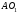 .
Изображаем эти векторы на чертеже (см.
рис. 2.10, в). Так как точка
.
Изображаем эти векторы на чертеже (см.
рис. 2.10, в). Так как точка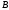 одновременно принадлежит ползуну, то
вектор
одновременно принадлежит ползуну, то
вектор параллелен направляющим ползуна.
Изображаем вектор
параллелен направляющим ползуна.
Изображаем вектор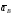 на чертеже, полагая, что он направлен в
ту же сторону, что и
на чертеже, полагая, что он направлен в
ту же сторону, что и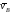 .
.
Для
определения
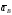 воспользуемся равенством
воспользуемся равенством
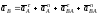 . (8)
. (8)
Изображаем
на чертеже векторы
 (вдоль
(вдоль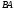 от
от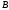 к
к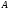 )
и
)
и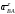 (в любую сторону перпендикулярно
(в любую сторону перпендикулярно ).
Численно
).
Численно Найдя
Найдя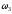 с помощью построенного МЦС
с помощью построенного МЦС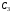 стержня 3, получим
стержня 3, получим
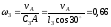 с–1,
с–1,
 м/с2.
(9)
м/с2.
(9)
Таким
образом, у величин, входящих в равенство
(8), неизвестны только числовые значения
 и
и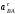 .
Их можно найти, спроектировав обе части
равенства (8) на две оси.
.
Их можно найти, спроектировав обе части
равенства (8) на две оси.
Чтобы
определить
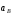 ,
спроектируем обе части равенства (8) на
направление
,
спроектируем обе части равенства (8) на
направление (ось
(ось ).
Тогда получим
).
Тогда получим
 . (10)
. (10)
Подставив в равенство (10) числовые значения всех величин из (7) и (9), найдем, что
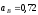 м/с2. (11)
м/с2. (11)
Так
как получилось
 ,
то, следовательно, вектор
,
то, следовательно, вектор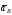 направлен как показано на рис. 2.10, в.
направлен как показано на рис. 2.10, в.
6.
Определяем
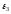 .
Чтобы найти
.
Чтобы найти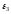 ,
сначала определим
,
сначала определим .
Для этого обе части равенства (8)
спроектируем на направление,
перпендикулярное
.
Для этого обе части равенства (8)
спроектируем на направление,
перпендикулярное (ось
(ось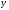 ).
Тогда получим:
).
Тогда получим:
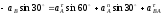 . (12)
. (12)
Подставив
в равенство (12) числовые значения всех
величин из (11) и (7), найдем, что
![]() м/с2.
Знак минус указывает, что направление
м/с2.
Знак минус указывает, что направление
 противоположно показанному на рис.
2.10, в. Теперь из равенства
противоположно показанному на рис.
2.10, в. Теперь из равенства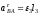 получим:
получим:
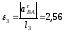 с–2.
с–2.
Ответ:
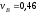 м/с,
м/с, м/с,
м/с,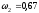 с–1,
с–1,
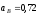 м/с2,
м/с2,
 с–2.
с–2.
Примечание.
Если точка
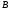 ,
ускорение которой определяется, движется
не прямолинейно (например, как на рис.
2.0–2.4, где
,
ускорение которой определяется, движется
не прямолинейно (например, как на рис.
2.0–2.4, где движется по окружности радиуса
движется по окружности радиуса ),
то направление
),
то направление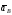 заранее неизвестно.
заранее неизвестно.
В
этом случае
 также следует представить двумя
составляющими (
также следует представить двумя
составляющими ( )
и исходное уравнение (8) примет вид
)
и исходное уравнение (8) примет вид
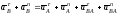 . (13)
. (13)
При
этом вектор
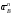 (см., например, рис. 2.0) будет направлен
вдоль
(см., например, рис. 2.0) будет направлен
вдоль ,
а вектор
,
а вектор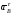 – перпендикулярно
– перпендикулярно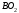 в любую сторону. Числовые значения
в любую сторону. Числовые значения ,
,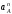 и
и определяются так же, как в рассмотренном
примере (в частности, по условиям задачи
может быть
определяются так же, как в рассмотренном
примере (в частности, по условиям задачи
может быть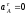 или
или ,
если точка
,
если точка движется прямолинейно).
движется прямолинейно).
Значение
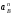 также вычисляется по формуле
также вычисляется по формуле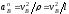 ,
где
,
где — радиус окружности
— радиус окружности ,
а
,
а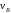 определяется так же, как скорость любой
другой точки механизма.
определяется так же, как скорость любой
другой точки механизма.
После
этого в равенстве (13) остаются неизвестными
только значения
 и
и ,
и они, как и в рассмотренном примере,
находятся проектированием обеих частей
равенства (13) на две оси.
,
и они, как и в рассмотренном примере,
находятся проектированием обеих частей
равенства (13) на две оси.
Найдя
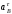 ,
можем вычислить искомое ускорение
,
можем вычислить искомое ускорение .
Величина
.
Величина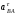 служит для нахождения
служит для нахождения (как в рассмотренном примере).
(как в рассмотренном примере).