
- •Введение
- •1. Правила выполнения курсовой работы
- •Принятые обозначения
- •2. Правила сдачи курсовой работы
- •3. Правила оформления курсовой работы
- •4. Задания на курсовую работу Задание 1. Определение реакций связей составных конструкций
- •Задание 2. Кинематический анализ многозвенного механизма
- •Задание 3. Исследование движения механических систем с помощью теоремы об изменении кинетической энергии системы
- •Задание 4. Исследование движения механических систем с помощью методов аналитической механики
- •Задание 5 (дополнительное). Определение сил реакций составной конструкции с помощью принципа возможных перемещений (пвп)
- •Приложение а
- •Форма титульного листа курсовой работы
- •Расчетно-пояснительная записка
- •201__ Приложение б
- •Форма бланка задания на курсовую работу
- •Приложение в
- •Пример оформления содержания
- •Приложение г
- •Примеры библиографических описаний
- •Приложение д
- •Статика Силы реакции связей
- •Распределенные силы
- •Алгебраический момент силы относительно точки
- •Теорема Вариньона для плоской системы сил
- •Условия равновесия плоской системы сил
- •Составная конструкция (сочлененная система тел)
- •Приложение е
- •Кинематика
- •Поступательное движение твердого тела
- •Вращение твердого тела вокруг неподвижной оси
- •Плоское (плоскопараллельное) движение твердого тела
- •Теорема о проекциях скоростей
- •Приложение ж
- •Динамика Работа силы
- •Примеры вычисления работы силы
- •Кинетическая энергия
- •Теорема об изменении кинетической энергии системы
- •Приложение и
- •Аналитическая механика Возможные перемещения
- •Элементарная работа силы на возможном перемещении. Идеальные связи
- •Принцип возможных перемещений (принцип Лагранжа)
- •Обобщенные координаты системы
- •Обобщенные силы
- •Вычисление обобщенной силы
- •Общее уравнение динамики (принцип Даламбера-Лагранжа)
- •Уравнения Лагранжа второго рода
- •Заключение
- •Контрольные вопросы и дополнительные задания Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Библиографический список
- •Оглавление
- •394026 Воронеж, Московский просп., 14
4. Задания на курсовую работу Задание 1. Определение реакций связей составных конструкций
Конструкция
состоит из жесткого угольника и стержня,
которые в точке
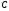 или соединены друг с другом шарнирно
(рис. 1.0–1.5), или свободно опираются друг
о друга (рис. 1.6–1.9).
или соединены друг с другом шарнирно
(рис. 1.0–1.5), или свободно опираются друг
о друга (рис. 1.6–1.9).

Рис. 1.0 Рис. 1.1
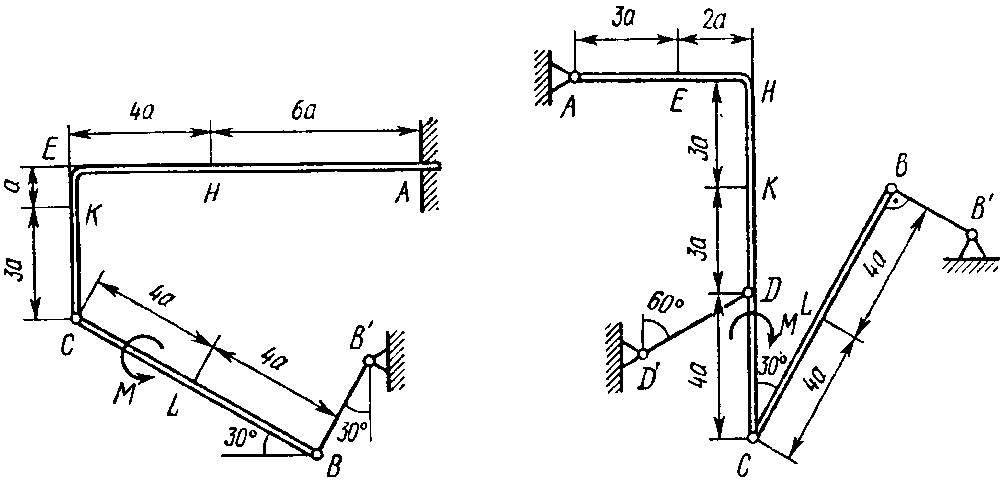
Рис. 1.2 Рис. 1.3
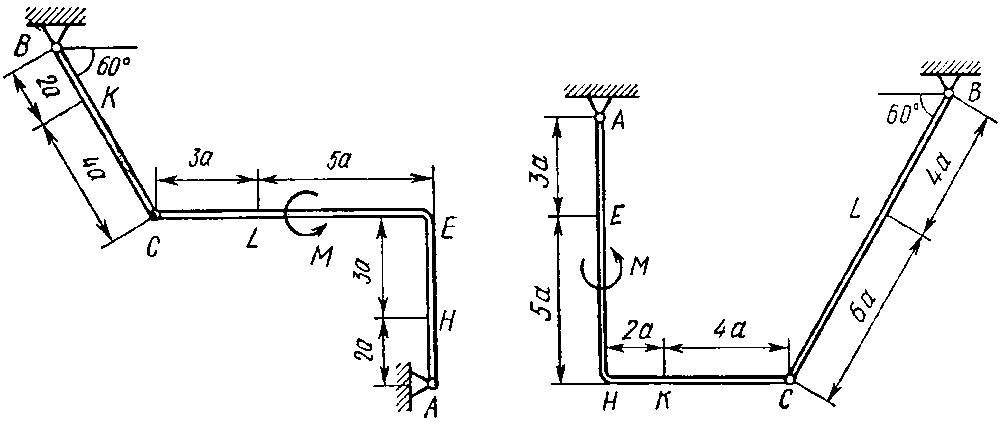
Рис. 1.4 Рис. 1.5
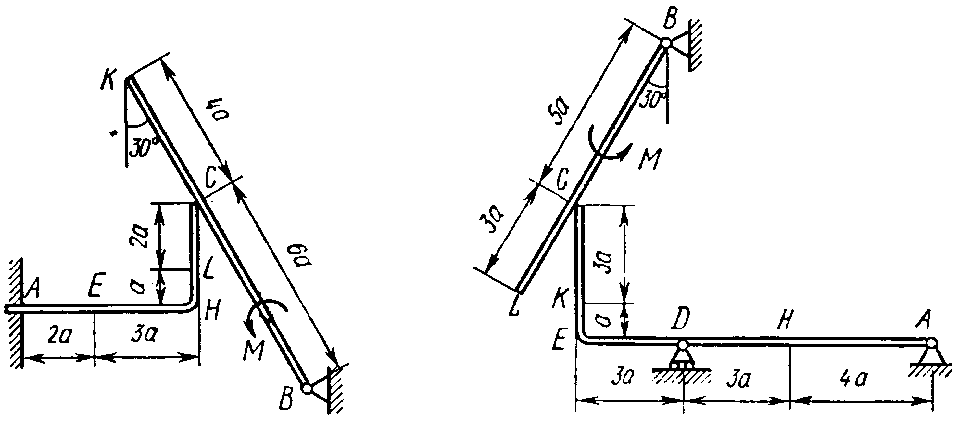
Рис. 1.6 Рис. 1.7
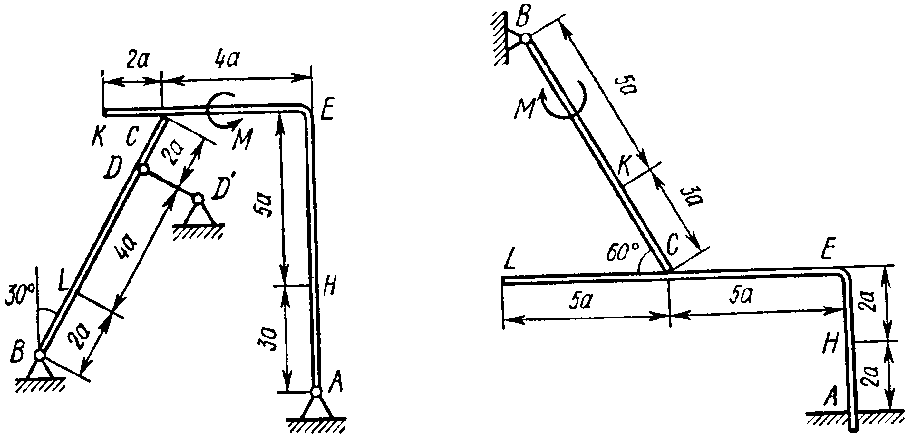
Рис. 1.8 Рис. 1.9
Внешними
связями, наложенными на конструкцию,
являются в точке
 или шарнир, или жесткая заделка; в точке
или шарнир, или жесткая заделка; в точке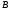 или гладкая плоскость (рис. 1.0 и 1.1), или
невесомый стержень
или гладкая плоскость (рис. 1.0 и 1.1), или
невесомый стержень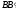 (рис. 1.2 и 1.3), или шарнир (рис. 1.4–1.9); в
точке
(рис. 1.2 и 1.3), или шарнир (рис. 1.4–1.9); в
точке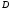 или невесомый стержень
или невесомый стержень (рис. 1.0, 1.3, 1.8), или шарнирная опора на
катках (рис. 1.7).
(рис. 1.0, 1.3, 1.8), или шарнирная опора на
катках (рис. 1.7).
На
каждую конструкцию действуют: пара сил
с моментом
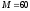
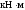 ,
равномерно распределенная нагрузка
интенсивности
,
равномерно распределенная нагрузка
интенсивности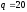
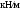 и еще две силы. Эти силы, их направления
и точки приложения указаны в табл. 1; там
же в столбце «Нагруженный участок»
указано, на каком участке действует
распределенная нагрузка (например, в
условиях № 1 на конструкцию действуют
сила
и еще две силы. Эти силы, их направления
и точки приложения указаны в табл. 1; там
же в столбце «Нагруженный участок»
указано, на каком участке действует
распределенная нагрузка (например, в
условиях № 1 на конструкцию действуют
сила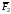 под углом 60° к горизонтальной оси,
приложенная в точке
под углом 60° к горизонтальной оси,
приложенная в точке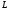 ,
сила
,
сила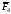 под углом 30° к горизонтальной оси,
приложенная в точке
под углом 30° к горизонтальной оси,
приложенная в точке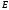 ,
и нагрузка, распределенная на участке
,
и нагрузка, распределенная на участке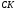 ).
).
Определить
реакции связей в точках
 ,
, ,
,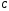 (для рис. 1.0, 1.3, 1.7, 1.8 еще и в точке
(для рис. 1.0, 1.3, 1.7, 1.8 еще и в точке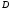 ),
вызванные заданными нагрузками. При
окончательных расчетах принять
),
вызванные заданными нагрузками. При
окончательных расчетах принять м. Направление распределенной нагрузки
на различных по расположению участках
указано в табл. 2
м. Направление распределенной нагрузки
на различных по расположению участках
указано в табл. 2
Указания. Задание 1 – на равновесие системы тел, находящихся под действием плоской системы сил (см. приложение Д). При ее решении можно или рассмотреть сначала равновесие всей системы в целом, а затем равновесие одного из тел системы, изобразив его отдельно, или же сразу расчленить систему и рассмотреть равновесие каждого из тел в отдельности, учтя при этом закон о равенстве действия и противодействия. В задачах, где имеется жесткая заделка, учесть, что ее реакция представляется силой, модуль и направление которой неизвестны, и парой сил, момент которой тоже неизвестен.
Таблица 1
|
Сила |
|
|
|
|
Нагруженный участок | ||||
|
|
|
|
| ||||||
|
№ условия |
Точка приложения |
α, град |
Точка приложения |
α, град |
Точка приложения |
α, град |
Точка приложения |
α, град | |
|
0 |
K |
60 |
– |
– |
H |
30 |
– |
– |
CL |
|
1 |
– |
– |
L |
60 |
– |
– |
E |
30 |
CK |
|
2 |
L |
15 |
– |
– |
K |
60 |
– |
– |
AE |
|
3 |
– |
– |
K |
30 |
– |
– |
H |
60 |
CL |
|
4 |
L |
30 |
– |
– |
E |
60 |
– |
– |
CK |
|
5 |
– |
– |
L |
75 |
– |
– |
K |
30 |
AE |
|
6 |
E |
60 |
– |
– |
K |
75 |
– |
– |
CL |
|
7 |
– |
– |
H |
60 |
L |
30 |
– |
– |
CK |
|
8 |
– |
– |
K |
30 |
– |
– |
E |
15 |
CL |
|
9 |
H |
30 |
– |
– |
– |
– |
L |
60 |
CK |
Таблица 2
|
Участок на угольнике |
Участок на стержне | ||
|
горизонтальный |
вертикальный |
рис. С1.0, С1.3, С1.5, С1.7, С1.8 |
рис. С1.1, С1.2, С1.4, С1.6, С1.9 |
|
|
|
|
|
Пример 1
На
угольник
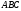 (
(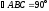 ),
конец
),
конец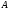 которого жестко заделан, в точке
которого жестко заделан, в точке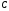 опирается стержень
опирается стержень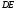 (рис. 1.10, а). Стержень имеет в точке
(рис. 1.10, а). Стержень имеет в точке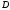 неподвижную шарнирную опору и к нему
приложена сила
неподвижную шарнирную опору и к нему
приложена сила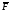 ,
а к угольнику – равномерно распределенная
на участке
,
а к угольнику – равномерно распределенная
на участке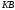 нагрузка интенсивности
нагрузка интенсивности и пара с моментом
и пара с моментом .
.
Дано:
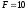 кН,
кН,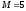
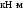 ,
,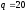
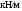 ,
,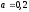 м.
м.
Определить:
реакции в точках
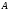 ,
,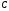 ,
,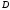 .
.
Решение:
1.
Для определения реакций расчленим
систему и рассмотрим сначала равновесие
стержня
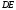 (рис. 1.10, б). Проведем координатные оси
(рис. 1.10, б). Проведем координатные оси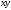 и изобразим действующие на стержень
силы: силу
и изобразим действующие на стержень
силы: силу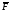 ,
реакцию
,
реакцию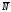 ,
направленную перпендикулярно стержню,
и составляющие
,
направленную перпендикулярно стержню,
и составляющие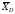 и
и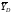 реакции шарнира
реакции шарнира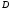 .
Для полученной плоской системы сил
составляем три уравнения равновесия:
.
Для полученной плоской системы сил
составляем три уравнения равновесия:
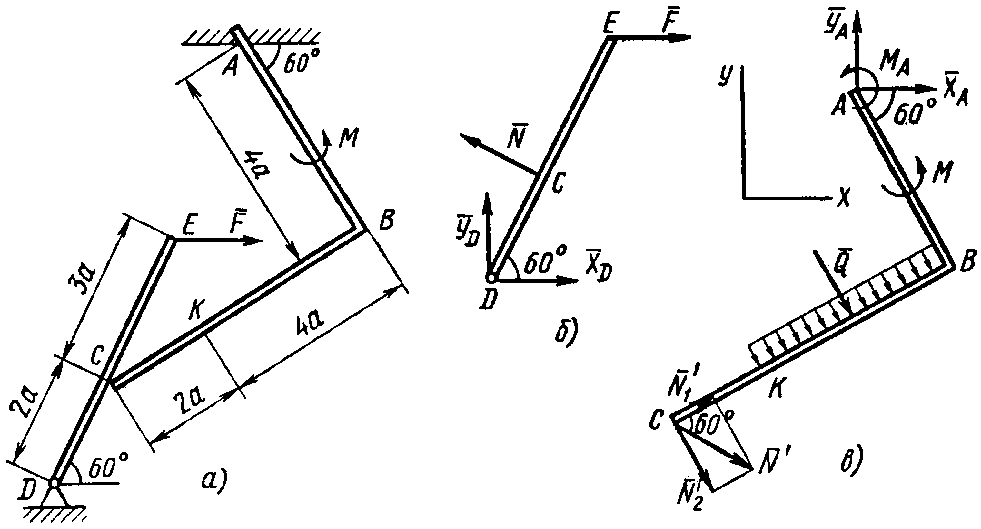
Рис. 1.10
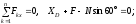 (1)
(1)
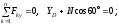 (2)
(2)
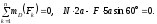 (3)
(3)
2.
Рассмотрим равновесие угольника (рис.
1.10, в). На него действуют сила давления
стержня
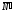 ,
направленная противоположно реакции
,
направленная противоположно реакции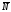 ,
равномерно распределенная нагрузка,
которую заменяем силой
,
равномерно распределенная нагрузка,
которую заменяем силой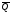 ,
приложенной в середине участка
,
приложенной в середине участка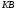 (
(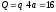 кН), пара сил с моментом
кН), пара сил с моментом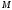 и реакция жесткой заделки, слагающаяся
из силы, которую представим составляющими
и реакция жесткой заделки, слагающаяся
из силы, которую представим составляющими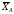 и
и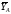 ,
и моментом
,
и моментом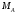 .
Для этой плоской системы сил составляем
уравнения равновесия:
.
Для этой плоской системы сил составляем
уравнения равновесия:
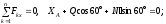 (4)
(4)
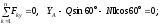 (5)
(5)

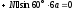 . (6)
. (6)
При
вычислении момента силы
 разлагаем ее на составляющие
разлагаем ее на составляющие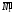 и
и и применяем теорему Вариньона. Подставив
в составленные уравнения числовые
значения заданных величин и решив
систему уравнений (1)–(6), найдем искомые
реакции. При решении учитываем, что
численно
и применяем теорему Вариньона. Подставив
в составленные уравнения числовые
значения заданных величин и решив
систему уравнений (1)–(6), найдем искомые
реакции. При решении учитываем, что
численно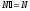 в силу равенства действия и противодействия.
в силу равенства действия и противодействия.
Ответ:
 кН,
кН, кН,
кН,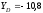 кН,
кН,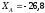 кН,
кН,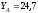 кН,
кН,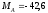
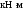 .
Знаки минус указывают, что силы
.
Знаки минус указывают, что силы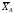 ,
,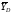 и момент
и момент направлены противоположно показанным
на рисунках.
направлены противоположно показанным
на рисунках.


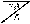

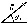
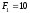 кН
кН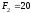 кН
кН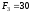 кН
кН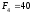 кН
кН


