Обобщенные координаты системы

Пусть система состоит из 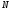точек и, следовательно, ее положение в пространстве в каждый момент времени определяется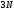координатами точек системы, например декартовыми.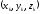

Предположим, что на систему наложены голономные связи, уравнения которых в общем случае могут содержать и производные от координат точек, но после их интегрирования они свелись к геометрическим и имеют форму

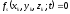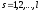, . (ПИ.4)

Освобождающие связи, выражающиеся неравенствами, не рассматриваются. Таким образом, 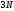координат связаны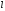уравнениями и независимых координат будет.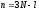

Любые декартовых координат можно задать независимо друг от друга. Остальные координаты определятся из уравнений связей. Вместонезависимых декартовых координат можно выбрать любые другие независимые параметры, зависящие от всех или части декартовых координат точек системы. Этинезависимые параметры, определяющие положение системы в пространстве, называются обобщенными координатами системы. В общем случае они могут зависеть от всех декартовых координат точек системы, т. е.

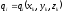, (ПИ.5)

где 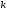изменяется от 1 до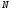. Задание обобщенных координат полностью определяет положение точек системы относительно выбранной системы отсчета, например декартовых осей координат.

Соответственно, для радиуса-вектора каждой точки системы 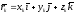, получим

. (ПИ.6)

В случае стационарных связей время явно не входит в уравнения связей. Для голономных систем вектор возможного перемещения точки в соответствии с (ПИ.6) можно выразить в форме

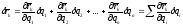. (ПИ.7)

Система, имеющая независимых обобщенных координат, характеризуется такженезависимыми возможными перемещениями или вариациями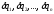, если связи голономны.Для голономных систем число независимых возможных перемещений совпадает с числом независимых обобщенных координат. Следовательно, число степеней свободы голономной системы равно числу независимых обобщенных координат этой системы, т. е..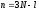

Обобщенные силы

Запишем сумму элементарных работ сил, действующих на точки системы, на возможном перемещении системы:

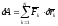. (ПИ.8)

Подставляя (ПИ.7) в (ПИ.8) и изменяя порядок суммирования по индексам 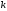и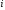, получим

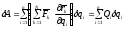. (ПИ.8')

где скалярная величина

называется обобщенной силой, отнесенной к обобщенной координате. Используя известное выражение для скалярного произведения двух векторов, сообщенную силу можно также представить в виде

, (ПИ.9)

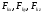–проекции силы на оси координат; 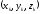– координаты точки приложения силы.

Размерность обобщенной силы в соответствии с (ПИ.8') следующим образом зависит от размерности 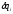, совпадающей с размерностью: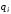

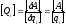, (ПИ.10)

т. е. размерность обобщенной силы равна размерности работы силы (энергии) или момента силы, деленной на размерность обобщенной координаты, к которой отнесена обобщенная сила. Из этого следует, что обобщенная сила может иметь размерность силы или момента силы.

Вычисление обобщенной силы

Обобщенную силу можно вычислить по формуле (ПИ.9), ее определяющей, т.е.

.

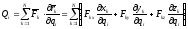Обобщенные силы можно вычислять как коэффициенты при соответствующих вариациях обобщенных координат в выражении для элементарной работы (ПИ.8'), т. е.

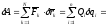
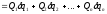. (ПИ.8'')

Наиболее целесообразен способ вычисления обобщенных сил, который получается из (ПИ.8''), если системе сообщить такое возможное перемещение, при котором изменяется только одна обобщенная координата, а другие при этом не изменяются. Так, если , а остальные, то из (ПИ.8') имеем

.

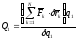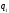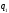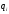Индекс указывает, что сумма элементарных работ вычисляется на возможном перемещении, при котором изменяется (варьируется) только координата. Если варьируемой координатой является, то

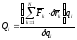. (ПИ.11)