Теорема о проекциях скоростей

При любом движении твердого тела проекции скоростей точек на прямую, соединяющую эти точки, равны(рис. Е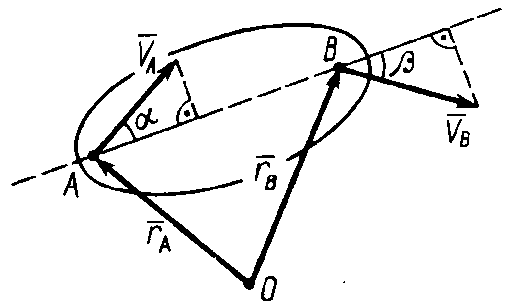.7):

. (ПЕ.17)

Рис. ПЕ.6

Приложение ж

(рекомендуемое)

Динамика Работа силы

Работа силы на каком-либо перемещении является одной из основных характеристик, оценивающих действие силы на этом перемещении.

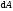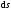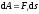Элементарная работа силына элементарном (бесконечно малом) перемещенииопределяется следующим образом (рис. ПЖ .1):

, (ПЖ .1)

где 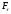– проекция силы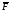на направление скорости точки приложения силы или на направление элементарного перемещения, которое считается направленным по скорости точки.

Рис. ПЖ .1

Элементарную работу можно представить, в виде:

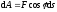, (ПЖ .2)

элементарная работа силы равна произведению элементарного перемещения ни проекцию силы на это перемещение. Отметим частые случаи, которые можно получить из (ПЖ .2):

, ;

, ;

, .

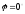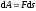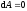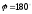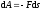Таким образом, если сила перпендикулярна элементарному перемещению, то ее элементарная работа равна нулю. В частности, работа нормальной составляющей к скорости силы всегда равна нулю.

Приведем другие формулы для вычисления элементарной работы силы:

, (ПЖ .3)

элементарная работа силы равна скалярному произведению силы на дифференциал радиуса-вектора точки приложения силы.

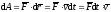, (ПЖ .4)

элементарная работа равна скалярному произведению элементарного импульса силы на скорость точки.

Аналитическое выражение элементарной работы:

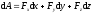. (ПЖ .5)

Полная работа силы 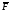на перемещении от точки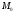до точки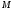равна:

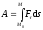, (ПЖ .6)

Используя другие выражения для элементарной работы, полную работу силы можно представить также в виде

, (ПЖ .8)

или

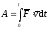, (ПЖ .9)

где момент времени 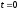соответствует точке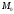, а момент времени– точке.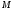

Из определения элементарной и полной работы следует:

1. работа равнодействующей силы на каком-либо перемещении равна алгебраической сумме работ составляющих сил на том же перемещении;

2. работа силы на полном перемещении равна сумме работ этой же силы на составляющих перемещениях, на которые любым образом разбито все перемещение.

Примеры вычисления работы силы

Работа силы в общем случае зависит от характера движения точки приложения силы. Следовательно, для вычисления работы надо знать движение этой точки. Но в природе имеются силы и примеры движения, для которых работу можно вычислить сравнительно просто, зная начальное и конечное положение точки.

Работа силы тяжести. Силу тяжести материальной точки массойвблизи поверхности Земли можно считать постоянной, равной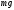, направленной по вертикали вниз. Если взять оси координат, где ось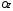направлена по вертикали вверх, то

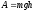, (ПЖ .10)

где 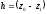– высота опускания точки.

При подъеме точки высота 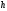является отрицательной. Следовательно, в общем случае работа силы тяжести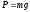равна

. (ПЖ .11)

Если имеем систему материальных точек, то для каждой точки с массой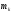будем иметь работу ее силы тяжести

,

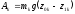где 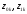– начальная и конечная координаты точки.

Работа всех сил тяжести системы материальных точек

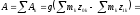
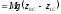, (ПЖ .12)

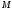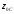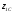где – масса системы точек;и– начальная и конечная координаты центра масс системы точек. Вводя обозначение для изменения высоты центра масс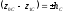, имеем

. (ПЖ .12')

Работа линейной силы упругости. Линейной силой упругости (или линейной восстанавливающей силой) называют силу, действующую по закону Гука:

,

где – расстояние от точки равновесия, где сила равна нулю, до рассматриваемой точки;– постоянный коэффициент жесткости.

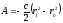. (ПЖ .13)

По этой формуле вычисляют работу линейной силы упругости пружины при перемещении по любому пути из точки 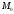, в которой ее удлинение (начальная деформация) равно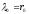, в точку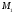, где деформация соответственно равна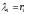. В новых обозначениях (ПЖ .13) принимает вид

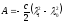. (ПЖ .13')

Работа силы, приложенной к твердому телу:

1. При поступательном движении твердого тела все точки тела имеют одинаковые по модулю и направлению скорости. Следовательно, если сила 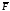приложена к точке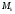, то, так как,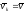

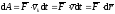, (ПЖ .14)

где – радиус-вектор произвольной точки твердого тела. На каком-либо перемещении полная работа

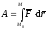. (ПЖ .15)

2. При вращении твердого тела вокруг неподвижной оси скорость точки можно вычислить по векторной формуле Эйлера:

,

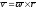тогда элементарную работу силы 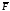определим по формуле

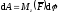. (ПЖ .16)

Таким образом, элементарная работа силы, приложенной к какой-либо точке тела, вращающегося вокруг неподвижной оси, равна произведению момента силы относительно оси вращения на дифференциал угла поворота тела.

Полная работа

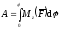. (ПЖ .17)

В частном случае, если момент силы относительно оси вращения является постоянным, т. е. 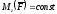, работу определяют по формуле

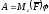. (ПЖ .18)

3. Для свободного тела в общем случае движения скорость точки 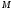, в которой приложена сила,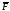

,

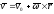следовательно,

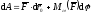. (ПЖ .19)

Таким образом, элементарная работа силы, приложенной в какой-либо точке твердого тела, в общем случае движения складывается из элементарной работы на элементарном поступательном перемещении вместе с какой-либо точкой тела и на элементарном вращательном перемещении вокруг этой точки.

В случае вращения твердого тела вокруг неподвижной точки, выбрав эту точку за полюс , для элементарной работы имеем

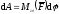. (ПЖ .20)

Поворот на угол 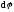следует рассматривать в каждый момент времени вокруг своей мгновенной оси вращения.

Работа внутренних сил твердого тела. Для твердого тела сумма работ внутренних сил равна нулю при любом его перемещении.