Плоское (плоскопараллельное) движение твердого тела

Плоским движением твердого тела называют такое его движение, при котором каждая его точка все время движется в одной и той же плоскости. Плоскости, в которых движутся отдельные точки, параллельны между собой и параллельны одной и той же неподвижной плоскости. Поэтому плоское движение твердого тела часто называют плоскопараллельным движением. Траектории точек тела при плоском движении являются плоскими кривыми.

Пусть твердое тело совершает плоское движение, параллельное неподвижной плоскости (рис. ПЕ.4). Тогда любая прямая, перпендикулярная этой плоскости и жестко скрепленная своими точками с движущимся телом, будет двигаться поступательно, т. е. все точки этой прямой движутся одинаково.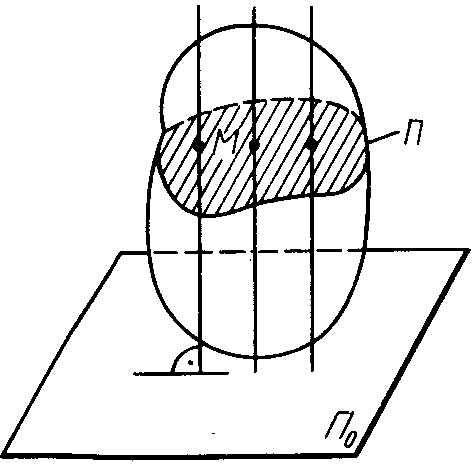

Рис. ПЕ.4

Для изучения плоского движения твердого тела достаточно изучить движение точек этого тела, лежащих в какой-либо плоскос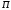ти , параллельной неподвижной плоскости , т.е. точек тела, лежащих в сечении рассматриваемого тела плоскостью и образующих плоскую фигуру.

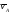Плоское движение точки тела можно разложить на две составляющие: поступательное движение вместе с какой-либо точкой тела (полюсом) со скоростьюи ускорением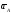и вращательное точки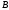вокруг полюса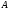со скоростью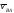и ускорением.

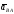Тогда по теореме сложения скоростей скорость какой-либо точки плоской фигуры при плоском движении равна векторной сумме скоростей полюса и скорости этой точки от вращательного движения плоской фигуры вокруг полюса

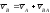, (ПЕ.6)

где

, (ПЕ.7)

а вектор 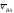перпендикулярен отрезку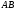и направлен в сторону вращения плоской фигуры.

По теореме сложения ускорений:

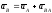, (ПЕ.8)

т. е. ускорение какой-либо точки плоской фигуры при плоском движении равно векторной сумме ускорения полюса и ускорения этой точки от вращательного движения плоской фигуры вокруг полюса.

Ускорение от относительного вращательного движения вокруг полюса, как и в случае вращения тела вокруг неподвижной оси, состоит из касательной и нормальной составляющих 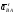и:

, (ПЕ.9)

причем

, (ПЕ.10)

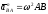, (ПЕ.11)

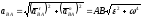. (ПЕ.12)

Касательное относительное ускорение 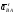направлено по перпендикуляру к отрезкув сторону дуговой стрелки углового ускорения. Нормальное относительное ускорение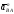соответственно направлено по линииот точки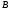к полюсу.

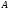В каждый момент времени при плоском движении фигуры в ее плоскости, если 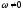, имеется единственная точка этой фигуры, скорость которой равна нулю. Эту точку называют мгновенным центром скоростей (МЦС). Обозначим ее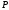(рис. ПЕ.5).

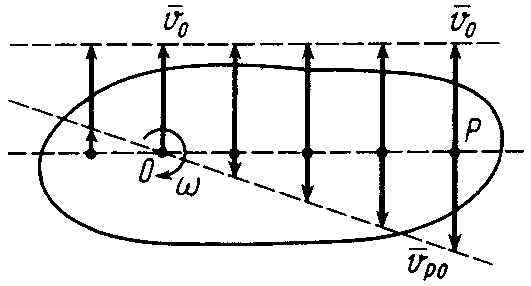
Рис. ПЕ.5

Мгновенный центр скоростей находится на перпендикуляре к скорости , проведенном из точки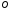, на расстоянии.

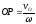Мгновенный центр скоростей является единственной точкой плоской фигуры для данного момента времени. В другой момент времени мгновенным центром является уже другая точка плоской фигуры.

Если мгновенный центр известен, то, приняв его за полюс и учитывая, что скорость его в этом случае равна нулю, согласно (ПЕ.6) и (ПЕ.7), для точки 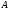фигуры имеем

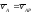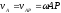, , (ПЕ.13)

где 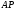– расстояние от точки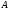до мгновенного центра скоростей.

По направлению скорость 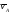в этом случае перпендикулярна отрезку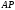. Для точки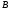, аналогично,

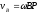, (ПЕ.14)

причем скорость 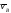перпендикулярна отрезку. Получаем:

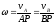, (ПЕ.15)

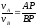, (ПЕ.16)

Следовательно, если мгновенный центр скоростей известен, то скорости точек плоской фигуры при ее движении в своей плоскости вычисляют так же, как и в случае вращения фигуры в рассматриваемый момент вокруг своего мгновенного центра скоростей с угловой скоростью .

Для нахождения скоростей точек тела при его плоском движении обычно предварительно находят мгновенный центр скоростей. Но можно применить формулу, выражающую зависимость между скоростями двух точек тела.