
Контрольная работа №2
7. Классическим методом найти частное
решение системы дифференциальных
уравнений удовлетворяющее начальным условиям
удовлетворяющее начальным условиям![]() .
.
Решение.Решением этой системы
является пара функций![]() ,
,![]() ,
удовлетворяющих системе, причем
,
удовлетворяющих системе, причем
![]() .
.
Продифференцируем первое уравнение по
переменной
![]() :
:
![]() .
.
Из первого уравнения определяем
![]() ,
следовательно, из второго уравнения
имеем
,
следовательно, из второго уравнения
имеем
![]() .
.
Подставляем
![]() в уравнение, полученное после
дифференцирования, приходим к уравнению
в уравнение, полученное после
дифференцирования, приходим к уравнению
![]() ,
,
![]() – линейное дифференциальное уравнениеIIпорядка с
– линейное дифференциальное уравнениеIIпорядка с
постоянными коэффициентами.
Составляем характеристическое уравнение и находим его корни:
![]()
![]() – действительные различные корни.
– действительные различные корни.
В этом случае общее решение дифференциального уравнения имеет вид
![]() ,
,
![]() .
.
Ранее определили
![]() .
Тогда
.
Тогда
![]() .
.
Общее решение системы
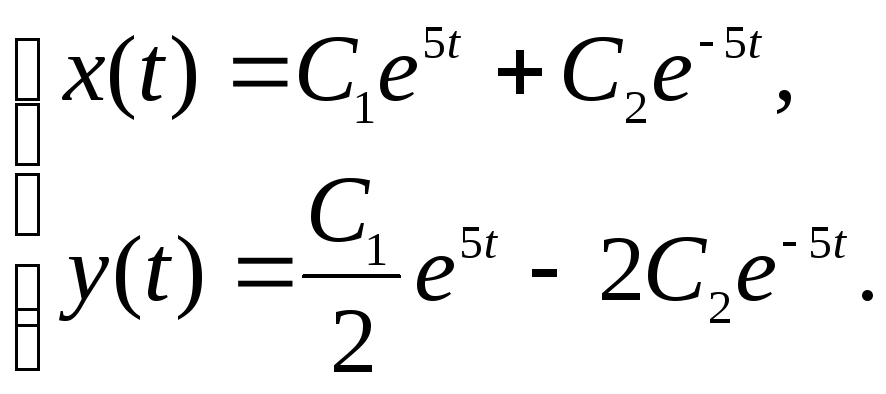
Находим значения произвольных постоянных,
используя начальные условия
![]() :
:
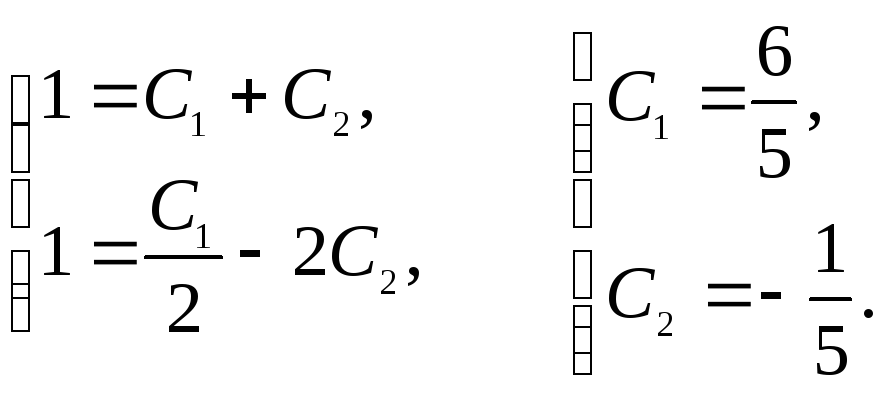
Частное решение системы
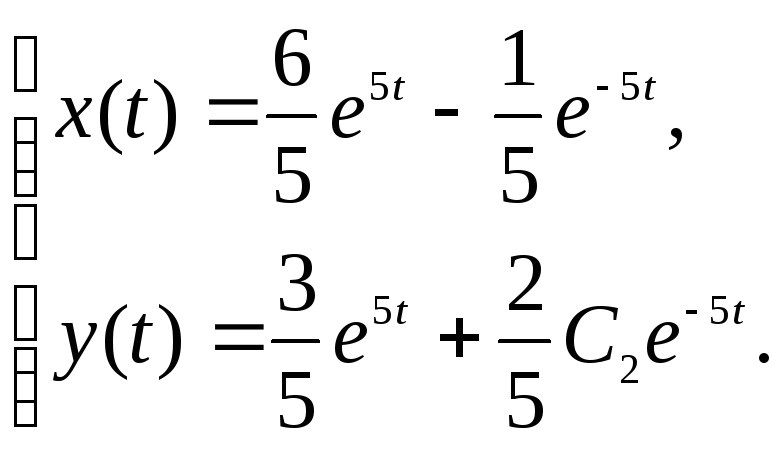
8.Вычислить определённый интервал с точностью до 0,001 путём разложения подынтегральной функции в ряд и почленного интегрирования этого ряда.
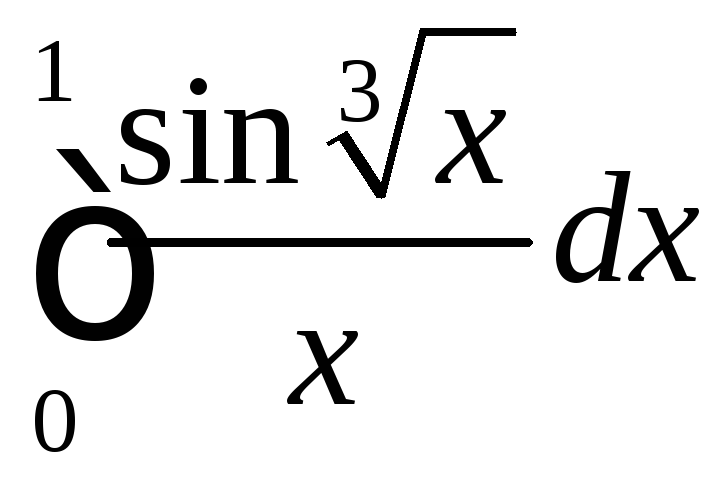
Решение.
Разложим подынтегральную функцию в степенной ряд по формуле
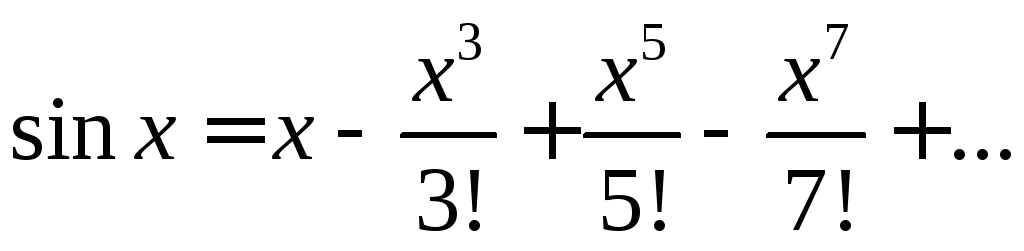 Тогда
Тогда
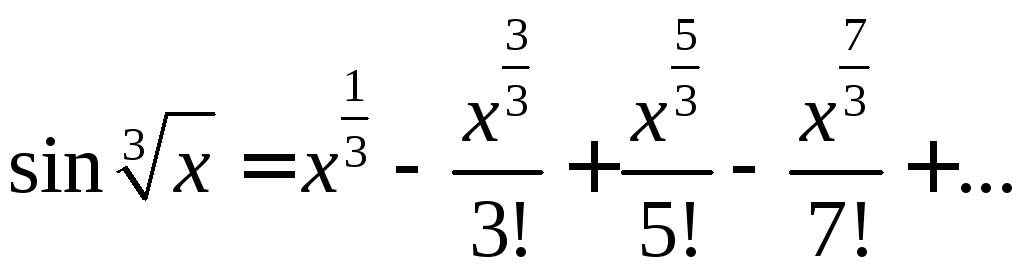
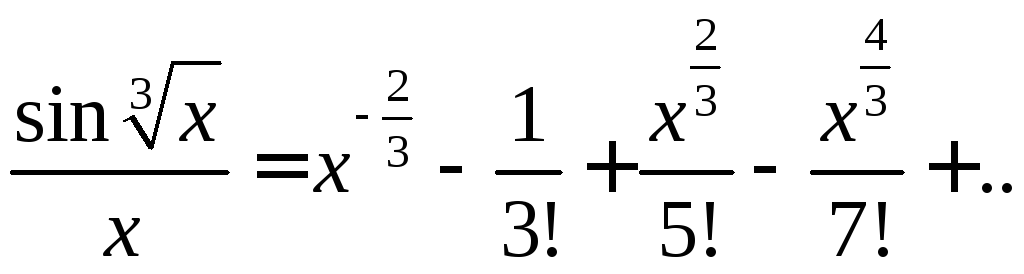


![]()
Полученный знакочередующийся ряд удовлетворяет условиям теоремы Лейбница. Так как четвёртый его член по абсолютной величине меньше 0,001, то для обеспечения заданной точности достаточно взять первые три члена ряда. Получаем:
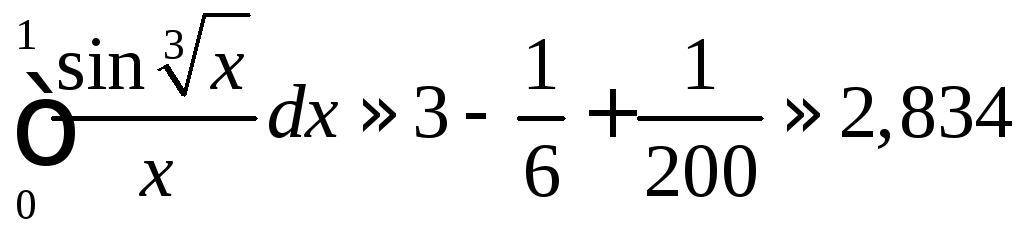 .
.
.
9.Разложить заданную функцию![]() в ряд Фурье по синусам на отрезке
в ряд Фурье по синусам на отрезке![]() .
.
Решение. Так как по условию ряд
должен содержать только синусы кратных
углов, то следует продолжить заданную
функцию на отрезок![]() нечетным образом, затем продолжить на
всю числовую ось с периодом
нечетным образом, затем продолжить на
всю числовую ось с периодом![]() .
Теперь разложим полученную периодическую
функцию в ряд Фурье (эта операция
разложения называется гармоническим
анализом) вида:
.
Теперь разложим полученную периодическую
функцию в ряд Фурье (эта операция
разложения называется гармоническим
анализом) вида:
![]() .
.
Так как заданная функция нечетная, то
коэффициенты ряда Фурье
![]() ,
а
,
а![]() вычисляем по формуле
вычисляем по формуле
![]()
и ряд Фурье имеет вид
![]() .
.
Подставляя заданную функцию, получаем
![]() .
.
Последний интеграл вычисляем методом
интегрирования по частям, полагая
![]() .
Отсюда
.
Отсюда![]() .
следовательно,
.
следовательно,
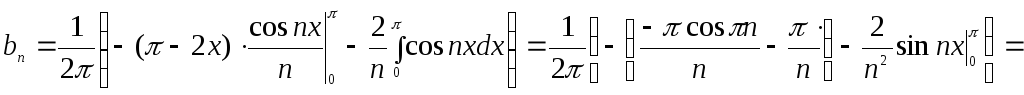
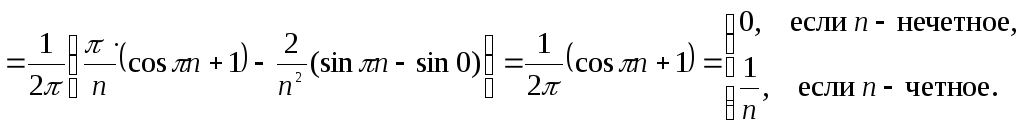
Таким образом, искомое разложение имеет вид
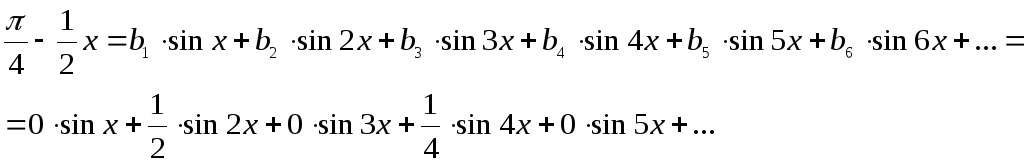
или
![]()
10.Дана функция
двух переменных![]() .
Найти:
.
Найти:
1) экстремум функции
![]() ;
;
2)
![]() в точкеА(1; –2);
в точкеА(1; –2);
3) наибольшую скорость возрастания
![]() точкеА(1; –2).
точкеА(1; –2).
Решение.1) Для отыскания экстремума
функции![]() предварительно
найдем частные производные первого и
второго порядка:
предварительно
найдем частные производные первого и
второго порядка:
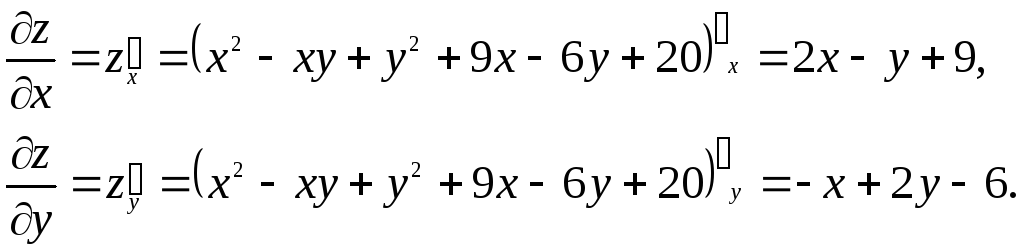
Приравняем их к нулю и решим систему уравнений:
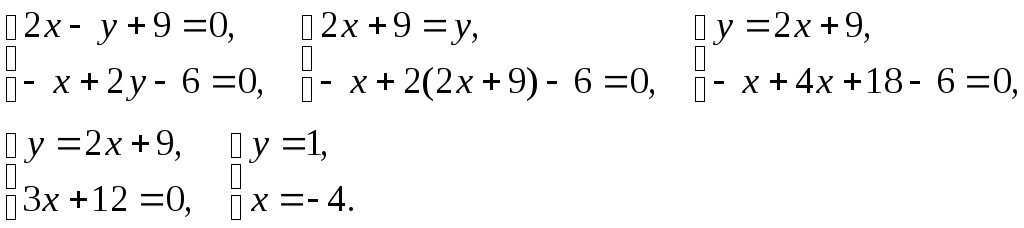
Решением системы является точка М(–4; 1). ТочкаМ(–4; 1) называется подозрительной на экстремум. Найдем частные производные второго порядка в точкеМ:
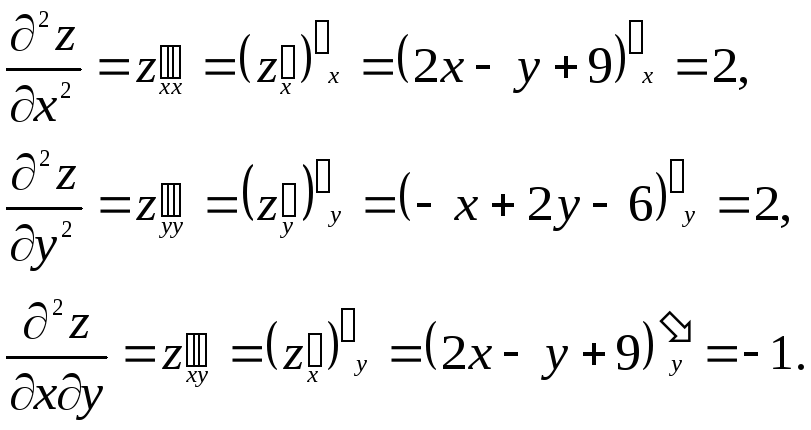
Из них составим определитель второго порядка
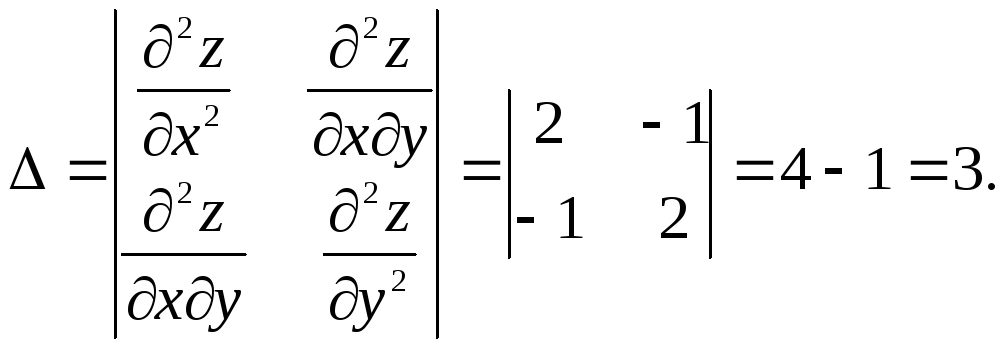
Так как
![]() ,
то в точкеМ(–4; 1) есть экстремум.
Производная
,
то в точкеМ(–4; 1) есть экстремум.
Производная![]() ,
а, значит, это точка минимума функции.
,
а, значит, это точка минимума функции.
2) Градиент функции
![]() найдем по формуле:
найдем по формуле:
![]() ,
,![]() и
и![]() были найдены в пункте 1.
были найдены в пункте 1.
![]() .
.
Градиент функции
![]() в точкеА(1; –2):
в точкеА(1; –2):
![]() .
.
3) Наибольшая скорость возрастания функции равна модулю градиента:
![]() .
.
11.Вычислить массу неоднородной
пластинки треугольной формы с вершинами
в точках О (0;0) , А (5;0) , В (0;7) , поверхностная
плотность которой в точке М (х;у) равна![]() .
.
Решение.
Изобразим пластинку на плоскости xOy.
 у
у
 В
В
