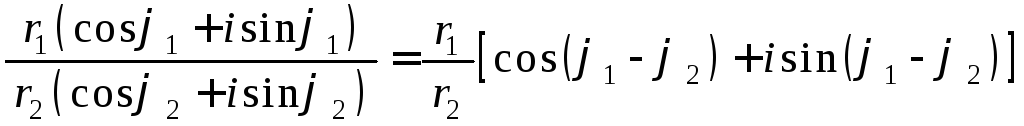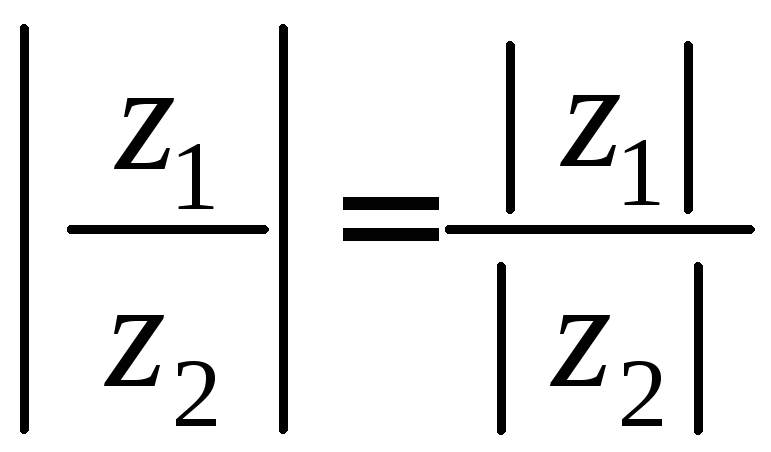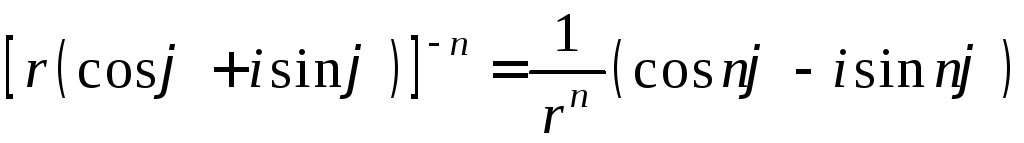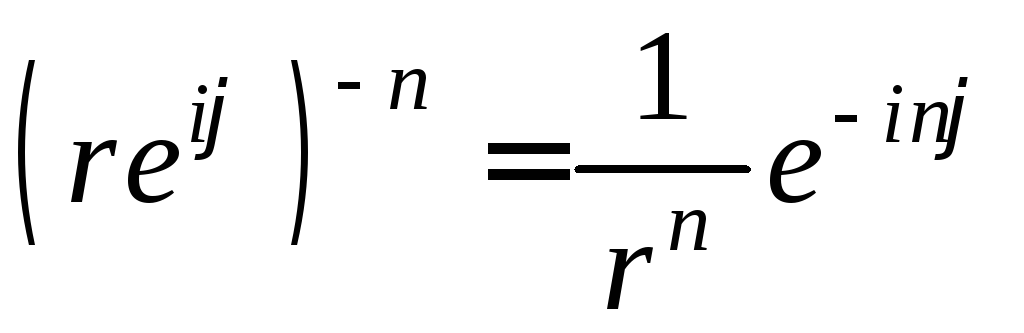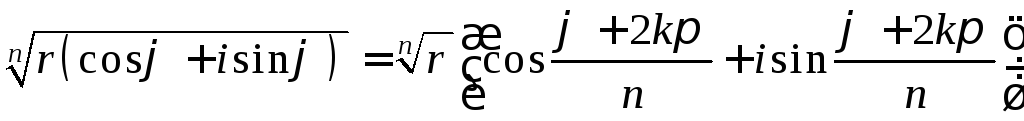3. Умножение и деленин комплексных чисел в тригонометрической и покзательной форме

Тригонометрическая и показательная формы комплексного числа позволяют относительно просто выполнить операции умножения и деления комплексных чисел. Действительно, пусть даны комплексные числа в тригонометрической форме

. (3.1)

Найдем их произведение и частное:

,

.

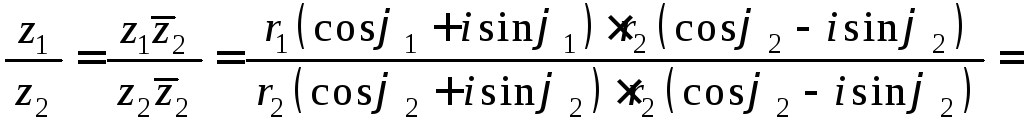
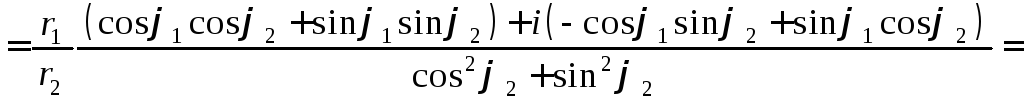
Таким образом, нами получены правила:

– при умножении двух комплексных чисел, заданных в тригонометрической форме получается комплексное число, модуль которого равен произведению модулей этих чисел, а аргумент – сумме их аргументов;

– при делении одного комплексного числа на другое, заданных в тригонометрической форме получается комплексное число, модуль которого равен отношению модулей первого и второго числа, а аргумент – разности их аргументов.

На языке модуля и аргумента комплексного числа полученные свойства можно представить в виде:

Пусть комплексные числа заданы в показательной форме

.

Найдем их произведение и частное:

,

.

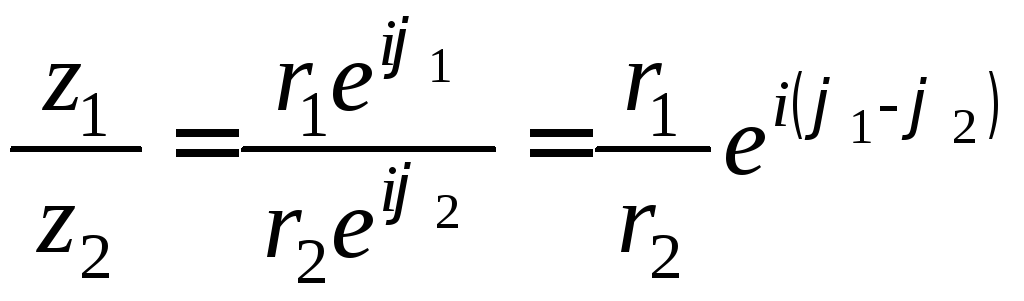Полученные равенства показывают, что и в этом случае имеют места свойства для модуля и аргумента произведения и частного.

4. Возведение в степень и извлечение корня из комплексного числа

Полученные свойства умножения и деления комплексных чисел в тригонометрической и показательной форме позволяют эффективно выполнить операции возведения комплексного числа, в любую целую степень, и извлекать корень любой степени.

Пусть – произвольное целое число. В этом случае справедливо равенство

.

Это равенство называется формулой Муавра. Справедливость этой формулы выводится из формулы умножения комплексных чисел в тригонометрической форме, полученной в § 3.

Формулу Муавра в показательной форме можно записать так:

.

Таким образом, при возведении комплексного числа в целую положительную степень, его модуль возводится в эту степень, а аргумент умножается на эту степень.

Рассмотрим, теперь отрицательную степень. В этом случае, будем иметь

,

.

Рассмотренные до сих пор все арифметические и алгебраические операции над комплексными числами определялись однозначно, то есть в результате получалось единственное число. Операция извлечения корня из комплексного числа определяется неоднозначно, то есть в результате даетразличных комплексных чисел.

Комплексное число называетсякорнем -й степени из комплексного числа , если-я степень числаравна, то есть. Пусть. Тогда каждое из чисел

,

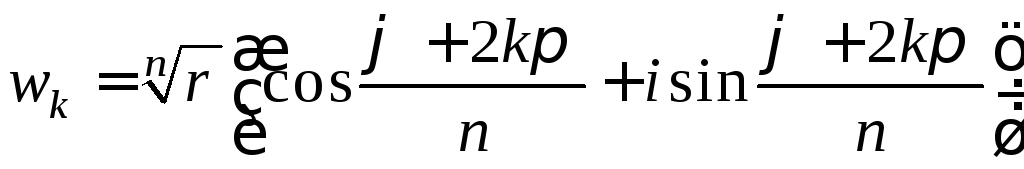является корнем -й степени из комплексного числа. Действительно, так как

,

для любого , то имеем

.

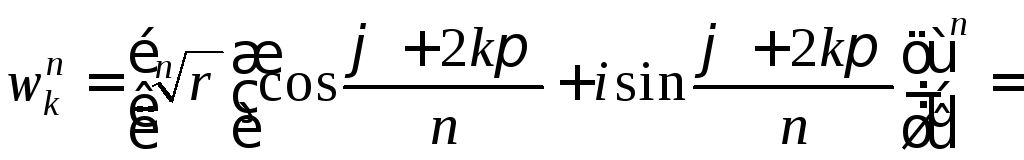
Полученные формулы для возведения в целую степень, и извлечения корня из комплексного числа позволяют вычислить любую дробную степень из произвольного комплексного числа. Это следует из любого из представлений

или ,

то есть либо вначале нужно извлекать корень -й степени, а затем полученные числа возвести в-ю степень, либо вначале данное число возвести в-ю степень, а затем извлекать корень-й степени. В обоих случаях, при, получатсяразличных значений. Только приполучится одно значение, независимо от значения.