I. Теоретический раздел

1. Основные определения

Комплексным числом называется выражение вида

, (1.1)

где и– вещественные числа, а–мнимая единица: . Часто бывает удобным обозначать комплексное число (1.1) одной буквой:

. (1.2)

Число называетсявещественной частью комплексного числа и обозначается(от французского словаreelle – «вещественный»):

, (1.3)

а число –мнимой частью комплексного числа и обозначается(от французского словаimaginaire – «мнимый»):

. (1.4)

Рассмотрим частные случаи. Если , то вместо записибудет использовано обозначениеи комплексное число являетсячисто вещественным. Таким образом, множество вещественных чисел является подмножеством множества комплексных чисел:

. (1.5)

Если , то вместо записибудет использовано обозначениеи комплексное число называетсячисто мнимым.

Если же , то вместо записибудет использовано обозначениеи комплексное число называетсянулем, которое совпадает с вещественным нулем.

Комплексные числа, у которых совпадают вещественные части, а мнимые части отличаются только знаками, называются комплексно сопряженными. Таким образом, числа иявляются комплексно сопряженными. В дальнейшем вместо записибудет использовано более короткое обозначение:. Если комплексное число обозначено, то его комплексно сопряженное обозначается. Заметим, что комплексно сопряженное к комплексному числу, то есть, совпадает с самым комплексным числом:

. (1.6)

Комплексные числа иназываютсяравными, если равны их одноименные части и обозначается :

. (1.7)

Определим арифметические операции на множестве комплексных чисел .

1. Сумма комплексных чисел иобозначаетсяи определяется равенством

. (1.8)

2. Разность комплексных чисел иобозначаетсяи определяется равенством

. (1.9)

3. Произведение комплексных чисел иобозначаетсяилии определяется равенством

. (1.10)

4. Деление комплексного числа на комплексное числообозначаетсяилии определяется равенством

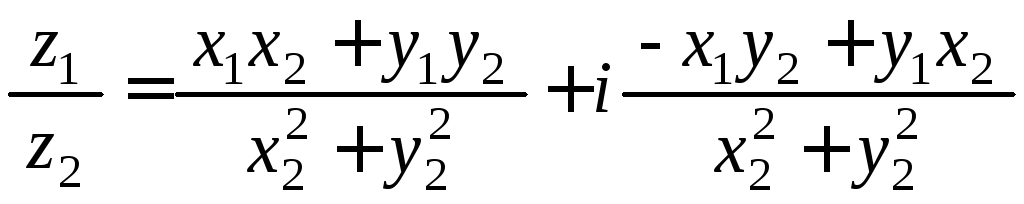. (1.11)

Замечание. Арифметические операции (1.8) – (1.11) над комплексными числами получаются, естественным образом, по правилам сложения и умножения многочленов и, имея в виду равенство. Действительно, имеем

,

,

,

.

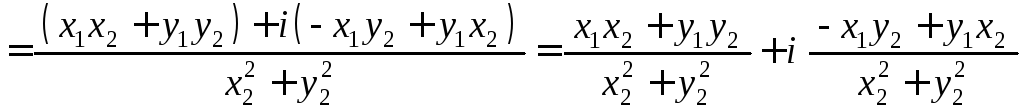Таким образом, при делении одного комплексного числа на другое числитель и знаменатель дроби нужно умножить на сопряженное знаменателя:

.

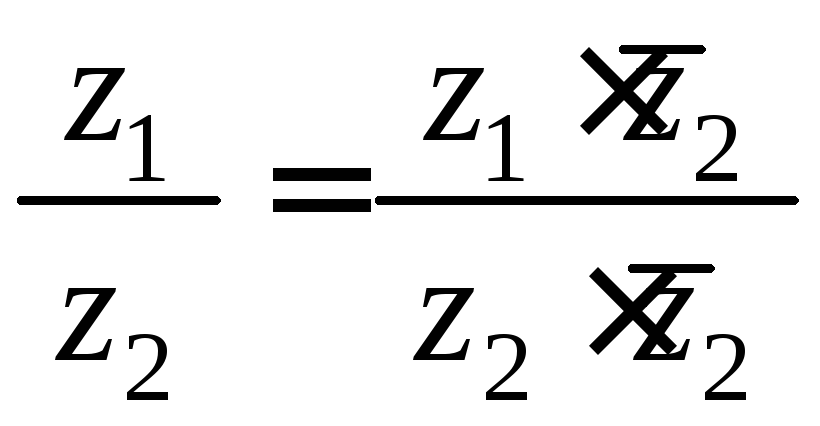Для произвольных комплексных чисел выполнены следующие законы:

1) коммутативность сложения: ,

2) коммутативность умножения: ,

3) ассоциативность сложения: ,

4) ассоциативность умножения: ,

5) дистрибутивность относительно сложения и умножения:

.

Покажем, что сумма и произведение любого комплексного числа с его комплексно сопряженным являются вещественными числами. Пусть . Тогда

, (1.12)

. (1.13)

Действительно, имеем

,

.

Пример 1. Даны комплексные числа . Найти: а); б); в); г); д); е); ж); з).

Решение. Согласно определению операций над комплексными числами, имеем:

а) ;

б) ;

в) ;

г) ;

д) ;

е) ;

ж)

;

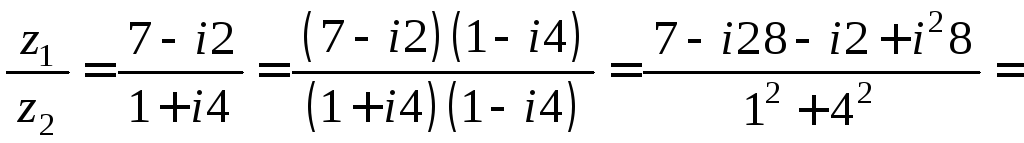
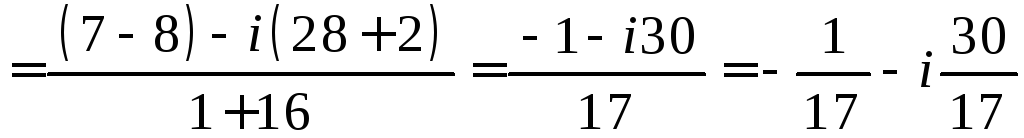з)

.
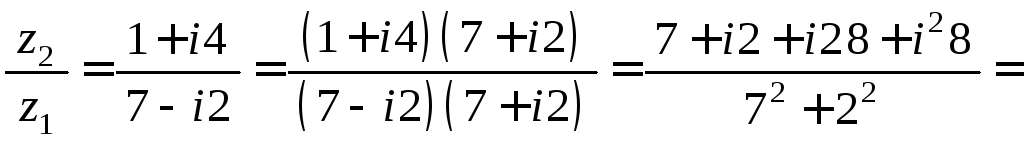
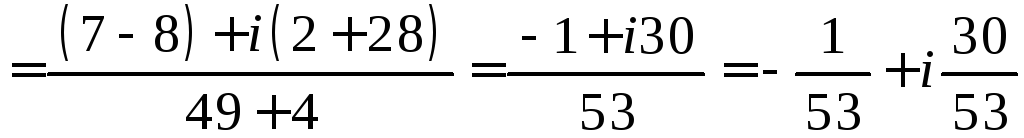