
- •0. Введение
- •I. Теоретический раздел
- •1. Основные определения
- •2. Геометрическое изображение комплексного числа. Понятие о модуле и аргументе
- •3. Умножение и деленин комплексных чисел в тригонометрической и покзательной форме
- •4. Возведение в степень и извлечение корня из комплексного числа
- •II. Справочный раздел
- •1. Табличные значения аргументов некоторых комплексных чисел
- •3. Формулы для степеней и корней
- •III. Практический раздел Образцы решения задач и их оформления
II. Справочный раздел
1. Табличные значения аргументов некоторых комплексных чисел
|
№ |
Комплексные числа |
Стандартные значения
|
Главные значения
| ||
|
в градусах |
в радианах |
в градусах |
в радианах | ||
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
7 |
|
|
|
|
|
|
8 |
|
|
|
|
|
|
9 |
|
|
|
|
|
|
10 |
|
|
|
|
|
|
11 |
|
|
|
|
|
|
12 |
|
|
|
|
|
|
13 |
|
|
|
|
|
|
14 |
|
|
|
|
|
|
15 |
|
|
|
|
|
|
16 |
|
|
|
|
|
2. Формулы сокращенного умножения
2.1. Квадрат суммы: ![]() ;
;
2.2. Квадрат
разности: ![]() ;
;
2.3. Разность
квадратов: ![]() ;
;
2.4. Куб суммы: ![]() ;
;
2.5. Куб разности: ![]() ;
;
2.6. Разность
кубов: ![]() ;
;
2.7. Сумма кубов: ![]() .
.
3. Формулы для степеней и корней
6.1. Произведение
степеней с одинаковыми основаниями:
![]() ;
;
6.2. Произведение
степеней с одинаковыми показателями:
![]() ;
;
6.3. Отношение
степеней с одинаковыми основаниями:
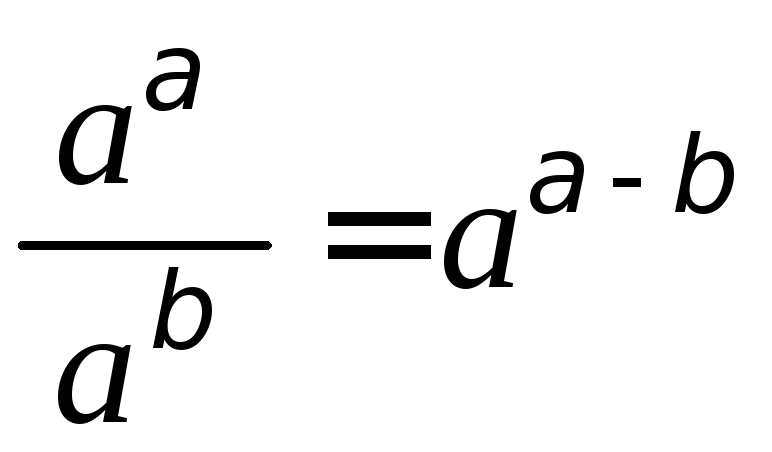 ;
;
6.4. Отношение
степеней с одинаковыми показателями:
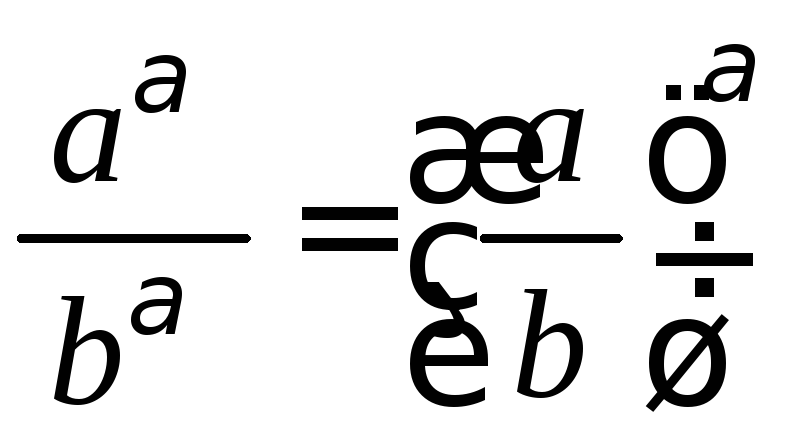 ;
;
6.5. Возведение
степени в степень:
![]() ;
;
6.6. Степень с
отрицательным показателем:
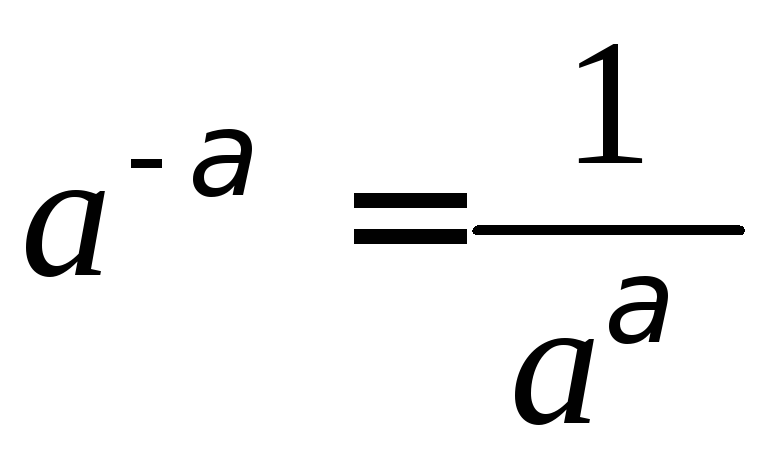 ;
;
6.7. Произведение
корней:
![]() ;
;
6.8. Отношение
корней:
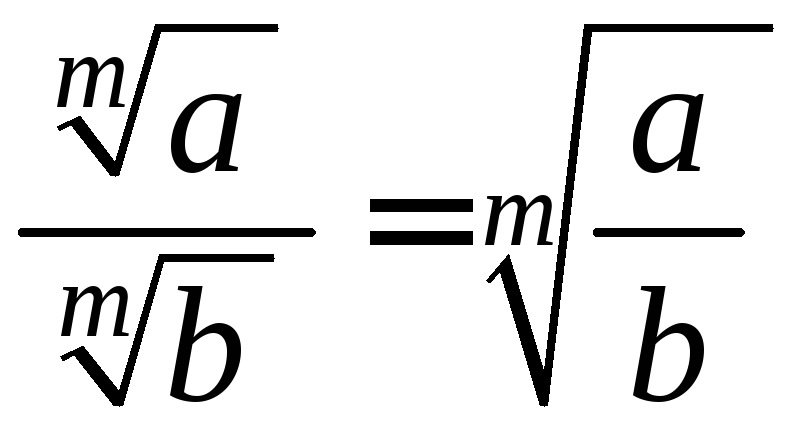 ;
;
6.9. Замена корня
дробной степенью:
![]() .
.
III. Практический раздел Образцы решения задач и их оформления
Задача 1.а.
Найти сумму комплексных чисел
![]() и
и![]() .
Ответ записать в
алгебраической и
тригонометрической форме.
.
Ответ записать в
алгебраической и
тригонометрической форме.
![]()
![]() ,
,
![]()
![]() .
.
Решение. По определению суммы комплексных чисел имеем:
![]() ,
,
![]() .
.
Найдем модуль и
аргумент комплексного числа
![]() :
:
![]() ;
;
![]() ,
,
 ;
;
![]() .
.
Ответ: ![]() – алгебраическая форма,
– алгебраическая форма,
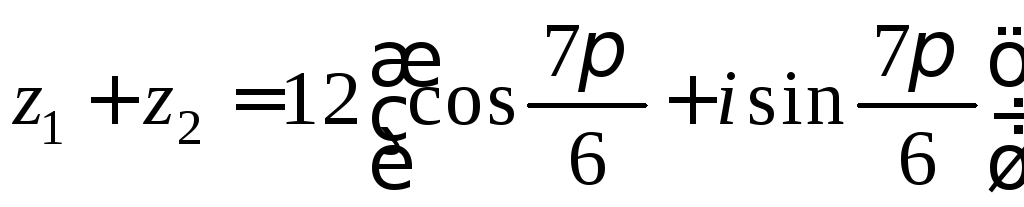 –тригонометрическая
форма.
–тригонометрическая
форма.
Задача 1.б.
Найти сумму комплексных чисел
![]() и
и![]() .
Ответ записать в
алгебраической и
показательной форме.
.
Ответ записать в
алгебраической и
показательной форме.
![]() ,
,
![]() .
.
Решение. По определению суммы комплексных чисел имеем:
![]() ,
,
![]() .
.
Найдем модуль и
аргумент комплексного числа
![]() :
:
![]() ;
;
![]() ,
,
 ;
;
![]() .
.
Ответ: ![]() – алгебраическая форма,
– алгебраическая форма,
![]() –показательная
форма.
–показательная
форма.
Задача 2.а.
Найти разность комплексных чисел
![]() и
и![]() .
Ответ записать в алгебраической и
показательной форме.
.
Ответ записать в алгебраической и
показательной форме.
![]()
![]() ,
,
![]()
![]() .
.
Решение. По определению разности комплексных чисел имеем:
![]()
![]() ,
,
![]() .
.
Найдем модуль и
аргумент комплексного числа
![]() :
:
![]() ;
;
![]() ,
,
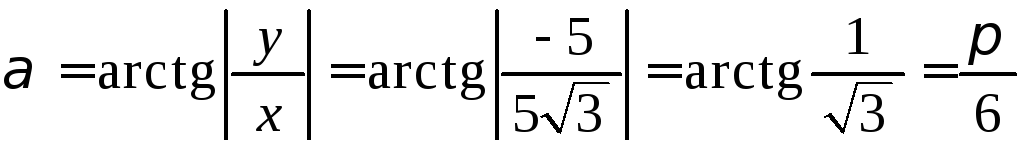 ;
;
![]() .
.
Ответ: ![]() – алгебраическая форма,
– алгебраическая форма,
![]() – показательная форма.
– показательная форма.
Задача 2.б.
Найти разность комплексных чисел
![]() и
и![]() .
Ответ записать в алгебраической и
тригонометрической форме.
.
Ответ записать в алгебраической и
тригонометрической форме.
![]() ,
,
![]() .
.
Решение. По определению разности комплексных чисел имеем:
![]()
![]() ,
,
![]() .
.
Найдем модуль и
аргумент комплексного числа
![]() :
:
![]() ;
;
![]() ,
,
 ;
;
![]() .
.
Ответ: ![]() – алгебраическая форма,
– алгебраическая форма,
 – тригонометрическая форма.
– тригонометрическая форма.
Задача 3.а.
Найти произведение комплексных чисел
![]() и
и![]() .
Ответ записать в алгебраической и
тригонометрической форме.
.
Ответ записать в алгебраической и
тригонометрической форме.
![]() =
=![]() ,
,![]() =
=![]()
Решение.
Учитывая, что
![]() имеем:
имеем:
![]()
![]() ,
,
![]() .
.
Найдем модуль и
аргумент комплексного числа
![]() :
:
![]() ;
;
![]() ,
,
![]() ,
,
 ;
;
![]() .
.
Ответ: ![]() – алгебраическая форма,
– алгебраическая форма,
 –тригонометрическая
форма.
–тригонометрическая
форма.
Задача 3.б.
Найти произведение комплексных чисел
![]() и
и![]() .
Ответ записать в алгебраической форме.
Найти приближенное значение модуля с
точностью до 0,001, а аргумента – с точностью
до целого градуса.
.
Ответ записать в алгебраической форме.
Найти приближенное значение модуля с
точностью до 0,001, а аргумента – с точностью
до целого градуса.
![]() ,
,
![]() .
.
Решение.
Учитывая, что
![]() будем иметь:
будем иметь:
![]() ,
,
![]() .
.
Найдем модуль и
аргумент комплексного числа
![]() :
:
![]() ;
;
![]()
![]() ,
,
 ;
;
![]() .
.
Ответ: ![]() – алгебраическая форма,
– алгебраическая форма,
![]() –приближенное
значение модуля,
–приближенное
значение модуля,
![]() –приближенное
значение аргумента.
–приближенное
значение аргумента.
Задача 4.а.
Найти частное
![]() .
Ответ записать в алгебраической и
показательной форме.
.
Ответ записать в алгебраической и
показательной форме.
![]() .
.
Решение. По определению частного комплексных чисел имеем:
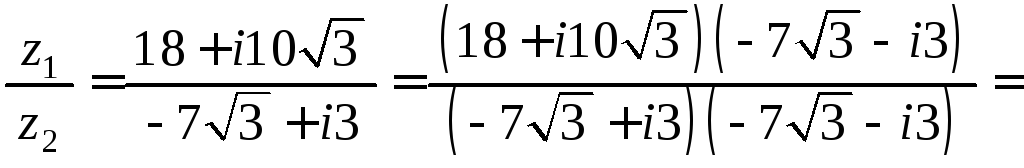
 ,
,
 .
.
Найдем модуль и
аргумент комплексного числа
![]() :
:
![]() ;
;
![]() ,
,
 ,
,
![]() .
.
Ответ:  – алгебраическая форма,
– алгебраическая форма,
 – показательная форма.
– показательная форма.
Задача 4.б.
Найти частное
![]() .
Ответ записать в алгебраической форме.
Найти приближенное значение модуля с
точностью до 0,001, а аргумента – с точностью
до целого градуса.
.
Ответ записать в алгебраической форме.
Найти приближенное значение модуля с
точностью до 0,001, а аргумента – с точностью
до целого градуса.
![]() ,
,
![]() .
.
Решение. По определению частного комплексных чисел имеем:
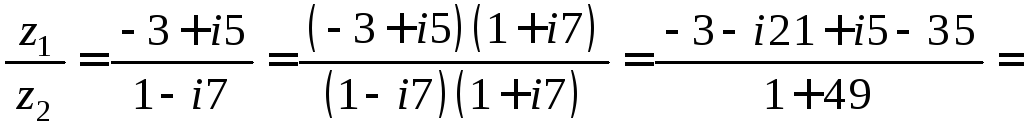
![]() ,
,
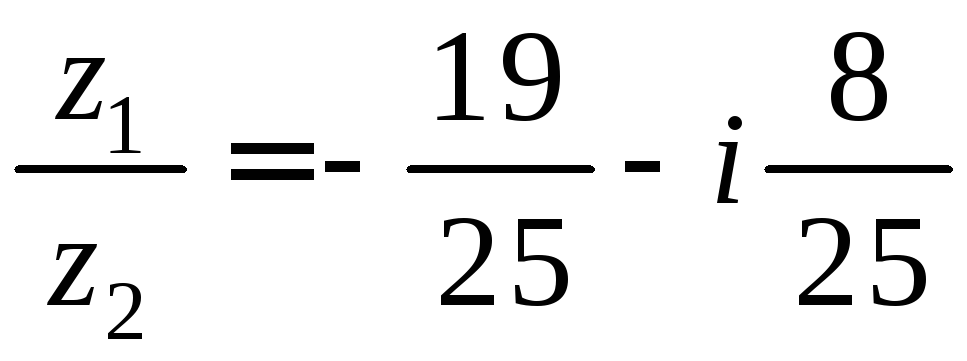 .
.
Найдем модуль и
аргумент комплексного числа
![]() :
:
![]() ;
;

 ,
,
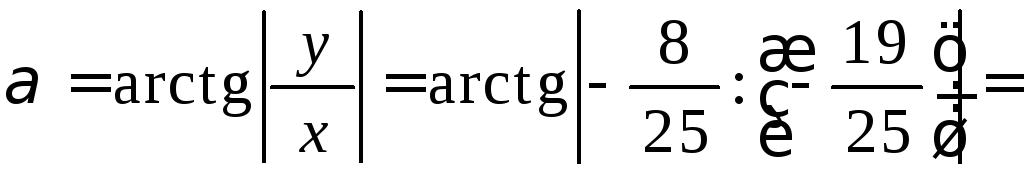
![]() ,
,
![]() .
.
Ответ: 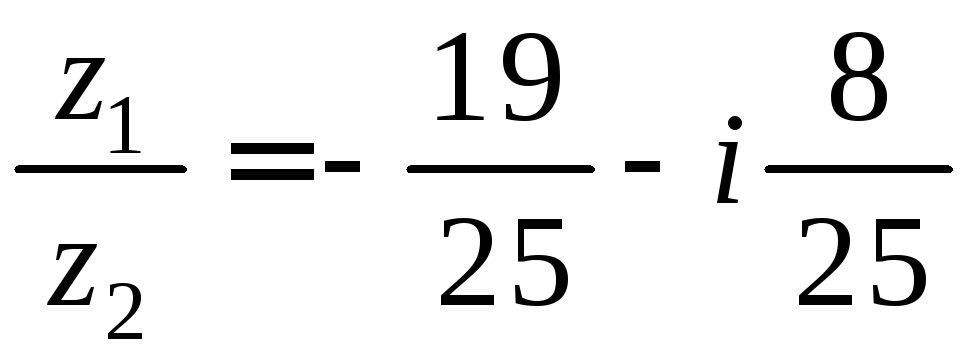 – алгебраическая форма,
– алгебраическая форма,
 –приближенное
значение модуля,
–приближенное
значение модуля,
 –приближенное
значение аргумента.
–приближенное
значение аргумента.
Задача 5.а.
Вычислить значение многочлена
![]() при
при![]() .
.
а) Ответ записать в алгебраической форме;
б) найти точное значение модуля и его приближенное значение с точностью до 0,0001;
в) найти приближенное значение аргумента в радианах с точностью до 0,001 и в градусах с точностью до целого градуса.
![]() ,
,
![]() .
.
Решение.
Вычислим
![]() :
:
![]() ,
,
![]() .
.
Вычислим значение многочлена:
![]()
![]()
![]()
![]() .
.
Найдем модуль и
аргумент комплексного числа
![]() .
.
Так как
![]() ,
то
,
то![]() .
Имеем:
.
Имеем:
![]()
![]() ;
;
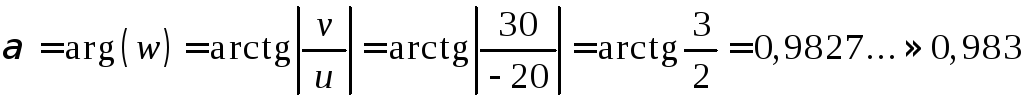 ,
,
![]() ,
,
![]() .
.
Ответ: ![]()
![]() – алгебраическая форма,
– алгебраическая форма,
![]() – точное и приближенное значения
– точное и приближенное значения
модуля ответа,
![]() – приближенное значение аргумента
ответа в
– приближенное значение аргумента
ответа в
радианах,
![]() – приближенное значение аргумента
ответа в
– приближенное значение аргумента
ответа в
градусах.
Задача 5.б.
Вычислить значение многочлена
![]() при
при![]() .
.
а) Ответ записать в алгебраической форме;
б) найти точное значение модуля и его приближенное значение с точностью до 0,0001;
в) найти приближенное значение аргумента в радианах с точностью до 0,001 и в градусах с точностью до целого градуса.
![]() ,
,
![]() .
.
Решение.
Вычислим
![]() :
:
![]() ,
,
![]() .
.
Вычислим значение многочлена:
![]()
![]()
![]()
![]() .
.
Найдем модуль и
аргумент комплексного числа
![]() .
.
Так как
![]() ,
то
,
то![]() .
Имеем:
.
Имеем:
![]()
![]() ;
;
 ,
,
![]() ,
,
![]() .
.
Ответ: ![]()
![]() – алгебраическая форма,
– алгебраическая форма,
![]() – точное и приближенное значения
– точное и приближенное значения
модуля ответа,
![]() – приближенное значение аргумента
ответа в
– приближенное значение аргумента
ответа в
радианах,
![]() – приближенное значение аргумента
ответа в
– приближенное значение аргумента
ответа в
градусах.
Задача 6.а.
Вычислить значение функции
![]() при
при![]() .
Ответ записать в алгебраической форме.
Найти модуль и аргумент (в градусах)
ответа.
.
Ответ записать в алгебраической форме.
Найти модуль и аргумент (в градусах)
ответа.
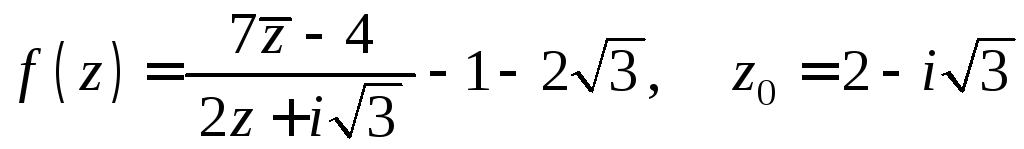 .
.
Решение. Имеем:
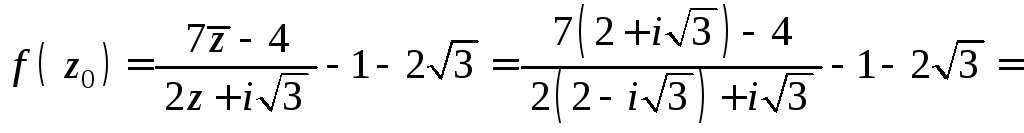



![]() .
.
Найдем модуль а
аргумент комплексного числа
![]() .
.
Так как
![]() ,
то
,
то![]() .
Имеем:
.
Имеем:
![]() ;
;
 ,
,
![]() .
.
Ответ: ![]() – алгебраическая форма,
– алгебраическая форма,
![]() – модуля ответа,
– модуля ответа,
![]() – значения аргумента ответа в градусах.
– значения аргумента ответа в градусах.
Задача 6.б.
Вычислить значение функции
![]() при
при![]() .
Ответ записать в алгебраической форме.
Найти модуль и аргумент (в градусах)
ответа.
.
Ответ записать в алгебраической форме.
Найти модуль и аргумент (в градусах)
ответа.
 .
.
Решение. Имеем:



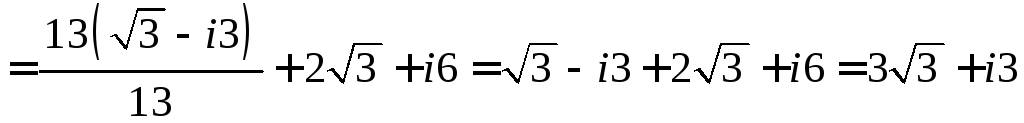 .
.
Найдем модуль и
аргумент комплексного числа
![]() .
.
Так как
![]() ,
то
,
то![]() .
Имеем:
.
Имеем:
![]() ;
;
 ,
,
![]() .
.
Ответ: ![]() – алгебраическая форма,
– алгебраическая форма,
![]() – модуля ответа,
– модуля ответа,
![]() – значения аргумента ответа в градусах.
– значения аргумента ответа в градусах.
Задача 7.а.
Вычислить значение функции
![]() при
при![]() .
.
а) Ответ записать в алгебраической форме;
б) найти точное значение модуля и его приближенное значение с точностью до 0,0001;
в) найти приближенное значение аргумента в радианах с точностью до 0,001 и в градусах с точностью до целого градуса.
 .
.
Решение.
Вычислим значения
![]() и
и![]() :
:
![]() ,
,
![]() ,
,
![]() .
.
Вычислим значение
![]() :
:
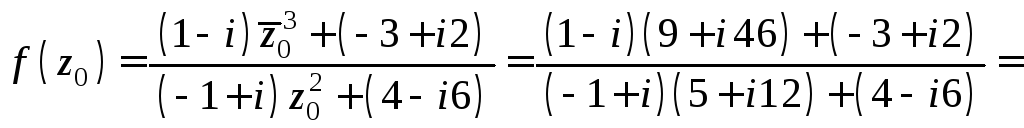
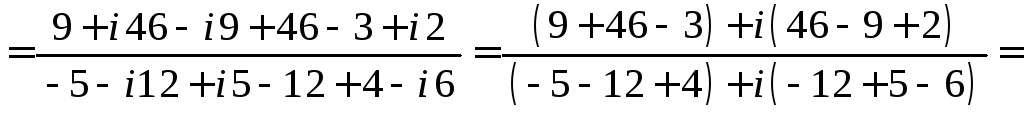
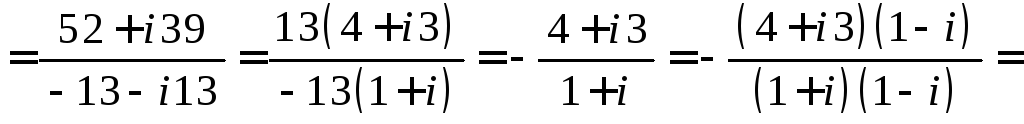
![]() .
.
Найдем модуль и
аргумент комплексного числа
![]() .
.
Так как
![]() ,
то
,
то![]() .
Имеем:
.
Имеем:

![]() ;
;
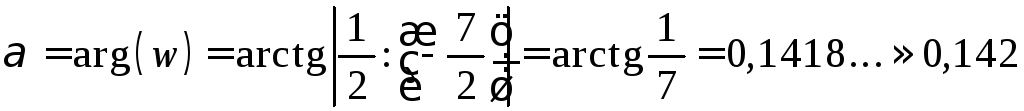 ,
,
![]() ,
,
![]() .
.
Ответ: ![]() – алгебраическая форма,
– алгебраическая форма,
 – точное и приближенное значения
– точное и приближенное значения
модуля ответа,
![]() – приближенное значение аргумента
ответа в
– приближенное значение аргумента
ответа в
радианах,
![]() – приближенное значение аргумента
ответа в
– приближенное значение аргумента
ответа в
градусах.
Задача 7.б.
Вычислить значение функции
![]() при
при![]() .
.
а) Ответ записать в алгебраической форме;
б) найти точное значение модуля и его приближенное значение с точностью до 0,0001;
в) найти приближенное значение аргумента в радианах с точностью до 0,001 и в градусах с точностью до целого градуса.
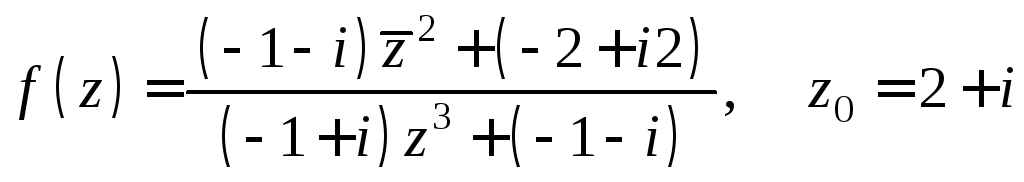 .
.
Решение.
Вычислим значения
![]() и
и![]() :
:
![]() ,
,
![]() ,
,
![]() .
.
Вычислим значение
![]() :
:



 .
.
Найдем модуль и
аргумент комплексного числа
![]() .
.
Так как
![]() ,
то
,
то![]() .
Имеем:
.
Имеем:
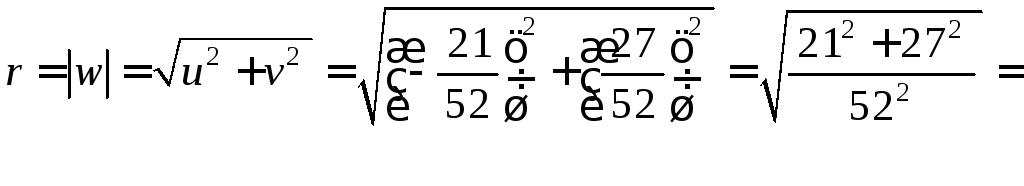
 ;
;
 ,
,
![]() ,
,
![]() .
.
Ответ: ![]() – алгебраическая форма,
– алгебраическая форма,
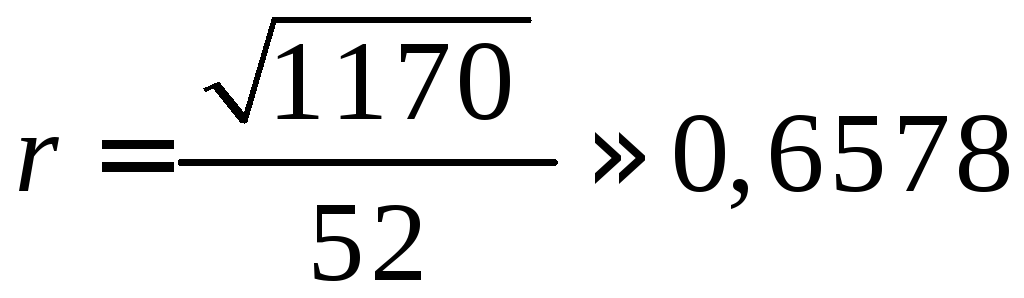 – точное и приближенное значения
– точное и приближенное значения
модуля ответа,
![]() – приближенное значение аргумента
ответа в
– приближенное значение аргумента
ответа в
радианах,
![]() – приближенное значение аргумента
ответа в
– приближенное значение аргумента
ответа в
градусах.
Задача 8.а. Решить данное линейное уравнение.
а) Ответ записать в алгебраической форме;
б) найти точное значение модуля и его приближенное значение с точностью до 0,0001;
в) найти приближенное значение аргумента в радианах с точностью до 0,001 и в целых градусах.
 .
.
Решение. Преобразуем вид данного уравнения:
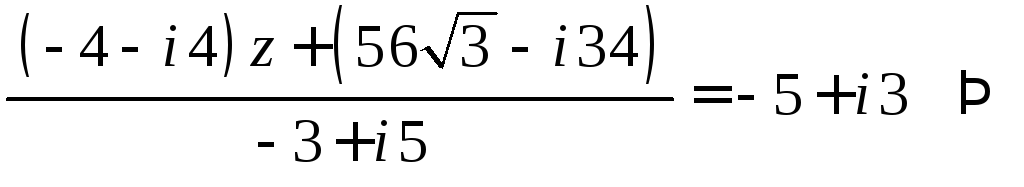
![]()
![]()
![]()
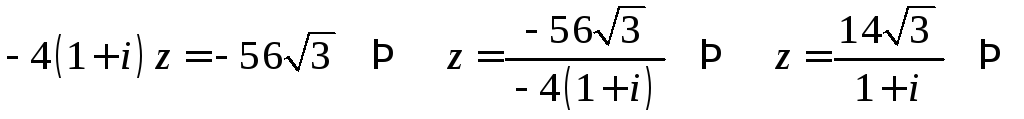
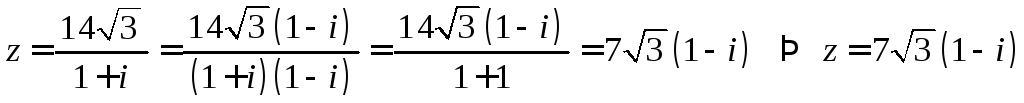 .
.
Найдем модуль и
аргумент комплексного числа
![]() .
.
Так как
![]() ,
то
,
то![]() .
Имеем:
.
Имеем:
![]() ;
;
![]() ;
;
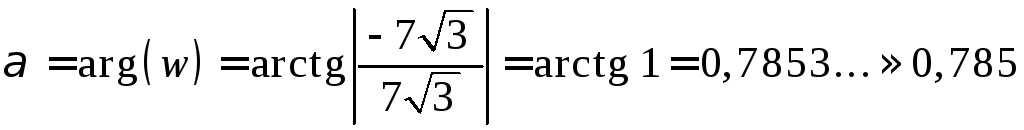 ,
,
![]() ,
,
![]() .
.
Ответ: ![]() – алгебраическая форма решения,
– алгебраическая форма решения,
![]() – точное и приближенное значения
– точное и приближенное значения
модуля решения,
![]() – приближенное значение аргумента
решения в
– приближенное значение аргумента
решения в
радианах,
![]() – точное значение аргумента решения в
градусах.
– точное значение аргумента решения в
градусах.
Задача 8.б. Решить данное линейное уравнение.
а) Ответ записать в алгебраической форме;
б) найти точное значение модуля и его приближенное значение с точностью до 0,0001;
в) найти приближенное значение аргумента в радианах с точностью до 0,001 и в целых градусах.
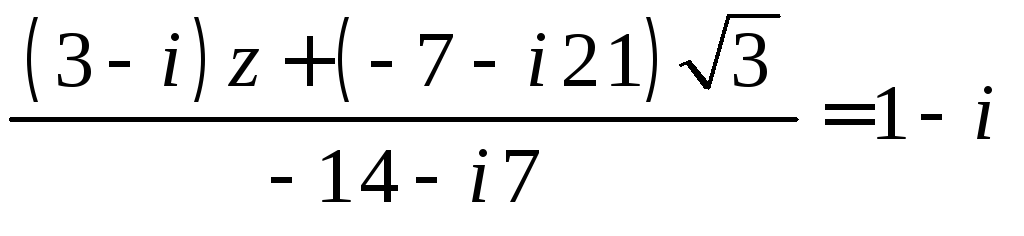 .
.
Решение. Преобразуем вид данного уравнения:
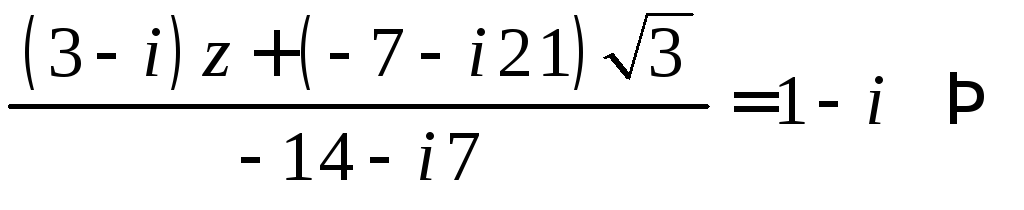
![]()
![]()
![]()
![]()
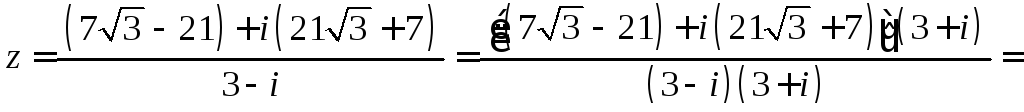
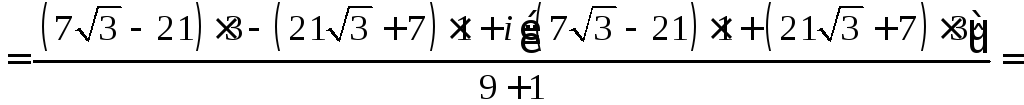
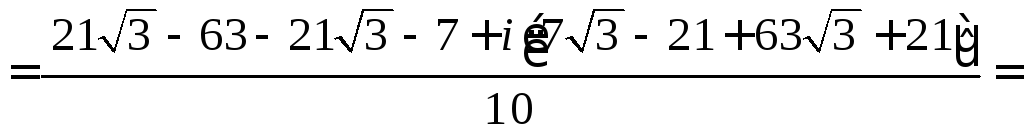
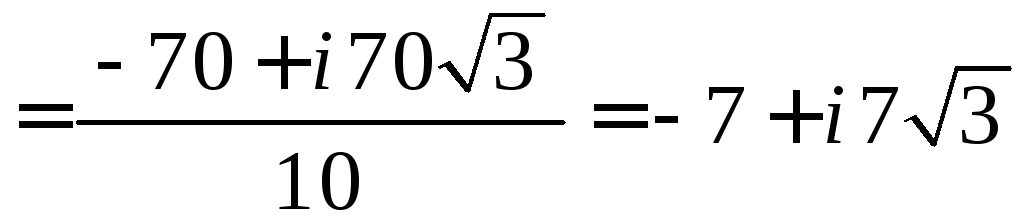 .
.
Найдем модуль и
аргумент комплексного числа
![]() .
.
Так как
![]() ,
то
,
то![]() .
Имеем:
.
Имеем:
![]() ;
;
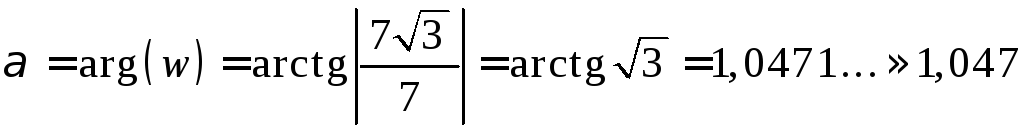 ,
,
![]() ,
,
![]() .
.
Ответ: ![]() – алгебраическая форма решения,
– алгебраическая форма решения,
![]() – точное значение модуля решения,
– точное значение модуля решения,
![]() – приближенное значение аргумента
решения в
– приближенное значение аргумента
решения в
радианах,
![]() – точное значение аргумента решения в
градусах.
– точное значение аргумента решения в
градусах.
Задача 9.а. Решить систему. Ответ записать в алгебраической форме.
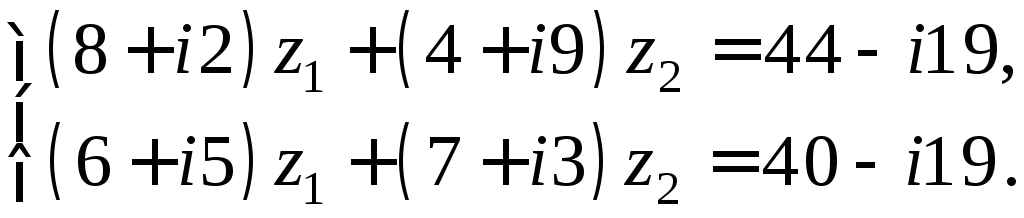
Решение. Решим систему методом Крамера. Вычислим основной и вспомогательные определители системы:
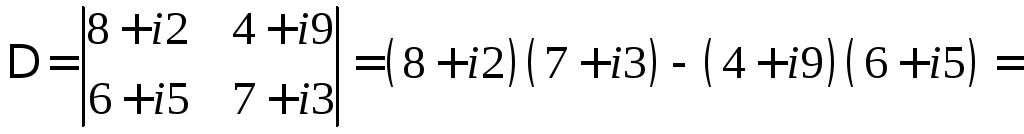
![]() ,
,
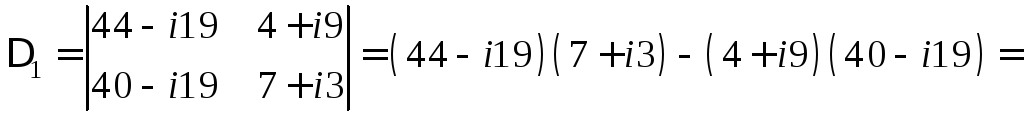
![]() ,
,
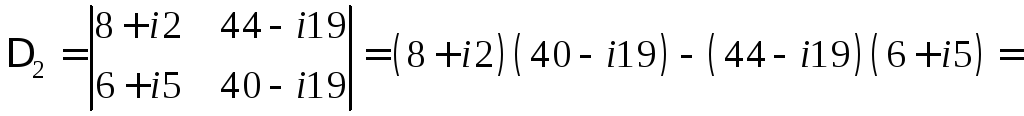
![]() .
.
Найдем решение по формулам Крамера:

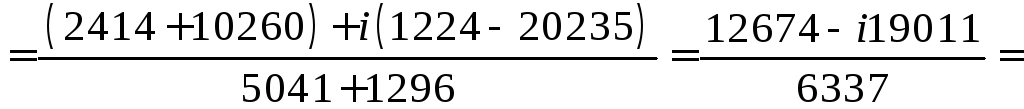
![]() ,
,
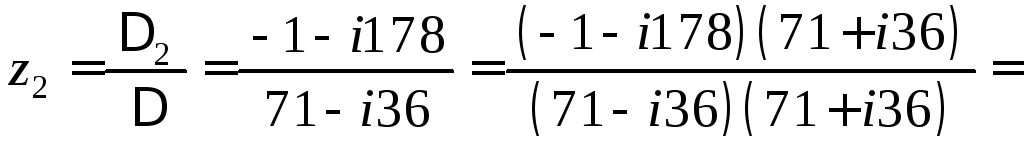
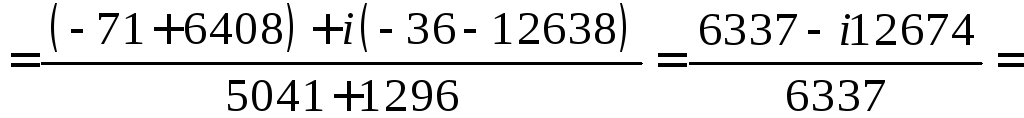
![]() .
.
Таким образом,
имеем
![]() .
.
Проверка:
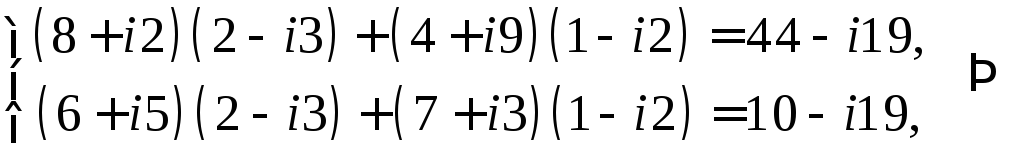
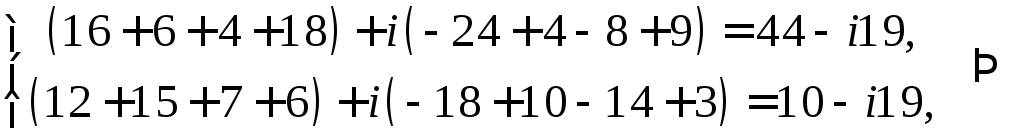
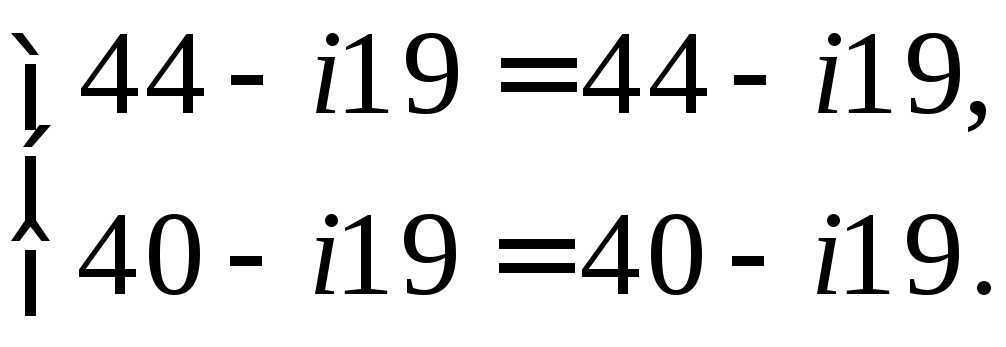
Ответ: 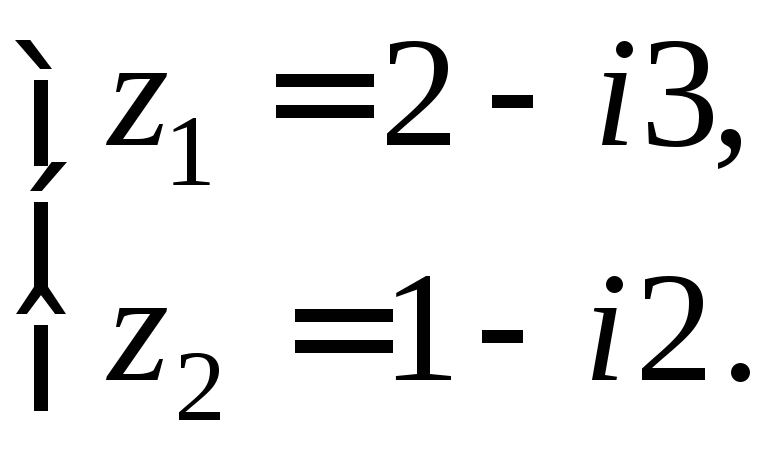
Задача 9.б. Решить систему. Ответ записать в алгебраической форме.
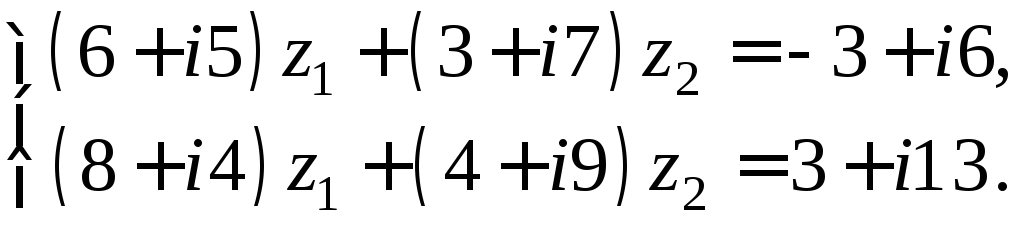
Решение.
Решим систему методом Гаусса (исключения
неизвестных). Для этого рядом с первым
уравнением запишем коэффициент при
![]() во втором уравнении, а рядом со вторым
уравнением запишем коэффициент при
во втором уравнении, а рядом со вторым
уравнением запишем коэффициент при![]() в первом уравнении. Умножим каждое
уравнение почленно на рядом стоящую
скобку, затем из первого равенства
вычтем второе. Тогда коэффициент при
в первом уравнении. Умножим каждое
уравнение почленно на рядом стоящую
скобку, затем из первого равенства
вычтем второе. Тогда коэффициент при![]() равняется нулю. Имеем:
равняется нулю. Имеем:

![]() ,
,

![]() ,
,

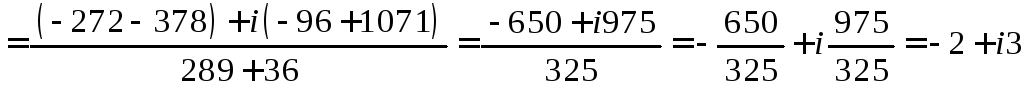 .
.
Подставим найденное
значение в первое уравнение и найдем
![]() :
:
![]() ,
,
![]() ,
,
![]() ,
,
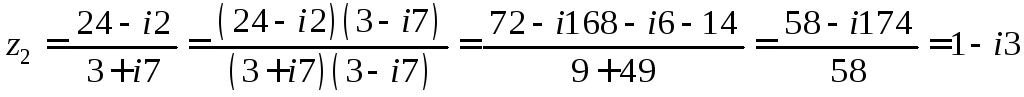 .
.
Таким образом,
имеем
![]() .
.
Проверка:

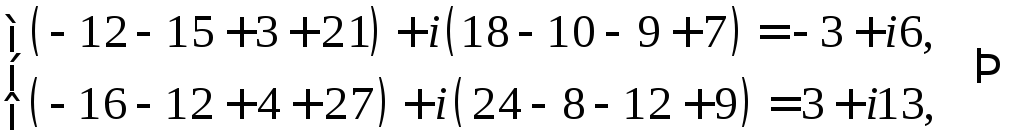

Ответ: 
Задача 10.а. Решить уравнение.
а) найти точное значение модуля и его приближенное значение с точностью до 0,001;
б) найти значение аргумента в целых градусах.
Значение
![]() указывается преподавателем.
указывается преподавателем.
![]()
Решение. Преобразуем данное уравнение:
![]()
![]()
![]()

 .
.
Найдем модуль и
аргумент комплексного числа
![]() .
.
Так как
![]() ,
то
,
то![]() .
Имеем:
.
Имеем:
![]() ;
;
 ,
,
![]() .
.
Воспользуемся
формулой для извлечения корня
![]() -й
степени
-й
степени
![]()
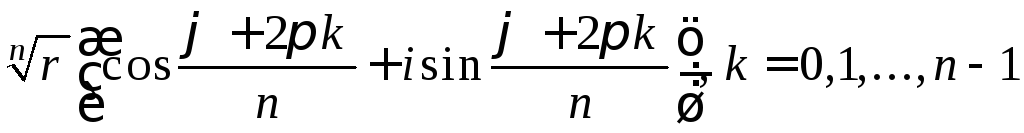 .
.
1) Если
![]() ,
то
,
то
![]()

![]()
![]() ;
;
![]() ,
,
![]() ,
,
![]() .
.
2) Если
![]() ,
то
,
то
![]()
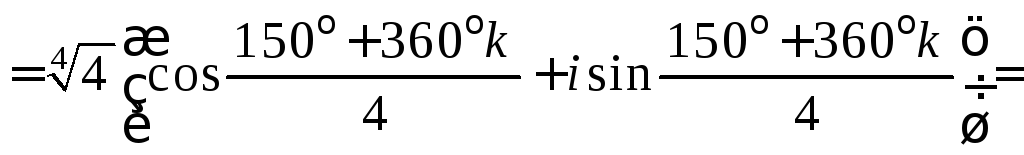
![]()
![]() ;
;
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
3) Если
![]() ,
то
,
то
![]()
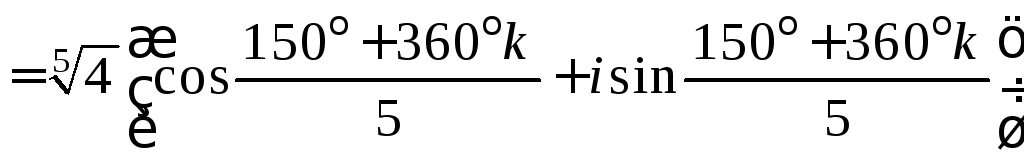
![]()
![]() ;
;
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
4) Если
![]() ,
то
,
то
![]()
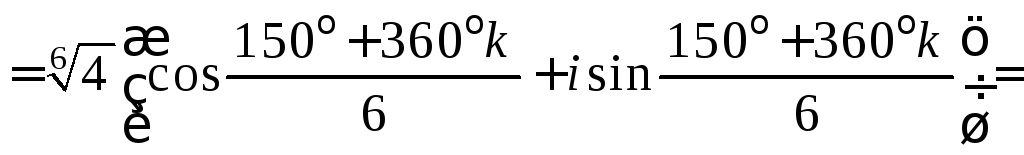
![]()
![]() ;
;
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Ответ: 1)
![]() .
.
2)
![]() .
.
3)
![]() ,
,
![]() .
.
4)
![]() ,
,
![]() .
.
Задача 10.б. Решить уравнение.
а) найти точное значение модуля и его приближенное значение с точностью до 0,001;
б) найти главное значение аргумента в целых градусах.
Значение
![]() указывается преподавателем.
указывается преподавателем.
![]()
Решение.
Умножим обе части уравнения на
![]() – сопряженному числу коэффициенту при
– сопряженному числу коэффициенту при
![]() и преобразуем полученное уравнение:
и преобразуем полученное уравнение:
![]()
![]()
![]()
![]()
![]() .
.
Найдем модуль и
аргумент комплексного числа
![]() .
.
Так как
![]() ,
то
,
то![]() .
Имеем:
.
Имеем:
![]() ,
,
![]() ;
;
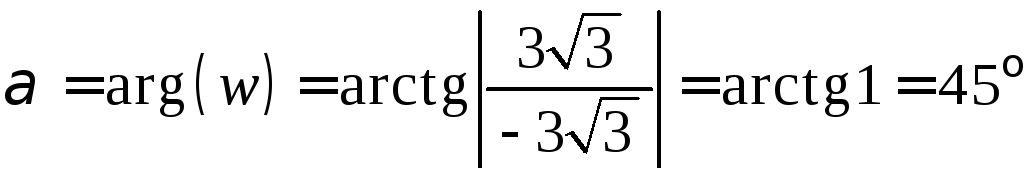 ,
,
![]() .
.
Воспользуемся
формулой для извлечения корня
![]() -й
степени
-й
степени
![]()
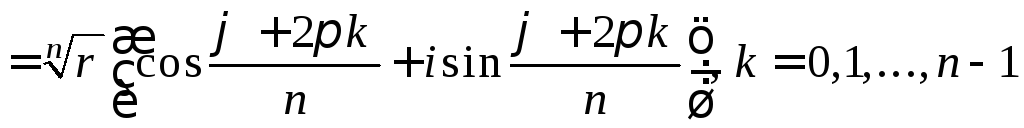 .
.
1) Если
![]() ,
то
,
то
![]()
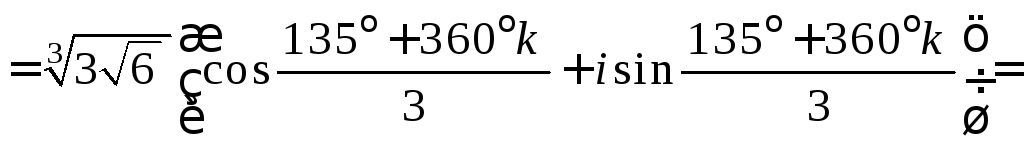
![]()
![]() .
.
Запишем тригонометрические формы корней со стандартными значениями аргументов:
![]() ,
,
![]() ,
,
![]() .
.
Запишем тригонометрические формы корней с главными значениями аргументов:
![]() ,
,
![]() ,
,
![]() .
.
2) Если
![]() ,
то
,
то
![]()
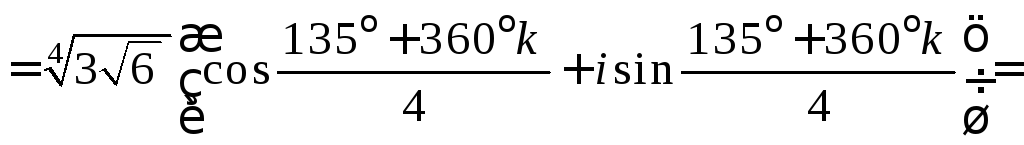
![]()
![]() .
.
Запишем тригонометрические формы корней со стандартными значениями аргументов:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Запишем тригонометрические формы корней с главными значениями аргументов:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
3) Если
![]() ,
то
,
то
![]()

![]()
![]() ;
;
Запишем тригонометрические формы корней со стандартными значениями аргументов:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Запишем тригонометрические формы корней с главными значениями аргументов:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
4) Если
![]() ,
то
,
то
![]()

![]()
![]() ;
;
Запишем тригонометрические формы корней со стандартными значениями аргументов:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Запишем тригонометрические формы корней с главными значениями аргументов:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Ответ: 1)
![]() .
.
2)
![]() .
.
3)
![]() ,
,
![]() .
.
4)
![]() ,
,
![]() .
.
Задача 11.а. Решить квадратное уравнение: а) найти алгебраической форму корней; б) найти модули и аргументы корней в градусах.
![]() .
.
Решение. Вычислим дискриминант данного квадратного уравнения:
![]() .
.
Представим полученное значение в виде:
![]() .
.
Так как
![]() ,
,
то приравнивая правые части последних двух равенств, получим систему двух уравнений
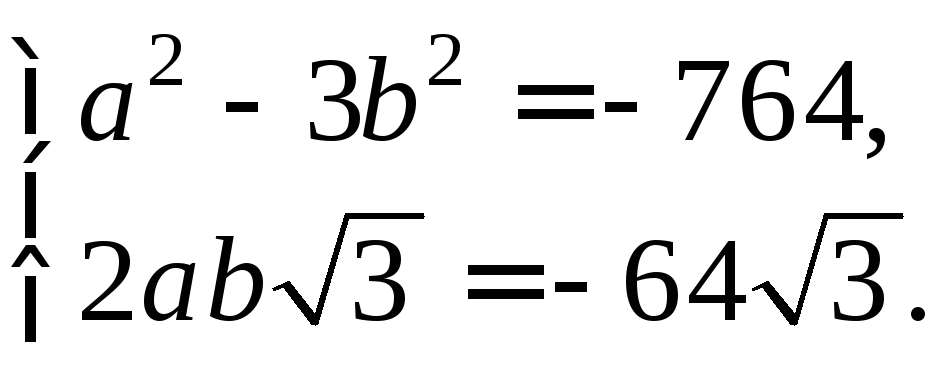
Решим полученную систему:

Подставим во второе
уравнение выражение для
![]() из первого уравнения и решим биквадратное
уравнение:
из первого уравнения и решим биквадратное
уравнение:
![]() ;
;
![]() ;
;
1)
![]() .
В этом случае биквадратное уравнение
не имеет корней;
.
В этом случае биквадратное уравнение
не имеет корней;
2)
![]() .
.
Подставляя значения
![]() в равенстве
в равенстве![]() ,
найдем значения
,
найдем значения![]() :
:
 .
.
Таким образом, имеем
![]() или
или
![]() .
.
Дальнейшее вычисление не зависит от того, какое из этих равенств нами будет использовано. так как в обоих случаях получим один и тот же ответ.
Найдем корни исходного квадратного уравнения:
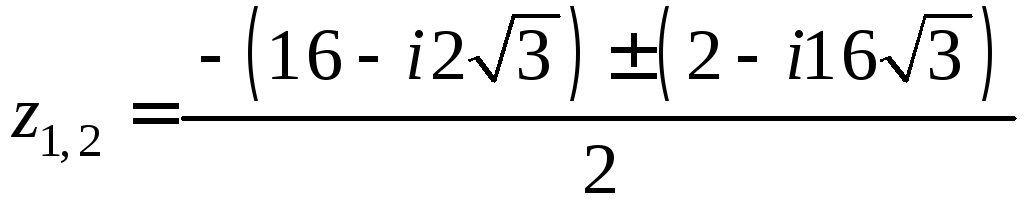 .
.
1)
 .
.
Найдем модуль и
аргумент комплексного числа
![]() :
:
![]() ;
;
![]() ,
,
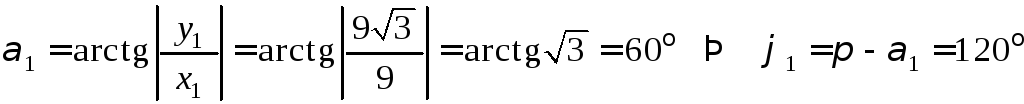 .
.
2)
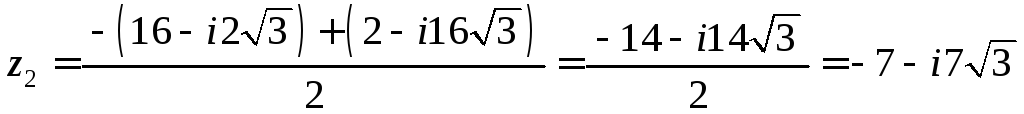 .
.
Найдем модуль и
аргумент комплексного числа
![]() :
:
![]() ;
;
![]() ,
,
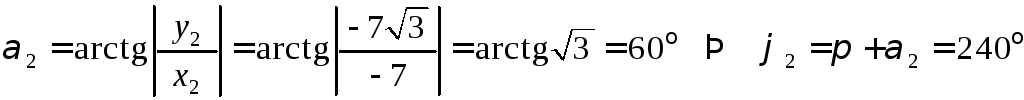 .
.
Ответ: ![]() ,
,![]() ,
,
![]() ;
;
![]() ,
,
![]() ,
,
![]() .
.
Задача 11.б. Решить квадратное уравнение: а) найти алгебраической форму корней; б) найти модули и аргументы корней в градусах.
![]() .
.
Решение. Вычислим дискриминант данного квадратного уравнения:
![]() .
.
Представим полученное значение в виде:
![]() .
.
Так как
![]() ,
,
то приравнивая правые части последних двух равенств, получим систему двух уравнений
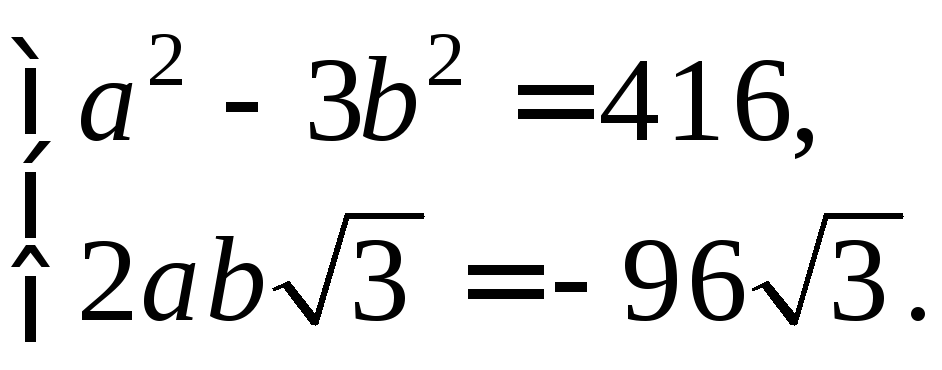
Решим полученную систему:

Подставим во второе
уравнение выражение для
![]() из первого уравнения и решим биквадратное
уравнение:
из первого уравнения и решим биквадратное
уравнение:
![]() ;
;
![]() ;
;
1)
![]() .
В этом случае биквадратное уравнение
не имеет корней;
.
В этом случае биквадратное уравнение
не имеет корней;
2)
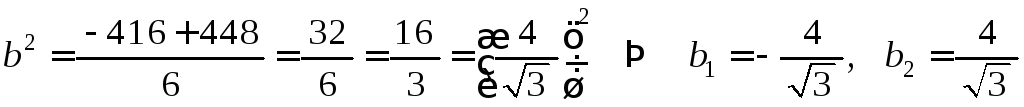 .
.
Подставляя значения
![]() в равенстве
в равенстве![]() ,
найдем значения
,
найдем значения![]() :
:
 .
.
Таким образом, имеем
![]() или
или
![]() .
.
Дальнейшее вычисление не зависит от того, какое из этих равенств нами будет использовано. так как в обоих случаях получим один и тот же ответ.
Найдем корни исходного квадратного уравнения:
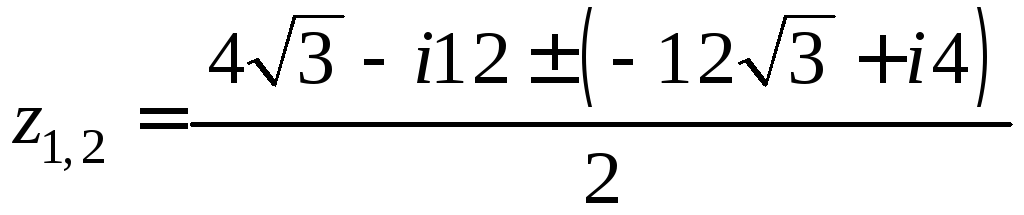 .
.
1)
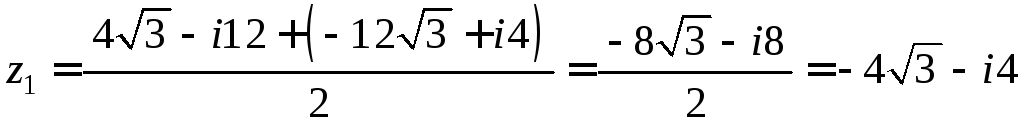 .
.
Найдем модуль и
аргумент комплексного числа
![]() :
:
![]() ;
;
![]() ,
,
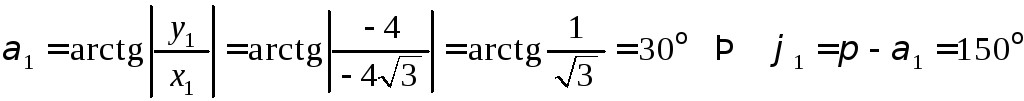 .
.
2)
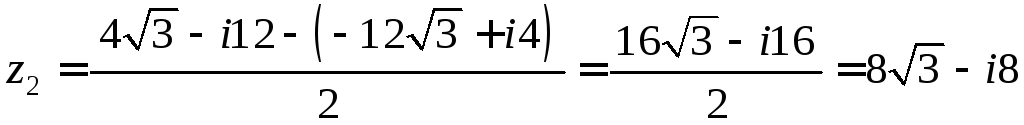 .
.
Найдем модуль и
аргумент комплексного числа
![]() :
:
![]() ;
;
![]() ,
,
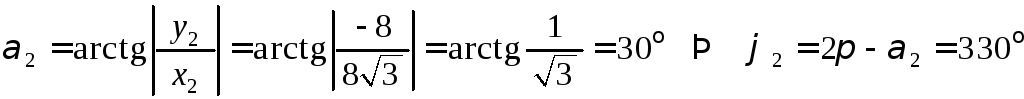 .
.
Ответ: ![]() ,
,![]() ,
,
![]() ;
;
![]() ,
,
![]() ,
,
![]() .
.
Задача 12.а. Решить кубическое уравнение: а) найти алгебраической форму корней; б) найти модули и аргументы корней в градусах.
![]() .
.
Указание. У данного уравнения имеется чисто мнимый корень.
Решение.
Согласно указанию у данного кубического
уравнения имеется чисто мнимый корень
![]() .
Так как
.
Так как![]() и
и![]() ,
то из данного уравнения будем иметь
,
то из данного уравнения будем иметь
![]()
![]()
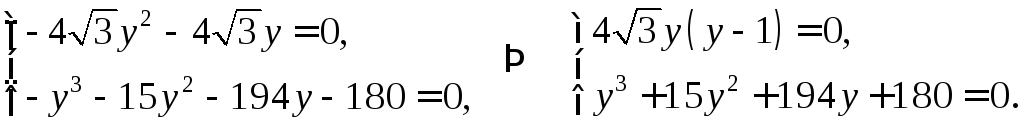
Из первого уравнения
системы находим: 1)
![]() ;
2)
;
2)![]() .
Подставим эти значения во второе
уравнение системы:
.
Подставим эти значения во второе
уравнение системы:
1)
![]() ;
;
следовательно,
![]() не является решением системы;
не является решением системы;
2)
![]()
![]()
следовательно,
![]() является решением системы.
является решением системы.
Таким образом,
![]() является корнем исходного кубического
уравнения:
является корнем исходного кубического
уравнения:![]() .
.
Найдем остальные корни. Для этого разложим левую часть на множители. Одним из множителей является линейный множитель:
![]() .
.
Второго множителя можно найти непосредственно:
![]()
![]() .
.
Решим квадратное
уравнение
![]() .
Вычислим его дискриминант:
.
Вычислим его дискриминант:
![]() .
.
Представим полученное значение в виде:
![]() .
.
Так как
![]() ,
,
то приравнивая правые части последних двух равенств, получим систему двух уравнений

Решим полученную систему:

Подставим во второе
уравнение выражение для
![]() из первого уравнения и решим биквадратное
уравнение:
из первого уравнения и решим биквадратное
уравнение:
![]() ;
;
![]() ;
;
1)
![]() .
В этом случае биквадратное уравнение
не имеет корней;
.
В этом случае биквадратное уравнение
не имеет корней;
2)
 .
.
Подставляя значения
![]() в равенстве
в равенстве![]() ,
найдем значения
,
найдем значения![]() :
:
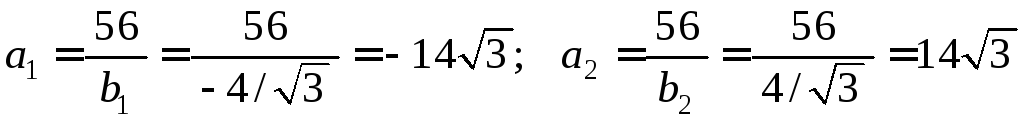 .
.
Таким образом, имеем
![]() или
или
![]() .
.
Дальнейшее вычисление не зависит от того, какое из этих равенств нами будет использовано. так как в обоих случаях получим один и тот же ответ.
Найдем корни квадратного уравнения:
 .
.
1)
 .
.
Найдем модуль и
аргумент комплексного числа
![]() :
:
![]() ;
;
![]() ,
,
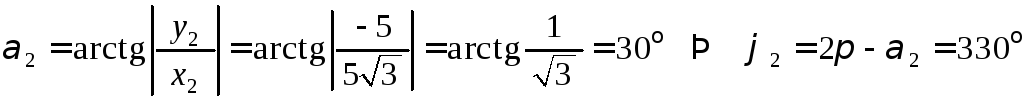 .
.
2)
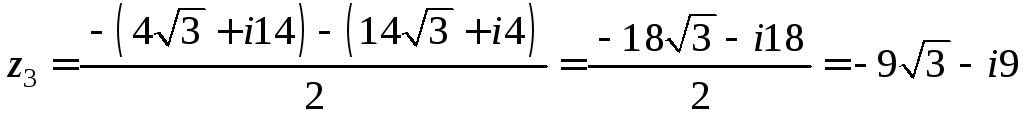 .
.
Найдем модуль и
аргумент комплексного числа
![]() :
:
![]() ;
;
![]() ,
,
 .
.
Ответ: ![]() ,
,![]() ,
,
![]() ;
;
![]() ,
,
![]() ,
,
![]() ;
;
![]() ,
,
![]() ,
,
![]() .
.
Задача 12.б. Решить кубическое уравнение: а) найти алгебраической форму корней; б) найти модули и аргументы корней в градусах.
![]() .
.
Указание. У данного уравнения имеется чисто мнимый корень.
Решение.
Согласно указанию у данного кубического
уравнения имеется чисто мнимый корень
![]() .
Так как
.
Так как![]() и
и![]() ,
то из данного уравнения будем иметь
,
то из данного уравнения будем иметь
![]()
![]()

Из первого уравнения
системы находим: 1)
![]() ;
2)
;
2)![]() .
Подставим эти значения во второе
уравнение системы:
.
Подставим эти значения во второе
уравнение системы:
1)
![]() ;
;
следовательно,
![]() не является решением системы;
не является решением системы;
2)
![]()
![]() ,
,
следовательно,
![]() является решением системы.
является решением системы.
Таким образом,
![]() является корнем исходного кубического
уравнения:
является корнем исходного кубического
уравнения:![]() .
.
Найдем остальные корни. Для этого разложим левую часть на множители. Одним из множителей является линейный множитель:
![]() .
.
Второго множителя можно найти непосредственно:
![]()
![]() .
.
Решим квадратное
уравнение
![]() .
Вычислим его дискриминант:
.
Вычислим его дискриминант:
![]() .
.
Представим полученное значение в виде:
![]() .
.
Так как
![]() ,
,
то приравнивая правые части последних двух равенств, получим систему двух уравнений
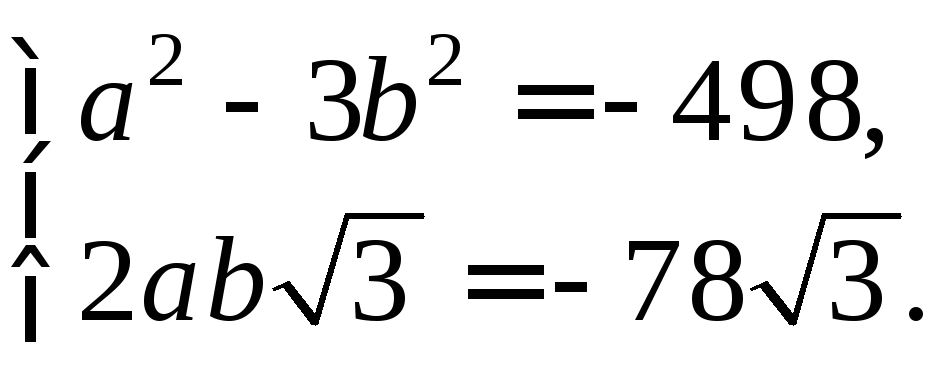
Решим полученную систему:
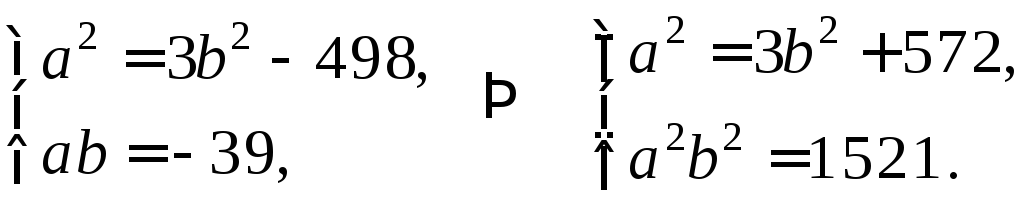
Подставим во второе
уравнение выражение для
![]() из первого уравнения и решим биквадратное
уравнение:
из первого уравнения и решим биквадратное
уравнение:
![]() ;
;
![]() ;
;
1)
![]() .
В этом случае биквадратное уравнение
не имеет корней;
.
В этом случае биквадратное уравнение
не имеет корней;
2)
![]() .
.
Подставляя значения
![]() в равенстве
в равенстве![]() ,
найдем значения
,
найдем значения![]() :
:
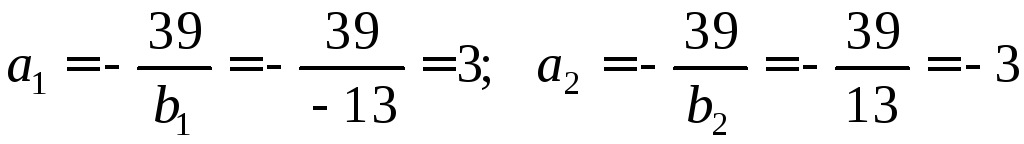 .
.
Таким образом, имеем
![]() или
или
![]() .
.
Дальнейшее вычисление не зависит от того, какое из этих равенств нами будет использовано. так как в обоих случаях получим один и тот же ответ.
Найдем корни квадратного уравнения:
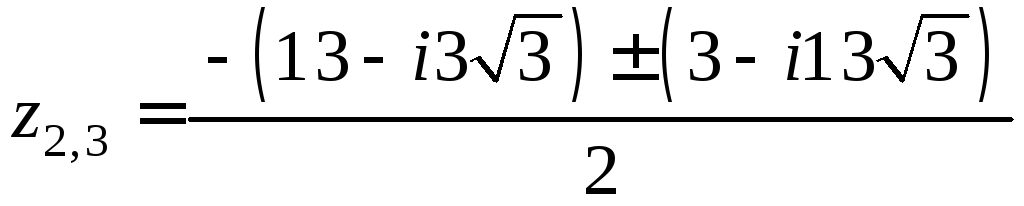 .
.
1)
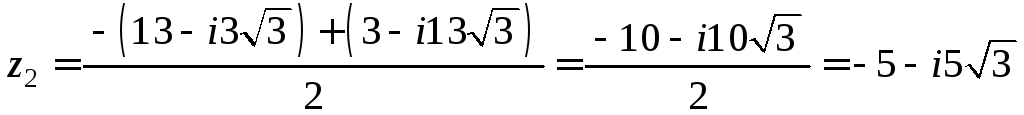 .
.
Найдем модуль и
аргумент комплексного числа
![]() :
:
![]() ;
;
![]() ,
,
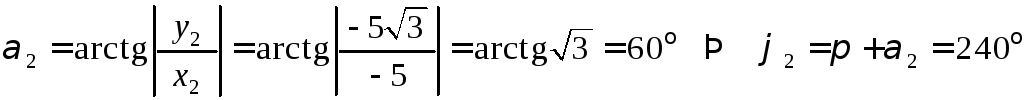 .
.
2)
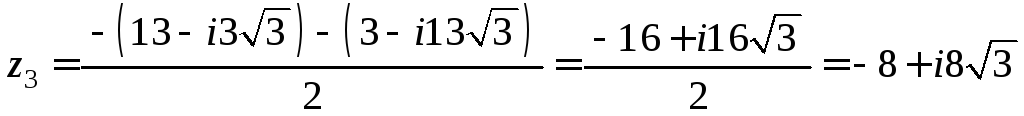 .
.
Найдем модуль и
аргумент комплексного числа
![]() :
:
![]() ;
;
![]() ,
,
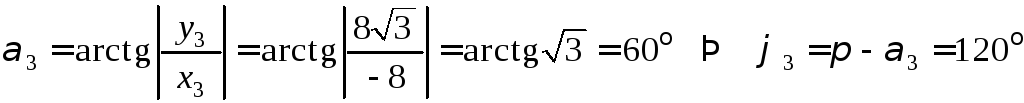 .
.
Ответ: ![]() ,
,
![]() ,
,
![]() ;
;
![]() ,
,
![]() ,
,
![]() ;
;
![]() ,
,
![]() ,
,
![]() .
.


