14

25.1 Нор­маль­ный скин-эф­фект, по­верх­но­ст­ный им­пе­данс ес­ли в ва­ку­у­ме вбли­зи про­во­дя­щей сре­ды су­ще­ст­ву­ет пе­ре­мен­ное элек­т­ро­маг­нит­ное по­ле, то оно про­ни­ка­ет в про­во­дя­щую сре­ду толь­ко на ко­не­ч­ную глу­би­ну. Это яв­ле­ние на­зы­ва­ет­ся скин-эф­фе­к­том. Наи­бо­лее про­с­то скин-эф­фект опи­сы­ва­ет­ся для ни­з­ко­ча­с­тот­ных по­лей бла­го­да­ря двум уп­ро­ща­ю­щим об­сто­я­тель­ст­вам. Во-пер­вых, ни­з­ко­ча­с­тот­ная во­л­на име­ет дли­ну , на­мно­го пре­вы­ша­ю­щую дли­ну l сво­бод­но­го про­бе­га но­си­те­лей то­ка в сре­де. При этом но­си­те­ли то­ка дви­жут­ся в по­ле, ко­то­рое, хо­тя и яв­ля­ет­ся пе­ре­мен­ным во вре­ме­ни, но мо­жет счи­тать­ся од­но­род­ным в про­стран­с­т­ве на рас­сто­я­ни­ях по­ряд­ка l. По­э­то­му связь то­ка с по­лем яв­ля­ет­ся ло­каль­ной ви­да j_i = _ikE_k, (1.40) , а про­стран­с­т­вен­ная ди­с­пер­сия не­су­ще­ст­вен­ной. Во-вто­рых, ес­ли раз­ме­ры L про­вод­ни­ка ма­лы в срав­не­нии с дли­ной во­л­ны элек­т­ро­маг­нит­ных ко­ле­ба­ний, то есть L <<  = 2c/, то на столь ни­з­ких ча­с­то­тах мо­ж­но пре­не­б­речь то­ком сме­ще­ния в урав­не­нии Мак­свел­ла (1.31) и за­пи­сать его для изо­троп­ной сре­ды с уче­том урав­не­ния (1.40) в ви­де rot H = 4E/c. (7.11) По­сколь­ку в про­вод­ни­ке на­ве­ден­ные по­лем за­ря­ды рас­са­сы­ва­ют­ся за вре­мя по­ряд­ка _р, то для ча­с­тот  <<  про­вод­ник мо­ж­но счи­тать ква­зи­нейт­раль­ным. В этом слу­чае урав­не­ние (1.10) ста­но­вит­ся од­но­род­ным: div E = 0. (7.12) Урав­не­ния (1.28) и (1.29) ос­та­ют­ся не­из­мен­ны­ми. Учи­ты­вая, что в урав­не­ние (1.39) при­ни­ма­ет вид В = Н, ис­к­лю­чим из урав­не­ний (1.28) и (7.11) с уче­том урав­не­ния (1.29)

25.2 име­ет­ся мно­жи­тель , обес­пе­чи­ва­ю­щий ло­ка­ли­за­цию по­ля в тон­ком слое вбли­зи по­верх­но­сти про­вод­ни­ка. Ха­ра­к­тер­ная тол­щи­на это­го скин-слоя . (7.19) Фор­му­ла (7.19) спра­ве­д­ли­ва, ес­ли вы­пол­ня­ют­ся ус­ло­вия l << , бла­го­да­ря че­му мо­ж­но пре­не­б­речь про­стран­с­т­вен­ной ди­с­пер­си­ей, и  << 1, где  – вре­мя сво­бод­но­го про­бе­га элек­т­ро­нов в ме­тал­ле, что по­з­во­ля­ет не учи­ты­вать вре­мен­ную ди­с­пер­сию и поль­зо­вать­ся ста­ти­че­с­кой про­во­ди­мо­стью . Из срав­не­ния урав­не­ний (7.13) и (7.14) вид­но, что маг­нит­ное по­ле в ме­тал­ле убы­ва­ет по то­му же за­ко­ну (7.18), что и элек­т­ри­че­с­кое. Най­дем со­от­но­ше­ние ме­ж­ду ве­ли­чи­на­ми на­пря­жен­но­стей элек­т­ри­че­с­ко­го и маг­нит­но­го по­лей на по­верх­но­сти про­вод­ни­ка. Из урав­не­ний (7.13) (7.18) и (7.19) сле­ду­ет, что ве­к­то­ры Е и Н свя­за­ны ме­ж­ду со­бой со­от­но­ше­ни­ем , (7.20) где n = k/k – еди­ни­ч­ный ве­к­тор, на­пра­в­лен­ный вдоль оси z. Со­от­но­ше­ние (7.20) спра­ве­д­ли­во для лю­бой то­ч­ки сре­ды и для по­верх­но­сти в том чи­с­ле. Ве­ли­чи­на

26.1 Ано­маль­ный скин-эф­фект Как сле­ду­ет из фор­му­лы (7.19), глу­би­на скин-слоя па­да­ет с ро­с­том ча­с­то­ты и про­во­ди­мо­сти сре­ды. Про­во­ди­мость же обы­ч­но про­пор­ци­о­наль­на дли­не сво­бод­но­го про­бе­га но­си­те­лей за­ря­да. По­э­то­му для чи­с­тых ме­тал­лов на до­с­та­то­ч­но вы­со­ких ча­с­то­тах или при ни­з­ких тем­пе­ра­ту­рах мо­жет ока­зать­ся, что  < l. В этом слу­чае элек­т­ро­ны дви­жут­ся в по­ле, ко­то­рое уже нель­зя счи­тать од­но­род­ным, и не­об­хо­ди­мо учи­ты­вать про­стран­с­т­вен­ную ди­с­пер­сию. Вре­мен­ная же ди­с­пер­сия при  < 1 еще не­су­ще­ст­вен­на. Скин-эф­фект в та­ких ус­ло­ви­ях на­зы­ва­ет­ся ано­маль­ным скин-эф­фе­к­том. В слу­чае ано­маль­но­го скин-эф­фе­к­та связь ме­ж­ду плот­но­стью на­ве­ден­но­го то­ка и на­пря­жен­но­стью элек­т­ри­че­с­ко­го по­ля пе­ре­ста­ет быть ло­каль­ной ви­да j_i = _ikE_k, (1.40) . Что­бы най­ти эту связь, за­пи­шем ли­не­а­ри­зо­ван­ное ки­не­ти­че­с­кое урав­не­ние ви­да (6.11) для функ­ции рас­пре­де­ле­ния элек­т­ро­нов в ме­тал­ле 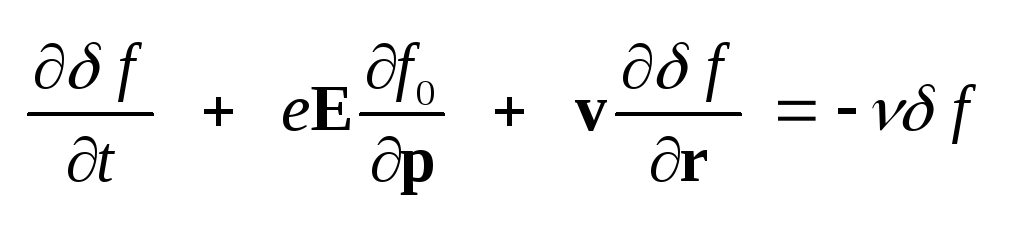, где f – обу­сло­в­лен­ное про­ни­ка­ю­щим в ме­талл по­лем от­кло­не­ние функ­ции рас­пре­де­ле­ния от рав­но­ве­с­ной фер­ми­ев­ской функ­ции f₀. Ес­ли во­л­на па­да­ет из ва­ку­у­ма на ме­талл в на­пра­в­ле­нии оси z, нор­маль­ной к по­верх­но­сти и на­пра­в­лен­ной вглубь ме­тал­ла, то Фу­рье-об­раз это­го урав­не­ния при­ни­ма­ет вид .

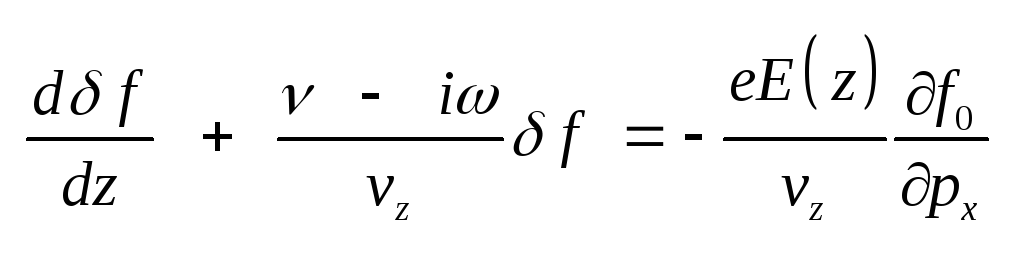26.2 Су­ще­ст­ву­ют два пре­дель­ных слу­чая – зер­каль­ное и диф­фуз­ное рас­се­я­ние. На пра­к­ти­ке ре­а­ли­зу­ет­ся не­ко­то­рая про­ме­жу­то­ч­ная си­ту­а­ция. Но да­же в са­мом про­с­том слу­чае зер­каль­но­го от­ра­же­ния элек­т­ро­нов от по­верх­но­сти уже про­яв­ля­ют­ся все ха­ра­к­тер­ные осо­бен­но­сти ано­маль­но­го скин-эф­фе­к­та. При зер­каль­ном рас­се­я­нии элек­т­ро­нов с уче­том фор­му­лы (7.25) по­лу­ча­ем: . Здесь функ­ция f⁽⁺⁾ от­но­сит­ся к элек­т­ро­нам, уда­ля­ю­щим­ся от по­верх­но­сти, а функ­ция f^(–) от­но­сит­ся к элек­т­ро­нам, при­бли­жа­ю­щим­ся к ней. Ин­те­грал в фор­му­ле (7.26) за­ви­сит толь­ко от ,  и v_z, по­э­то­му об­щее ре­ше­ние урав­не­ния (7.24) по ана­ло­гии с фор­му­лой (7.25) для уда­ля­ю­щих­ся от по­верх­но­сти элек­т­ро­нов, дол­ж­но иметь вид: . (7.26)

26.3 и (7.12) по­лу­чим c²E – ²E/t² = 4cj/t. Под­ста­в­ляя в Фу­рье-об­раз это­го урав­не­ния со­от­но­ше­ние (7.27), по­лу­чим в од­но­мер­ном слу­чае ос­нов­ное урав­не­ние ано­маль­но­го скин-эф­фе­к­та: 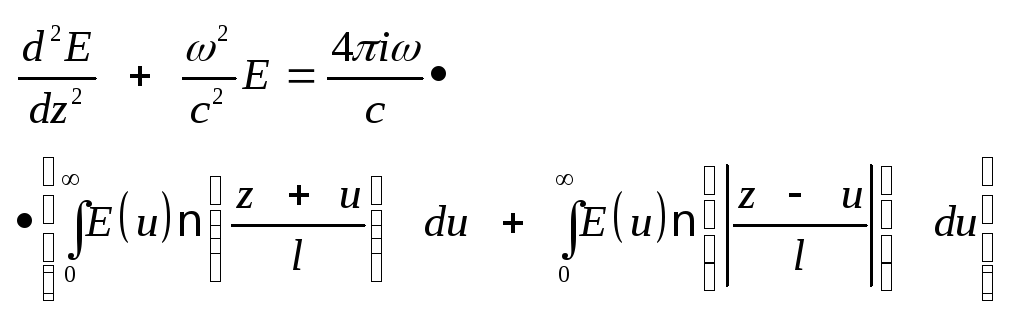, (7.29) оп­ре­де­ля­ю­щее по­ле в сре­де. Для ре­ше­ния ин­те­граль­но-диф­фе­рен­ци­аль­но­го урав­не­ния (7.29) сде­ла­ем во вто­ром ин­те­гра­ле в пра­вой ча­с­ти за­ме­ну пе­ре­мен­ных u  –u и про­дол­жим фор­маль­но ре­ше­ние E(z) в об­ласть z < 0 по пра­ви­лу E(–z) = E(z). То­г­да урав­не­ние (7.29) при­мет вид . (7.30) Урав­не­ние (7.30) име­ет раз­но­ст­ное яд­ро и его мо­ж­но ре­шить с по­мо­щью пре­об­ра­зо­ва­ния Фу­рье. Най­дем Фу­рье-об­раз урав­не­ния (7.30). Для это­го ум­но­жим его на exp(–ikz) и про­ин­тег­ри­ру­ем по z. В ле­вой ча­с­ти пер­вое сла­га­е­мое сле­ду­ет два­ж­ды про­ин­тег­ри­ро­вать по ча­с­тям и учесть, что для чет­ной по по­стро­е­нию функ­ции E(z) по­лу­ча­ем Е(–0) = –Е(+0). В ре­зуль­та­те по­лу­чим

27.1 Элек­т­ро­маг­нит­ные флу­к­ту­а­ции Рас­смо­т­рим вновь урав­не­ние . (1.8), опи­сы­ва­ю­щее клас­си­че­с­кую ди­на­ми­ку за­ря­дов в сре­де. Пер­вое сла­га­е­мое в пра­вой ча­с­ти урав­не­ния пред­ста­в­ля­ет со­бой по­ле­вой член, опи­сы­ва­ю­щий в об­щем слу­чае внеш­нее де­тер­ми­ни­ро­ван­ное воз­дей­ст­вие на си­с­те­му.. Вто­рое сла­га­е­мое, обо­з­на­чен­ное как сто­рон­няя не­элек­т­ро­маг­нит­ная си­ла f_e, опи­сы­ва­ет вза­и­мо­дей­ст­вие вы­де­лен­но­го за­ря­да со сре­дой. Это вза­и­мо­дей­ст­вие мо­жет быть, в свою оче­редь, раз­де­ле­но на три ча­с­ти: си­лу вя­з­ко­го тре­ния, про­пор­ци­о­наль­ную ско­ро­сти за­ря­да, уп­ру­гую, или воз­вра­ща­ю­щую, си­лу, про­пор­ци­о­наль­ную сме­ще­нию за­ря­да от по­ло­же­ния рав­но­ве­сия, и слу­чай­ную си­лу, опи­сы­ва­ю­щую бро­у­нов­ское дви­же­ние за­ря­дов. Ха­о­ти­че­с­кое дви­же­ние но­си­те­лей за­ря­да в от­сут­ст­вие ре­гу­ляр­но­го внеш­не­го воз­дей­ст­вия, по­ро­ж­да­ю­щее элек­т­ро­маг­нит­ные флу­к­ту­а­ции, яв­ля­ет­ся уни­вер­саль­ным свой­ст­вом сло­ж­ных си­с­тем, вы­те­ка­ю­щим из вто­ро­го на­ча­ла тер­мо­ди­на­ми­ки. Опи­са­ние этих флу­к­ту­а­ций с по­мо­щью фи­к­тив­ных слу­чай­ных сил, при­на­д­ле­жа­щее Лан­же­ве­ну, яв­ля­ет­ся од­ним из воз­мо­ж­ных и в не­ко­то­ром смы­с­ле по­доб­но вве­де­нию инер­ци­аль­ных сил (цен­т­ро­бе­ж­ной и ко­ри­о­ли­со­вой) в ме­ха­ни­ке. В та­кой тра­к­тов­ке урав­не­ние (1.8) в ли­ней­ном при­бли­же­нии при­ни­ма­ет вид урав­не­ния Лан­же­ве­на: . (7.34) Функ­ция F(t) в пра­вой ча­с­ти урав­не­ния (7.34) опи­сы­ва­ет де­тер­ми­ни­ро­ван­ное (ре­гу­ляр­ное) воз­дей­ст­вие на сре­ду, а функ­ция f(t) – слу­чай­ную си­лу, при­чем .

27.2 сле­ду­ет 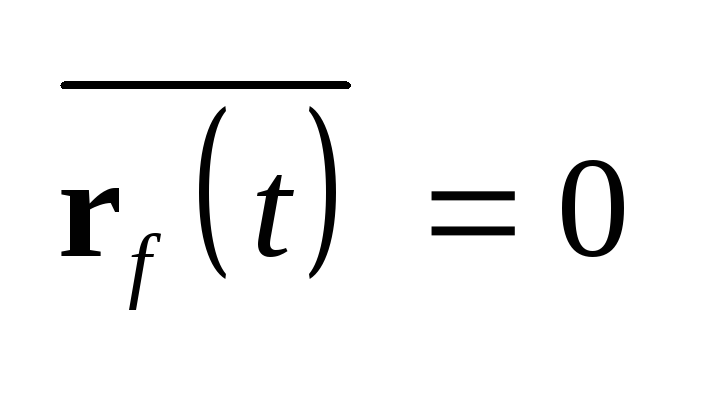, со­от­вет­ст­вен­но . Фу­рье-об­раз им­пульс­ной ха­ра­к­те­ри­сти­ки си­с­те­мы яв­ля­ет­ся ее ча­с­тот­ной ха­ра­к­те­ри­сти­кой . (7.39) Ча­с­тот­ная ха­ра­к­те­ри­сти­ка си­с­те­мы, ко­то­рую на­зы­ва­ют так­же обоб­щен­ной вос­при­им­чи­во­стью или за­па­з­ды­ва­ю­щей функ­ци­ей ли­ней­но­го от­кли­ка, яв­ля­ет­ся эр­ми­то­во со­пря­жен­ной, то есть H*(–) = H(). В свою оче­редь, . (7.40) Из из­ве­ст­ной те­о­ре­мы о свер­т­ке сле­ду­ет, что , где F() и r() – Фу­рье-об­ра­зы ви­да (7.39) внеш­ней си­лы и ве­к­то­ра сме­ще­ния. Из фор­мул (7.36), (7.37) и (7.39) сле­ду­ет, что 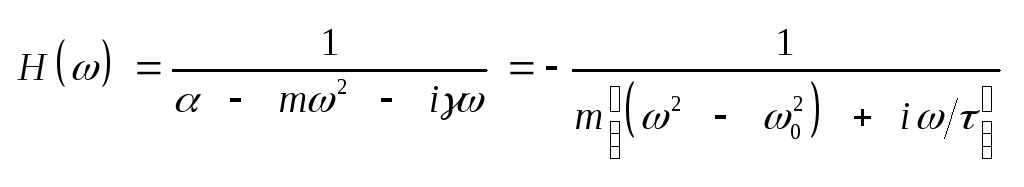, (7.41) где  = m/ – ха­ра­к­тер­ное вре­мя ре­ла­к­са­ции си­с­те­мы, – соб­ст­вен­ная (ре­зо­нанс­ная) ча­с­то­та си­с­те­мы.

27.3 (7.45) Для га­за сво­бод­ных элек­т­ро­нов (плаз­мы)  = 0, со­от­вет­ст­вен­но и ₀ = 0. То­г­да из фор­му­лы (7.43) сле­ду­ет, что . По­ла­гая в фор­му­ле (7.45) F = eE,  = 1/, по­лу­чим на вы­со­ких ча­с­то­тах  >>  ре­зуль­тат, сов­па­да­ю­щий с фор­му­лой (6.6). Рас­смо­т­рим те­перь сре­ду, на­хо­дя­щу­ю­ся в тер­мо­ди­на­ми­че­с­ком рав­но­ве­сии при тем­пе­ра­ту­ре Т, то есть F(t) = 0. В со­сто­я­нии рав­но­ве­сия в си­лу те­о­ре­мы о рав­но­рас­пре­де­ле­нии (эр­го­ди­че­с­кая ги­по­те­за) на ка­ж­дую сте­пень сво­бо­ды си­с­те­мы при­хо­дит­ся сред­няя энер­гия kT/2. Та­ким об­ра­зом, . С дру­гой сто­ро­ны, вхо­дя­щая в пра­вую часть урав­не­ния (7.34) лан­же­ве­нов­ская си­ла f(t) обу­сло­в­ле­на столк­но­ве­ни­я­ми но­си­те­лей за­ря­да, ко­то­рые в мас­шта­бе вре­ме­ни  яв­ля­ют­ся мгно­вен­ны­ми. Это зна­чит, что при ус­ред­не­нии по ма­к­ро­ско­пи­че­с­ко­му вре­ме­ни слу­чай­ную лан­же­ве­нов­скую си­лу мо­ж­но счи­тать дель­та-кор­ре­ли­ро­ван­ным про­цес­сом, то есть по­ло­жить

27.4 : . (7.50) Из фор­мул (7.46), (7.48) (7.50) и ус­ло­вия рав­но­рас­пре­де­ле­ния по­лу­ча­ем . (7.51) В свою оче­редь, из фор­мул (7.46), (7.48), (7.51) с уче­том со­от­но­ше­ний (7.41) и (7.43) сле­ду­ет фор­му­ла Кел­ле­на – Вель­то­на: 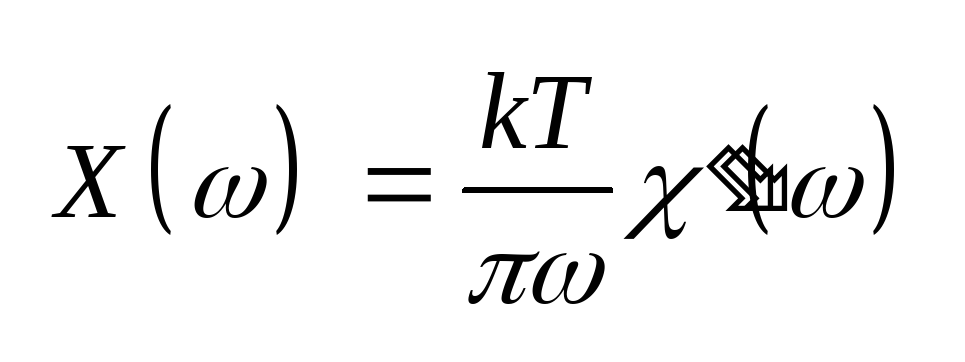, (7.52) свя­зы­ва­ю­щая флу­к­ту­а­ци­он­ные свой­ст­ва си­с­те­мы (спек­т­раль­ную ин­тен­сив­ность ее флу­к­ту­а­ций) с ее дис­си­па­тив­ны­ми свой­ст­ва­ми (мни­мой ча­стью обоб­щен­ной вос­при­им­чи­во­сти). Со­от­но­ше­ние (7.52) ча­с­то на­зы­ва­ет­ся флу­к­ту­а­ци­он­но-дис­си­па­ци­он­ной те­о­ре­мой. Флу­к­ту­а­ци­он­но-дис­си­па­ци­он­ная те­о­ре­ма (7.52) до­ка­за­на для мо­де­ли Дру­де – Ло­рен­ца, то есть си­с­те­мы, со­сто­я­щей из дис­крет­ных за­ря­дов с урав­не­ни­ем дви­же­ния ви­да (7.34). Фор­му­ла (4.42) яв­ля­ет­ся ча­ст­ным слу­ча­ем флу­к­ту­а­ци­он­но-дис­си­па­ци­он­ной те­о­ре­мы

28.1 Не­ли­ней­ная по­ля­ри­за­ция Ос­нов­ным свой­ст­вом ли­ней­ных ста­ци­о­нар­ных си­с­тем яв­ля­ет­ся гар­мо­ни­че­с­кий от­клик на гар­мо­ни­че­с­кое воз­дей­ст­вие. Од­на­ко, как сле­ду­ет из фор­му­лы 6.5, при уче­те си­лы Ло­рен­ца сво­бод­ный элек­т­рон под дей­ст­ви­ем гар­мо­ни­че­с­кой во­л­ны с ча­с­то­той  ис­пы­ты­ва­ет ко­ле­ба­ния с ча­с­то­той 2, про­доль­ные по от­но­ше­нию к во­л­но­во­му ве­к­то­ру k па­да­ю­щей во­л­ны: . По­э­то­му он и из­лу­ча­ет на ча­с­то­те 2, то есть про­ис­хо­дит ге­не­ра­ция вто­рой гар­мо­ни­ки элек­т­ро­маг­нит­ной во­л­ны. Под­ста­в­ляя по­лу­чен­ное ре­ше­ние для ко­ор­ди­на­ты z в х-про­ек­цию урав­не­ния (6.1) , по­лу­чим, что ко­ор­ди­на­та х бу­дет иметь со­ста­в­ля­ю­щую, со­от­вет­ст­ву­ю­щую ко­ле­ба­ни­ям на ча­с­то­те 3 и т. д. Та­ким об­ра­зом, уже в пер­вом по­ряд­ке ма­ло­сти по v/c газ сво­бод­ных элек­т­ро­нов об­ла­да­ет не­ли­ней­ной вос­при­им­чи­во­стью. В ре­аль­ной плаз­ме су­ще­ст­ву­ют и дру­гие ме­ха­низ­мы воз­ни­к­но­ве­ния не­ли­ней­но­сти. Не­ли­ней­ная по­ля­ри­за­ция, свя­зан­ная с ан­гар­мо­низ­мом ко­ле­ба­ний, воз­мо­ж­на в си­с­те­ме свя­зан­ных за­ря­дов, опи­сы­ва­е­мой мо­де­лью Дру­де – Ло­рен­ца (6.34). В ни­з­ко­ча­с­тот­ных по­лях не­ли­ней­ной вос­при­им­чи­во­стью об­ла­да­ют сег­не­то­э­лек­т­ри­ки и фер­ро­маг­не­ти­ки, как сле­ду­ет из фор­му­лы (4.61). В вы­со­ко­ча­с­тот­ных по­лях вос­при­им­чи­вость обы­ч­но счи­та­ет­ся ли­ней­ной. Это свя­за­но с тем, что вы­со­ко­ча­с­тот­ная по­ля­ри­за­ция обу­сло­в­ле­на дви­же­ни­ем элек­т­ро­нов в ато­мах. Кро­ме внеш­не­го по­ля на элек­т­рон при этом дей­ст­ву­ет соб­ст­вен­ное по­ле ато­ма по­ряд­ка Е₀ = 10⁹ В/см

28.2 (7.54) Ча­с­тот­ное пред­ста­в­ле­ние тен­зо­ра ли­ней­ной вос­при­им­чи­во­сти име­ет вид , (3.12) , то есть , (7.55) а для тен­зо­ров не­ли­ней­ной вос­при­им­чи­во­сти, со­от­вет­ст­вен­но , (7.56)

, (7.21) свя­зы­ва­ю­щая тан­ген­ци­аль­ные ком­по­нен­ты на­пря­жен­но­стей элек­т­ри­че­с­ко­го и маг­нит­но­го по­лей, на­зы­ва­ет­ся по­верх­но­ст­ным им­пе­дан­сом. На­пом­ним, что все пре­ды­ду­щие фор­му­лы бы­ли по­лу­че­ны для слу­чая нор­маль­но­го па­де­ния на гра­ни­цу сре­ды по­пе­ре­ч­ной во­л­ны. Вслед­ст­вие не­пре­рыв­но­сти тан­ген­ци­аль­ных ком­по­нент ве­к­то­ров по­ля на гра­ни­це сре­ды, со­от­но­ше­ние (7.20) спра­ве­д­ли­во и для по­лей на внеш­ней сто­ро­не про­вод­ни­ка. По­э­то­му со­от­но­ше­ние E_ = Z_S[H_  n] (7.22) мо­ж­но рас­сма­т­ри­вать как гра­ни­ч­ное ус­ло­вие, по­з­во­ля­ю­щее на­хо­дить по­ле вне про­вод­ни­ка, не рас­сма­т­ри­вая по­ле вну­т­ри сре­ды. В кур­се "Фи­зи­ка во­л­но­вых про­цес­сов" по­ка­зы­ва­ет­ся, что ус­ло­вие (7.22), на­зы­ва­е­мое гра­ни­ч­ным ус­ло­ви­ем Ле­он­то­ви­ча, спра­ве­д­ли­во не толь­ко для нор­маль­но­го па­де­ния во­л­ны на гра­ни­цу хо­ро­шо про­во­дя­щей сре­ды и да­же для не­пло­ской по­верх­но­сти, ес­ли ра­ди­ус ее кри­виз­ны ве­лик по срав­не­нию с ве­ли­чи­ной .

элек­т­ри­че­с­кое по­ле . (7.13) Ана­ло­ги­ч­но мо­ж­но ис­к­лю­чить маг­нит­ное по­ле с уче­том урав­не­ния (7.12): . (7.14) Пусть пло­ская гар­мо­ни­че­с­кая элек­т­ро­маг­нит­ная во­л­на па­да­ет нор­маль­но на по­верх­ность ме­тал­ла z > 0, так что элек­т­ри­че­с­кое по­ле име­ет толь­ко х-ком­по­нен­ту, а маг­нит­ное по­ле ­– толь­ко у-ком­по­нен­ту. Фу­рье-об­раз урав­не­ния (7.14) (7.15) име­ет ре­ше­ние E(z) = E₀ exp(kz). (7.16) Под­ста­в­ляя вы­ра­же­ние (7.16) в урав­не­ние (7.15), по­лу­чим: . (7.17) Та­ким об­ра­зом, ре­ше­ние урав­не­ния (7.14), опи­сы­ва­ю­щее элек­т­ро­маг­нит­ную во­л­ну в ме­тал­ле име­ет вид . (7.18) В этом ре­ше­нии сле­ду­ет со­хра­нить толь­ко сла­га­е­мое, об­ра­ща­ю­ще­е­ся на бес­ко­не­ч­но­сти в нуль. Та­ким об­ра­зом, кро­ме ос­цил­ли­ру­ю­щей ча­с­ти, в ре­ше­нии (7.18)

, (7.31) где . Ре­ше­ние ал­ге­б­ра­и­че­с­ко­го урав­не­ния (7.31) име­ет вид , ему со­от­вет­ст­ву­ет про­стран­с­т­вен­ное рас­пре­де­ле­ние по­ля . (7.32) Функ­ция E(z) в фор­му­ле (7.32) име­ет фи­зи­че­с­кий смысл при z > 0, мно­жи­тель Е(+0) оп­ре­де­ля­ет­ся ин­тен­сив­но­стью и дли­ной во­л­ны, па­да­ю­щей на по­верх­ность ме­тал­ла. Оцен­ка ин­те­гра­ла в фор­му­ле (7.32) да­ет, что глу­би­на про­ни­к­но­ве­ния элек­т­ро­маг­нит­но­го по­ля в ме­талл при ано­маль­ном скин-эф­фе­к­те име­ет по­ря­док . (7.33) Здесь E_F – энер­гия Фер­ми элек­т­ро­нов в ме­тал­ле. со­от­но­ше­ние (7.33) опи­сы­ва­ет убы­ва­ние глу­би­ны скин-слоя при ано­маль­ном скин-эф­фе­к­те как ^–1/3, то есть, ме­д­лен­нее, чем фор­му­ла (7.19) для нор­маль­но­го скин-эф­фе­к­та. Кро­ме то­го, функ­ция E(z) ви­да (7.32) убы­ва­ет с ро­с­том z не по экс­по­нен­ци­аль­но­му за­ко­ну (7.18), ха­ра­к­тер­но­му для нор­маль­но­го скин-эф­фе­к­та.

Вы­ра­же­ния (7.25) и (7.26) для функ­ции рас­пре­де­ле­ния по­з­во­ля­ют с по­мо­щью фор­му­лы ви­да , (6.13) най­ти плот­ность на­ве­ден­но­го то­ка j(z). Вво­дя в им­пульс­ном про­стран­с­т­ве по­ляр­ные ко­ор­ди­на­ты (v, , ), вы­брав по­ляр­ную ось вдоль оси х, то есть вдоль ве­к­то­ра Е, и вы­пол­няя ин­тег­ри­ро­ва­ние, по­лу­чим . (7.27) Здесь l = v – дли­на сво­бод­но­го про­бе­га элек­т­ро­нов, (7.28) яд­ро ин­те­граль­ной свя­зи ме­ж­ду на­пря­жен­но­стью элек­т­ри­че­с­ко­го по­ля в то­ч­ке с z-ко­ор­ди­на­той, рав­ной u, и плот­но­стью то­ка в про­из­воль­ной то­ч­ке z. Ин­те­граль­ный ха­ра­к­тер фор­му­лы (7.27) оз­на­ча­ет про­стран­с­т­вен­ную ди­с­пер­сию. Бу­дем рас­сма­т­ри­вать не­маг­нит­ный, то есть  = 1, В = Н, ме­талл без свя­зан­ных за­ря­дов, в ко­то­ром  = 1, D = E. Возь­мем ро­тор от урав­не­ния (1.28) и с уче­том урав­не­ний (1.31)

(7.23) Урав­не­ние (7.23), в ко­то­ром при­ня­то, что элек­т­ри­че­с­кое по­ле на­пра­в­ле­но вдоль оси х, удоб­но пе­ре­пи­сать в ви­де . (7.24) Ре­ше­ние не­од­но­род­но­го урав­не­ния (7.24) мо­ж­но ис­кать ме­то­дом ва­ри­а­ции по­сто­ян­ной в ви­де f = C(z)exp(–Az). Под­ста­нов­ка в урав­не­ние (7.24) да­ет, что ре­ше­ние, удо­в­ле­тво­ря­ю­щее гра­ни­ч­но­му ус­ло­вию f(z  , v_z < 0) = 0, име­ет вид . (7.25) Ус­ло­вие v_z < 0 в фор­му­ле (7.25) оз­на­ча­ет, что речь идет о функ­ции рас­пре­де­ле­ния элек­т­ро­нов, дви­жу­щих­ся по на­пра­в­ле­нию к по­верх­но­сти. Эта функ­ция оп­ре­де­ля­ет­ся зна­че­ни­ем элек­т­ри­че­с­ко­го по­ля во всем про­стран­с­т­ве от z до . Вид функ­ции f(z, v_z > 0), опи­сы­ва­ю­щей уда­ля­ю­щи­е­ся от гра­ни­цы элек­т­ро­ны, оп­ре­де­ля­ет­ся ха­ра­к­те­ром рас­се­я­ния элек­т­ро­нов на гра­ни­це.

. Слу­чай­ные про­цес­сы, функ­ция ав­то­кор­ре­ля­ции ко­то­рых за­ви­сит толь­ко от раз­но­сти мо­мен­тов вре­ме­ни, на­зы­ва­ет­ся ста­ци­о­нар­ны­ми. Рас­смо­т­рим спек­т­раль­ную ин­тен­сив­ность лан­же­ве­нов­ской си­лы, оп­ре­де­лен­ную как Фу­рье-об­раз ее функ­ции ав­то­кор­ре­ля­ции . (7.46) Слу­чай­ный про­цесс, спек­т­раль­ная ин­тен­сив­ность ко­то­ро­го по­сто­ян­на, на­зы­ва­ет­ся бе­лым шу­мом. Та­ким об­ра­зом, мо­ж­но рас­сма­т­ри­вать как ре­ак­цию ли­ней­ной си­с­те­мы (7.34) на бе­лый шум. Ана­ло­ги­ч­но со­от­но­ше­нию (7.46) мо­ж­но оп­ре­де­лить и спек­т­раль­ную ин­тен­сив­ность X() ста­ци­о­нар­ных элек­т­ро­маг­нит­ных флу­к­ту­а­ций x_f: . (7.47) В кур­се ста­ти­сти­че­с­кой ра­дио­фи­зи­ки до­ка­зы­ва­ет­ся, что спек­т­раль­ная ин­тен­сив­ность X() слу­чай­но­го про­цес­са на вы­хо­де ли­ней­ной си­с­те­мы с ча­с­тот­ной ха­ра­к­те­ри­сти­кой Н() свя­за­на со спек­т­раль­ной ин­тен­сив­но­стью G()слу­чай­но­го про­цес­са на вхо­де ли­ней­ной си­с­те­мы со­от­но­ше­ни­ем X() = |Н()|²G(). (7.48) С дру­гой сто­ро­ны, сред­ний ква­д­рат (мощ­ность) флу­к­ту­а­ций свя­зан с их спек­т­раль­ной ин­тен­сив­но­стью те­о­ре­мой Пар­се­ва­ля

Со­от­вет­ст­вен­но, , (7.42) . (7.43) Функ­ция Н(z), оп­ре­де­лен­ная фор­му­лой (7.41), яв­ля­ет­ся ана­ли­ти­че­с­кой в верх­ней ком­п­лекс­ной по­лу­пло­с­ко­сти Im(z) > 0. По­в­то­ряя рас­су­ж­де­ния, при­ве­ден­ные в п. 3.2, мо­ж­но по­ка­зать, что ее дей­ст­ви­тель­ная и мни­мая ча­с­ти удо­в­ле­тво­ря­ют со­от­но­ше­ни­ям Кра­мер­са – Кро­ни­га ви­да (3.23): , . (7.44) Как по­ка­за­но в п. 3.4, мни­мая часть обоб­щен­ной вос­при­им­чи­во­сти оп­ре­де­ля­ет мощ­ность, ко­то­рая по­гло­ща­ет­ся (дис­си­пи­ру­ет) си­с­те­мой. Дей­ст­ви­тель­но, пусть F(t) = F₀cos(t) = F₀[exp(it) + exp(–it)]/2. То­г­да для мощ­но­сти этой си­лы с уче­том фор­му­лы (7.38) по­лу­ча­ем

Ли­не­а­ри­за­ция урав­не­ния (7.34) под­ра­зу­ме­ва­ет не­за­ви­си­мость сил в пра­вой ча­с­ти от ко­ор­ди­нат и ско­ро­стей за­ря­дов. От­ме­тим, что в урав­не­нии (1.8) та­кая за­ви­си­мость уч­те­на. Об­щим свой­ст­вом ли­ней­ных си­с­тем яв­ля­ет­ся прин­цип су­пер­по­зи­ции, то есть, ре­ак­ция си­с­те­мы на сум­мар­ное воз­дей­ст­вие сил F(t) и f(t) рав­на сум­ме ре­ак­ций си­с­те­мы на эти си­лы по от­дель­но­сти. В свою оче­редь ре­ак­ция си­с­те­мы на си­лу F(t), F(t < 0) = 0 мо­жет быть пред­ста­в­ле­на в ви­де ин­те­гра­ла Дю­а­ме­ля . (7.35) Здесь – (7.36) им­пульс­ная ха­ра­к­те­ри­сти­ка (функ­ция Гри­на) си­с­те­мы, ­– (7.37) кор­ни ха­ра­к­те­ри­сти­че­с­ко­го урав­не­ния. Ес­ли в со­от­но­ше­нии (7.36) до­о­п­ре­де­лить h(t < 0) = 0, то урав­не­ние (7.35) мо­жет быть пе­ре­пи­са­но в ви­де . (7.38) Ре­ак­ция си­с­те­мы на слу­чай­ную си­лу f(t) так­же мо­жет быть за­пи­са­на в ви­де (7.38), при­чем из ус­ло­вия

. (7.57) Ква­д­ра­ти­ч­ная по­ля­ри­за­ция Р⁽²⁾ воз­мо­ж­на толь­ко в сре­дах без цен­т­ра ин­вер­сии. При на­ли­чии та­ко­го цен­т­ра за­ви­си­мость Р(Е) дол­ж­на быть не­чет­ной, и низ­щей не­ли­ней­ной по­ля­ри­за­ци­ей яв­ля­ет­ся ку­би­че­с­кая по­ля­ри­за­ция Р⁽³⁾. Не­ли­ней­ную по­ля­ри­за­цию вы­ше 3-го по­ряд­ка в ре­аль­ных за­да­чах не учи­ты­ва­ют. Ква­д­ра­ти­ч­ная по­ля­ри­за­ция сре­ды при­во­дит к ге­не­ра­ции вто­рой гар­мо­ни­ки, оп­ти­че­с­ко­му вы­пря­м­ле­нию, то есть к по­я­в­ле­нию по­сто­ян­ной со­ста­в­ля­ю­щей по­ля­ри­за­ции, а так­же к ли­ней­но­му элек­т­ро­оп­ти­че­с­ко­му эф­фе­к­ту Пок­кель­са, ли­ней­ная по­ля­ри­за­ция за­ви­сит от при­ло­жен­но­го к сре­де по­сто­ян­но­го элек­т­ри­че­с­ко­го по­ля. Ку­би­че­с­кая по­ля­ри­за­ция про­яв­ля­ет­ся в ква­д­ра­ти­ч­ном элек­т­ро­оп­ти­че­с­ком эф­фе­к­те Кер­ра, ко­ге­рент­ной ан­ти­сто­ксо­вом рас­се­я­нии и т. д. Эти яв­ле­ния рас­сма­т­ри­ва­ют­ся в кур­сах "Фи­зи­ка во­л­но­вых про­цес­сов" и "Кван­то­вая элек­т­ро­ни­ка".

Обы­ч­ные ис­то­ч­ни­ки вы­со­ко­ча­с­тот­но­го по­ля со­з­да­ют внеш­ние по­ля, на­пря­жен­ность ко­то­рых на мно­го по­ряд­ков мень­ше, чем Е₀. По­э­то­му су­ще­ст­ву­ет ма­лый па­ра­метр Е/Е₀, по ко­то­ро­му мо­ж­но раз­ло­жить ве­к­тор Р. Вви­ду край­ней ма­ло­сти это­го па­ра­ме­т­ра до­с­та­то­ч­но ог­ра­ни­чить­ся пер­вым сла­га­е­мым раз­ло­же­ния, то есть ли­ней­ной по­ля­ри­за­ци­ей. Един­ст­вен­ным ис­то­ч­ни­ком вы­со­ко­ча­с­тот­но­го элек­т­ро­маг­нит­но­го по­ля, на­пря­жен­ность при­бли­жа­ет­ся к ве­ли­чи­не Е₀, яв­ля­ет­ся ла­зер. По­э­то­му мо­ж­но ожи­дать, что в по­ле ла­зер­но­го лу­ча мо­гут по­я­вить­ся и вы­с­шие сла­га­е­мые раз­ло­же­ния ве­к­то­ра по­ля­ри­за­ции по сте­пе­ням па­ра­ме­т­ра Е/Е₀. В не­маг­нит­ных сре­дах мо­ж­но за­пи­сать . (7.53) Здесь P⁽ⁿ⁾ – сла­га­е­мое n-го по­ряд­ка по по­лю, – тен­зор тре­тье­го ран­га ква­д­ра­ти­ч­ной вос­при­им­чи­во­сти, – тен­зор чет­вер­то­го ран­га ку­би­че­с­кой вос­при­им­чи­во­сти и т. д. Про­стран­с­т­вен­ной ди­с­пер­си­ей не­ли­ней­ной по­ля­ри­за­ции ча­с­то пре­не­б­ре­га­ют. С уче­том ча­с­тот­ной ди­с­пер­сии, ко­то­рая обы­ч­но яв­ля­ет­ся су­ще­ст­вен­ной, ма­те­ри­аль­ные урав­не­ния сле­ду­ет за­пи­сы­вать в ви­де раз­ло­же­ния по ли­ней­ной, ква­д­ра­ти­ч­ной, ку­би­че­с­кой и т. д. по­ля­ри­за­ци­ям: